Skip to main content
SpringerLink
Log in

Determination of nonstationary temperature fields and stresses in piecewise homogeneous circular plates on the basis of a numerical-analytic Laplace inversion formula

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

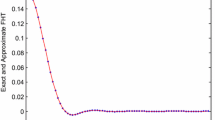
We investigate nonstationary temperature fields and stresses generated by them in piecewise homogeneous annular plates. An algorithm for the solution of the problem is based on the direct calculation of the Laplace transform and a modified Prudnikov formula for its inversion.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. H. S. Carslaw and J. C. Jaeger, Conduction of Heat in Solids, Oxford University Press, London (1959).

    Google Scholar 

  2. R. M. Kushnir, V. M. Maksymovych, and T. Ya. Solyar, “Determination of nonstationary temperatures with the help of improved formulas of the inverse Laplace transformation,” Fiz.-Khim Mekh. Mater., 38, No. 2, 18–26 (2002).

    Google Scholar 

  3. Ya. S. Podstrigach and Yu. M. Kolyano, Nonstationary Temperature Fields and Stresses in Thin Plates [in Russian], Naukova Dumka, Kiev (1972).

    Google Scholar 

  4. R. G. Campos and F. M. Díaz, “Quadrature formulas for the Laplace and Mellin transform analytic-element method for transient porous-media flow,” BIT Numer. Math., 49, No. 3, 477–486 (2009).

    Article  MATH  Google Scholar 

  5. B. Davis and B. Martin, “Numerical inversion of the Laplace transform: survey and comparison of methods,” J. Comput. Phys., 33, No. 1, 1–32 (1979).

    Article  MathSciNet  Google Scholar 

  6. K. L. Kuhlman and S. P. Neuman, “Laplace-transform analytic-element method for transient porous-media flow,” J. Eng. Math., 64, No. 2, 113–130 (2009).

    Article  MATH  MathSciNet  Google Scholar 

  7. M. Levesque, M. D. Gilchrist, N. Bouleau, K. Derrien, and D. Baptiste, “Numerical inversion of the Laplace–Carson transform applied to homogenization of randomly reinforced linear viscoelastic media,” Comput. Mech., 40, No. 4, 771–789 (2007).

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Pidstryhach Institute for Applied Problems in Mechanics and Mathematics, Ukrainian National Academy of Sciences, Lviv, Ukraine

    T. Ya. Solyar

Authors
  1. T. Ya. Solyar
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Matematychni Metody ta Fizyko-Mekhanichni Polya, Vol. 52, No. 3, pp. 201–208, July–September, 2009.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Solyar, T.Y. Determination of nonstationary temperature fields and stresses in piecewise homogeneous circular plates on the basis of a numerical-analytic Laplace inversion formula. J Math Sci 171, 673–681 (2010). https://doi.org/10.1007/s10958-010-0166-9

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-010-0166-9

Keywords

Search

Navigation