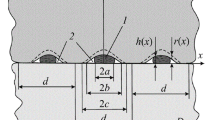
A model of contact between an elastic half space and a rigid base with a shallow surface rectangular hole is proposed. The hole contains an incompressible liquid and gas. The liquid occupies the middle part of the hole and forms a capillary bridge between the opposite surfaces. The remaining volume of the hole is filled with gas under a constant pressure. The liquid completely wets the surfaces of the bodies. The pressure drop at the liquid–gas interface caused by the surface tension is defined by the Laplace formula. The corresponding plane contact problem for the elastic half space is essentially nonlinear because the pressure of the liquid and the length of the capillary in the contact-boundary conditions are not known in advance and depend on the external load. The problem is reduced to a system of three equations (a singular integral equation for the function of height of the hole and two transcendental equations for the length of the capillary and the height of the meniscus). An analytic-numerical procedure for the solution of these equations is proposed. Dependences of the length of the capillary and the pressure drop at the liquid–gas interface on the external load, volume of liquid, and its surface tension are analyzed.
Similar content being viewed by others
References
S. A. Artsybyshev, Course in Physics. Part 1. Mechanics and Heat [in Russian], Ministerstvo Prosveshcheniya RSFSR, Moscow (1951).
I. G. Goryacheva and Yu. Yu. Makhovskaya, “Adhesive interaction of elastic bodies,” Prikl. Mat. Mekh., 65, No. 2, 279–289 (2001).
I. G. Goryacheva and Yu. Yu. Makhovskaya, “Contact of elastic bodies in the presence of capillary adhesion,” Prikl. Mat. Mekh., 63, No. 1, 128–137 (1999).
G. S. Kit, R. M. Martynyak, and I. M. Machishin, “Influence of a gas-liquid filler of an intercontact space on the stressed state of mating bodies,” Prikl. Mekh., 39, No. 3, 52–60 (2003).
R. M. Martynyak, “Contact of a half space with not plane base in the case of an intercontact gap filled with ideal gas,” Mat. Met. Fiz.-Mekh. Polya, 41, No. 4, 144–149 (1998).
R. M. Martynyak, “Contact interaction of two half spaces in the presence of a surface hole partially filled with incompressible liquid,” Fiz.-Khim. Mekh. Mater., 26, No. 2, 91–94 (1990).
R. M. Martynyak, “Mechanothermodiffusion interaction of bodies with regard for a filler of intercontact gaps,” Fiz.-Khim. Mekh. Mater., 36, No. 2, 124–126 (2000).
R. M. Martynyak, Thermoelastic Interaction in the Case of a Nonideal and Mechanical Contact [in Ukrainian], Candidate-Degree Thesis (Physics and Mathematics), Lviv (1987).
R. M. Martynyak and B. S. Slobodyan, “Interaction of two bodies in the presence of capillaries in an intercontact gap,” Mat. Met. Fiz.-Mekh. Polya, 49, No. 1, 164–173 (2006).
B. E. Monastyrs’kyi, “Influence of a filler of an intersurface gap on the interaction of bodies under conditions of nonideal contact,” Prikl. Probl. Mekh. Mat., Issue 1, 78–82 (2003).
N. I. Muskhelishvili, Some Main Problems of the Mathematical Theory of Elasticity [in Russian], Academy of Sciences of the USSR, Moscow (1954).
B. S. Slobodyan and R. M. Martynyak, “Simulation of interaction of bodies with regard for the surface tension of liquid in an intercontact gap,” Fiz.-Mat. Model. Inform. Tekhnol., 6, 19–29 (2007).
O. G. Chekina, “On the friction of rough surfaces separated by a thin layer of liquid,” Tren. Iznos, 19, No. 3, 306–311 (1998).
S. A. Chizhik, “Capillary mechanism of adhesion and friction of rough surfaces separated by a thin layer of liquid,” Tren. Iznos, 15, No. 1, 11–26 (1994).
Y. Ando, “Effect of capillary formation on friction and pull-off forces measured on submicron-size asperities,” Tribology Lett., 19, No. 1, 29–36 (2005).
Z. Dai, Y. Min, and S. Gorb, “Frictional characteristics of the beetle head-joint material,” Wear, 260, 168–174 (2006).
T. Kato, S. Watanabe, and H. Matsuoka, “Dynamic characteristics of an in-contact headslider considering meniscus force. Part 1. Formulation and application to the disk with sinusoidal undulation,” J. Tribology, 122, 633–638 (2000).
T. Kato, S. Watanabe, and H. Matsuoka, “Dynamic characteristics of an in-contact headslider considering meniscus force. Part 2. Application to the disk with random undulation and design conditions,” J. Tribology, 123, 168–174 (2001).
S. Kobatake, Y. Kawakubo, and S. Suzuki, “Laplace pressure measurement on laser textured thin-film disk,” Tribology Int., 36, 329–333 (2003).
P. Lambert and A. Delchambre, “Parameters ruling capillary force at the submillimetric scale,” Langmuir, 21, No. 21, 9537–9543 (2005).
Li Shi and M. Arunava, “Thermal transport mechanisms at nanoscale point contacts,” J. Heat Transfer., 124, 329–337 (2002).
C. Pailler-Mattei and H. Zahouani, “Analysis of adhesive behaviour of human skin in vivo by an indentation test,” Tribology Int., 39, No. 1, 12–21 (2006).
W. Peng and B. Bhushan, “Sliding contact analysis of layered elastic/plastic solids with rough surfaces,” Trans. ASME. J. Tribology, 124, 46–61 (2002).
Y. Rabinovich, M. Esayanur, and B. Moudgil, “Capillary forces between two spheres with a fixed volume liquid bridge: theory and experiment,” Langmuir, 21, 10992–10997 (2005).
A. Rennie, P. Dickrell, and W. Sawyer, “Friction coefficient of soft contact lenses: measurements and modeling,” Tribology Lett., 18, No. 4, 499–504 (2005).
F. Soulie, F. Cherblanc, M. El Youssoufi, and C. Saix, “Influence of liquid bridges on the mechanical behaviour of polydisperse granular materials,” Int. J. Numer. Anal. Meth. Geomech., 30, 123–228 (2006)
J. Zheng and J. L. Streutor, “A liquid bridge between two elastic half-spaces: A theoretical study of interface instability,” Tribology Lett., 16, Nos. 1–2, 1–9 (2004).
Author information
Authors and Affiliations
Additional information
Translated from Matematychni Metody ta Fizyko-Mekhanichni Polya, Vol. 51, No. 1, pp. 150–156, January–March, 2008.
Rights and permissions
About this article
Cite this article
Martynyak, R.M., Slobodyan, B.S. & Zelenyak, V.M. Pressure of an elastic half space on a rigid base with rectangular hole in the case of a liquid bridge between them. J Math Sci 160, 470–477 (2009). https://doi.org/10.1007/s10958-009-9511-2
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-009-9511-2