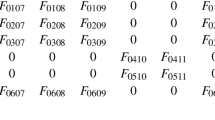Skip to main content
SpringerLink
Log in

Differentiation of tensor functions of the state of a body with regard for rotation

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

We consider the general representation of a tensor function of the state of anisotropic materials in the Euclidean space when the parameters of anisotropy are variable tensors of an arbitrary rank. Based on the generalizations of orthogonal and antisymmetric tensors of higher ranks, we write the equation of the tensor structure of a rotational function of arbitrary rank and the rule for its differentiation in direct (componentless) form. These relations can be used in the problems of the nonlinear mechanics of deformable solids concerning the influence of residual stresses on disturbances of an arbitrary nature in an anisotropic deformable solid.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. S. K. Godunov and T. Yu. Mikhailova, Representations of Rotational Groups and Spherical Functions [in Russian], Nauchnaya Kniga, Novosibirsk (1998).

    Google Scholar 

  2. A. Green and J. Adkins, Large Elastic Deformations and Non-Linear Continuum Mechanics, Clarendon, Oxford (1962).

    Google Scholar 

  3. Mechanics of Coupled Fields in Structural Elements [in Russian], Vol. 3: A. N. Guz’ and F. G. Makhort, Acoustomagnetoelasticity, Naukova Dumka, Kiev (1988).

  4. A. I. Lur’e, Nonlinear Theory of Elasticity [in Russian], Nauka, Moscow (1980).

    MATH  Google Scholar 

  5. G. A. Maugin, Continuum Mechanics of Electromagnetic Solids, Elsevier, Amsterdam (1988).

    MATH  Google Scholar 

  6. B. E. Pobedrya, Lectures on Tensor Analysis [in Russian], Moscow University, Moscow (1986).

    MATH  Google Scholar 

  7. C. Truesdell, A First Course in Rational Continuum Mechanics, John Hopkins University, Baltimore, Md. (1972).

    Google Scholar 

  8. S. Helgason, Groups and Geometric Analysis. Integral Geometry, Invariant Differential Operators, and Spherical Functions, Academic, Orlando (1984).

    MATH  Google Scholar 

  9. D. Krupka and J. Janyska, Lectures on Differential Invariants, J. E. Purkyně University, Brno (1990).

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Pidstryhach Institute for Applied Problems of Mechanics and Mathematics, Ukrainian Academy of Sciences, Lviv, Ukraine

    I. B. Prokopovych

Authors
  1. I. B. Prokopovych
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Matematychni Metody ta Fizyko-Mekhanichni Polya, Vol. 51, No. 1, pp. 99–104, January–March, 2008.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Prokopovych, I.B. Differentiation of tensor functions of the state of a body with regard for rotation. J Math Sci 160, 400–406 (2009). https://doi.org/10.1007/s10958-009-9507-y

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-009-9507-y

Keywords

Search

Navigation