Abstract
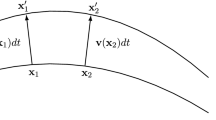
Introducing a concept of twisted tubes, we provide a speculative interpretation of exponent 3/4 in the Vakulenko—Kapitansky estimate for the Faddeev—Skyrme model. This allows us to make an assumption about the domain of applicability of the fit derived from the VK estimate. We propose an example of a sequence of knotted configurations which may be utilized in construction of static solutions with high energies. Bibliography: 9 titles.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
L. D. Faddeev, “Quantization of solitons,” Preprint IAS, print-75-QS70 (1975).
A. J. Niemi, “Dual superconductors and SU(2) Yang—Mills,” JHEP (2004) 035; hep-th/0403175.
E. Babaev, L. D. Faddeev, and A. J. Niemi, Phys. Rev., B65 (2002).
L. D. Faddeev and A. Niemi, “Aspects of electric-magnetic duality in SU(2) Yang—Mills theory,” Phys. Lett., B525, 195–200 (2002).
A. F. Vakulenko and L. V. Kapitansky, Dokl. Akad. Nauk SSSR, 248, 840–842 (1979).
R. S. Ward, “The interaction of two Hopf solitons,” Phys. Lett., B473, 291–296 (2000).
J. Hietarinta and P. Salo, “Ground state in the Faddeev—Skyrme model,” Phys. Rev., D62.
M. Miettinen, A. Niemi, and Yu. Stroganov, “Aspects of duality and confining strings,” Phys. Lett., B474, 303–308 (2000); hep-th/9908178.
R. S. Ward, “Hopf solitons on S 3 and R 3,” DTP-98/55; hep-th/9811176.
Author information
Authors and Affiliations
Additional information
__________
Translated from Zapiski Nauchnykh Seminarov POMI, Vol. 317, 2004, pp. 57–65.
Rights and permissions
About this article
Cite this article
Bolokhov, T.A., Bolokhov, P.A. An interpretation of the Vakulenko—Kapitansky estimate. J Math Sci 136, 3560–3563 (2006). https://doi.org/10.1007/s10958-006-0181-z
Received:
Issue Date:
DOI: https://doi.org/10.1007/s10958-006-0181-z