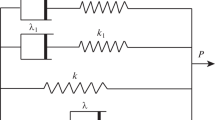
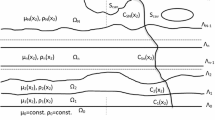
Abstract
The propagation of seismic waves in block two- and three-dimensional media is investigated. These media are composed of identical cells in which there are several fluid blocks and one elastic block. For these media, effective models, which are anisotropic fluids, are established. Formulas for the velocities of propagation in these fluids are derived and investigated. A special investigation is carried out in the cases where the elastic block occupies almost the entire cell or where the relative volume of the elastic block is very small. Bibliography: 9 titles.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
L. A. Molotkov, “Propagation of seismic waves in block elastic-fluid media,” Zap. Nauchn. Semin. POMI, 297, 230–253 (2003).
L. A. Molotkov, “Propagation of seismic waves in block elastic-fluid media,” Zap. Nauchn. Semin. POMI, 297, 254–271 (2003).
L. A. Molotkov, “Propagation of seismic waves in block fluid media,” Zap. Nauchn. Semin. POMI, 308, 124–146 (2004).
M. A. Biot, “Theory of propagation of elastic waves in fluid-saturated porous solid. I. Low-frequency,” J. Acoust. Soc. Amer., 28, No.2, 168–178 (1956).
L. A. Molotkov, “Equivalence of periodically layered and transversely isotropic media,” Zap. Nauchn. Semin. LOMI, 89, 219–233 (1979).
L. A. Molotkov, Investigation of Wave Propagation in Porous and Fractured Media on the Basis of Effective Models of Biot and Layered Media [in Russian], St. Petersburg (2001).
M. W. Lee, O. R. Hutchinson, T. S. Collett, and W. P. Dillon, “Seismic velocities for hydrate-bearing sediments using weighted equation,” J. Geoph. Res., 101, No.B9, 20.347–20.358 (1996).
C. F. Pearson, J. Murphy, and R. Hermes, “Acoustic and resistivity measurments on rock samples containing tetrahydrofuran hydrates,” J. Geoph. Res., 91, 14.132–14.138 (1986).
J. P. Castanga, M. L. Batle, and R. L. Eastwood, “Relationship between compressional-wave and shear-wave velocities in elastic silicate rocks,” Geophysics, 50, 571–581 (1975).
Author information
Authors and Affiliations
Additional information
Dedicated to P. V. Krauklis on the occasion of his seventieth birthday
__________
Translated from Zapiski Nauchnykh Seminarov POMI, Vol. 308, 2004, pp. 147–160.
Rights and permissions
About this article
Cite this article
Molotkov, L.A. Propagation of Seismic Waves in Block Elastic-Fluid Media. III. J Math Sci 132, 83–90 (2006). https://doi.org/10.1007/s10958-005-0477-4
Received:
Issue Date:
DOI: https://doi.org/10.1007/s10958-005-0477-4