Skip to main content
SpringerLink
Log in

Systems of pairs of q-distant representatives, and graph colorings

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

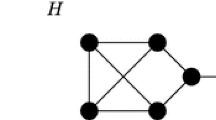
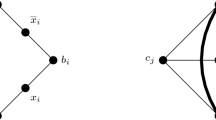
Abstract

The NP-completeness of a number of graph coloring problems related to the frequency assignment problem is proved. For this purpose, we introduce problems concerning systems of pairs of q-distant representatives (which are related to the well-known problem about the system of distinct representatives, but are NP-complete for q ≥ 2), which turned out to be convenient for proving the NP-completeness of various graph coloring problems. Bibliography: 11 titles.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

REFERENCES

  1. M. R. Garey and D. S. Johnson, Computers and Intractability. A Guide to the Theory of NP-Completeness, San Francisco (1979).

  2. R. Battiti, A. A. Bertossi, and M. A. Bonuccelli, “Assigning codes in wireless network:Bounds and scaling properties,” Wireless Networks, 5, No. 3, 195–209 (1999).

    Google Scholar 

  3. H. L. Bodlaender, T. Kloks, R. B. Tan, and J. Leeuwen, “Approximation for λ-coloring of graphs,” Lect. Notes Comput. Sci., 1770, 395–409 (2000).

    Google Scholar 

  4. G. J. Chang and D. Kuo, “The L(2, 1)-labeling problem on graphs,” SIAM J. Discrete Math., 9, 309–316 (1996).

    Google Scholar 

  5. J. Fiala, J. Kratochvil, and A. Proskurowski, “Distance constrained labeling of precoloed trees,” Lect. Notes Comput. Sci., 2202, 285–292 (2001).

    Google Scholar 

  6. J. Fiala, T. Kloks, and J. Kratochvil, “Fixed-parameter complexity of λ-coloring,” Discrete Appl. Math., 113, 59–72 (2001).

    Google Scholar 

  7. D. Fotakis, G. Pantziou, G. Pentaris, and P. Spirakis, “Frequency assignment in mobile and radio networks,” Networks in distributed computing, DIMACS Ser. Discrete Math. Theoret. Comput. Sci., 45 (1997), pp. 73–90.

    Google Scholar 

  8. J. P. Georges and D. W. Mauro, “On the size of graphs labeled with a condition at distance two,” J. Graph Theory, 22, 47–57 (1996).

    Google Scholar 

  9. J. R. Griggs and R. K. Yeh, “Labelling graphs with a condition at distance 2,” SIAM J. Discrete Math., 5, 586–595 (1992).

    Google Scholar 

  10. R. A. Murphey, P. M. Pardalos, and M. G. Resende, “Frequency assignment problems,” AT&T Labs Research Technical Report 98. 16. 1.

  11. D. D.-F. Liu and R. K. Yeh, “On distance two labelling of graphs,” Ars Combin., 47, 13–22 (1997).

    Google Scholar 

Download references

Authors
  1. P. A. Golovach
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Zapiski Nauchnykh Seminarov POMI, Vol. 293, 2002, pp. 5–25.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Golovach, P.A. Systems of pairs of q-distant representatives, and graph colorings. J Math Sci 126, 1141–1151 (2005). https://doi.org/10.1007/s10958-005-0059-5

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-005-0059-5

Keywords

Search

Navigation