Abstract
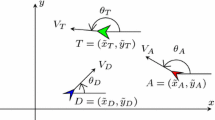
In the Target–Attacker–Defender differential game, an Attacker missile strives to capture a Target aircraft. The Target tries to escape the Attacker and is aided by a Defender missile which aims at intercepting the Attacker, before the latter manages to close in on the Target. The conflict between these intelligent adversaries is naturally modeled as a zero-sum differential game. The Game of Degree when the Attacker is able to win the Target–Attacker–Defender differential game has not been fully solved, and it is addressed in this paper. Previous attempts at designing the players’ strategies have not been proven to be optimal in the differential game sense. In this paper, the optimal strategies of the Game of Degree in the Attacker’s winning region of the state space are synthesized. Also, the value function is obtained, and it is shown that it is continuously differentiable, and it is the solution of the Hamilton–Jacobi–Isaacs equation. The obtained state feedback strategies are compared to recent results addressing this differential game. It is shown that the correct solution of the Target–Attacker–Defender differential game that provides a semipermeable Barrier surface is synthesized and verified in this paper.






Similar content being viewed by others
References
Isaacs, R.: Differential Games. Wiley, New York (1965)
Basar, T., Olsder, G.J.: Dynamic noncooperative game theory, vol. 23. SIAM (1999)
Huang, H., Zhang, W., Ding, J., Stipanovic, D.M., Tomlin, C.J.: Guaranteed decentralized pursuit-evasion in the plane with multiple pursuers. In: 50th IEEE Conference on Decision and Control and European Control Conference, pp. 4835–4840 (2011)
Oyler, D.W., Kabamba, P.T., Girard, A.R.: Pursuit-evasion games in the presence of obstacles. Automatica 65, 1–11 (2016)
Breakwell, J.V., Hagedorn, P.: Point capture of two evaders in succession. J. Optim. Theory Appl. 27(1), 89–97 (1979)
Liu, S.Y., Zhou, Z., Tomlin, C., Hedrick, K.: Evasion as a team against a faster pursuer. In: American Control Conference, pp. 5368–5373 (2013)
Lorenzetti, J., Chen, M., Landry, B., Pavone, M.: Reach-avoid games via mixed-integer second-order cone programming. In: 57th IEEE Conference on Decision and Control, pp. 4409–4416 (2018)
Zhou, Z., Takei, R., Huang, H., Tomlin, C.: A general, open-loop formulation for reach-avoid games. In: 51st IEEE Conference on Decision and Control, pp. 6501–6506 (2012)
Margellos, K., Lygeros, J.: Hamilton–Jacobi formulation for reach-avoid differential games. IEEE Trans. Autom. Control 56(8), 1849–1861 (2011)
Zhou, Z., Ding, J., Huang, H., Takei, R., Tomlin, C.: Efficient path planning algorithms in reach-avoid problems. Automatica 89, 28–36 (2018)
Li, D., Cruz, J.B.: Defending an asset: a linear quadratic game approach. IEEE Trans. Aerosp. Electron. Syst. 47(2), 1026–1044 (2011)
Fisac, J.F., Sastry, S.S.: The pursuit-evasion-defense differential game in dynamic constrained environments. In: IEEE 54th Annual Conference on Decision and Control, pp. 4549–4556 (2015)
Venkatesan, R.H., Sinha, N.K.: A new guidance law for the defense missile of nonmaneuverable aircraft. IEEE Trans. Control Syst. Technol. 23(6), 2424–2431 (2015)
Weintraub, I., Garcia, E., Pachter, M.: A kinematic rejoin method for active defense of non-maneuverable aircraft. In: 2018 American Control Conference, pp. 6533–6538 (2018)
Chen, M., Zhou, Z., Tomlin, C.J.: Multiplayer reach-avoid games via pairwise outcomes. IEEE Trans. Autom. Control 62(3), 1451–1457 (2017)
Zhou, Z., Zhang, W., Ding, J., Huang, H., Stipanović, D.M., Tomlin, C.J.: Cooperative pursuit with Voronoi partitions. Automatica 72, 64–72 (2016)
Pachter, M., Garcia, E., Casbeer, D.W.: Active target defense differential game. In: 52nd Annual Allerton Conference on Communication, Control, and Computing, pp. 46–53 (2014)
Garcia, E., Casbeer, D.W., Pachter, M.: Design and analysis of state-feedback optimal strategies for the differential game of active defense. IEEE Trans. Autom. Control 64(2), 553–568 (2019)
Liang, L., Deng, F., Peng, Z., Li, X., Zha, W.: A differential game for cooperative target defense. Automatica 102, 58–71 (2019)
E. Garcia, D. W. Casbeer, and M. Pachter: Optimal capture strategies in the Target–Attacker–Defender differential game. In: 2018 American Control Conference, pp. 68–73 (2018)
Garcia, E., Casbeer, D.W., Pachter, M.: Pursuit in the presence of a defender. Dyn. Games Appl. 9(3), 652–670 (2019)
Crandall, M.G., Evans, L.C., Lions, P.L.: Some properties of viscosity solutions of Hamilton–Jacobi equations. Trans. Am. Math. Soc. 282(2), 487–502 (1984)
Lions, P.L., Souganidis, P.E.: Differential games, optimal control and directional derivatives of viscosity solutions of Bellman’s and Isaacs’ equations. SIAM J. Control Optim. 23(4), 566–583 (1985)
Getz, W.M., Leitmann, G.: Qualitative differential games with two targets. J. Math. Anal. Appl. 68(2), 421–430 (1979)
Getz, W.M., Pachter, M.: Capturability in a two-target game of two cars. J. Guid. Control Dyn. 4(1), 15–21 (1981)
Ardema, M.D., Heymann, M., Rajan, N.: Combat games. J. Optim. Theory Appl. 46(4), 391–398 (1985)
Pachter, M., Garcia, E., Casbeer, D.W.: Toward a solution of the active target defense differential game. Dyn. Games Appl. 9(1), 165–216 (2019)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Mauro Pontani.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Garcia, E., Casbeer, D.W. & Pachter, M. The Complete Differential Game of Active Target Defense. J Optim Theory Appl 191, 675–699 (2021). https://doi.org/10.1007/s10957-021-01816-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-021-01816-z