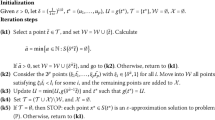Skip to main content
SpringerLink
Log in

Modified Dinkelbach-Type Algorithm for Generalized Fractional Programs with Infinitely Many Ratios

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

In this paper, we extend the Dinkelbach-type algorithm of Crouzeix, Ferland, and Schaible to solve minmax fractional programs with infinitely many ratios. Parallel to the case with finitely many ratios, the task is to solve a sequence of continuous minmax problems,

$$P(\alpha_{k})=\min_{x\in X}\left(\max_{t\in T}\left[f_{t}(x)-\alpha_{k}g_{t}(x) \right]\right)$$

, until {α k } converges to the root of P(α)=0. The solution of P(α k ) is used to generate αk+1. However, calculating the exact optimal solution of P(α k ) requires an extraordinary amount of work. To improve, we apply an entropic regularization method which allows us to solve each problem P(α k ) incompletely, generating an approximate sequence \(\{\tilde{\alpha}_{k}\}\), while retaining the linear convergence rate under mild assumptions. We present also numerical test results on the algorithm which indicate that the new algorithm is robust and promising.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J. P. Crouzeix J. A. Ferland S. Schaible (1983) ArticleTitleDuality in Generalized Linear Fractional Programming Mathematical Programming 27 342–354

    Google Scholar 

  2. J. P. Crouzeix J. A. Ferland S. Schaible (1985) ArticleTitleAn Algorithm for Generalized Fractional Programs Journal of Optimization Theory and Applications 47 35–49 Occurrence Handle10.1007/BF00941314

    Article  Google Scholar 

  3. J. P. Crouzeix J. A. Ferland (1991) ArticleTitleAlgorithms for Generalized Fractional Programming Mathematical Programming 52 191–207 Occurrence Handle10.1007/BF01582887

    Article  Google Scholar 

  4. Schaible, S., Fractional Programming, Handbook of Global Optimization, Edited by R. Horst and P. M. Pardalos, Kluwer Academic Publishers, Dordrecht, Netherlands, pp. 495–608, 1995.

  5. I. M. Stancu-Minasian (1997) Fractional Programming: Theory, Methods, and Applications Kluwer Academic Publishers Dordrecht Netherlands

    Google Scholar 

  6. M. Gugat (1996) ArticleTitleA Fast Algorithm for a Class of Generalized Fractional Programs Management Science 42 1493–1499

    Google Scholar 

  7. A. I. Barros J. B. G. Frenk (1995) ArticleTitleGeneralized Fractional Programming and Cuttting-Plane Algorithms Journal of Optimization Theory and Applications 87 103–120

    Google Scholar 

  8. A. I. Barros J. B. G. Frenk S. Schaible S. Zhang (1996) ArticleTitleA New Algorithm for Generalized Fractional Programs Mathematical Programming 72 147–175 Occurrence Handle10.1016/0025-5610(95)00040-2

    Article  Google Scholar 

  9. J. Gwinner V. Jeyakumar (1993) ArticleTitleA Solvability Theorem and Minimax Fractional Programming Zeitschrift für Operations Research 37 1–12

    Google Scholar 

  10. J. Shi (2001) ArticleTitleA Combined Algorithm for Fractional Programming Annals of Operations Research 103 135–147 Occurrence Handle10.1023/A:1012998904482

    Article  Google Scholar 

  11. L. Abbe (2001) A Logarithmic Barrier Approach and Its Regularization Applied to Convex Semi-Infinite Programming Problems Universität Trier Trier, Germany

    Google Scholar 

  12. S. C. Fang S. Y. Wu (1996) ArticleTitleSolving Min-Max Problems and Linear Semi-Infinite Programs Computers and Mathematics with Applications 32 87–93 Occurrence Handle10.1016/0898-1221(96)00145-9

    Article  Google Scholar 

  13. X. S. Li S. C. Fang (1997) ArticleTitleOn the Entropic Regularization Method for Solving Min-Max Problems with Applications Zeischrift für Operations Research 46 119–130

    Google Scholar 

  14. J. Y. Lin R. L. Sheu (2004) ArticleTitleSolving Continuous Min-Max Problems Using Iteratively Entropic Regularization Method Journal of Optimization Theory and Applications 121 597–612 Occurrence Handle10.1023/B:JOTA.0000037605.19435.63

    Article  Google Scholar 

  15. A. Auslender (1999) ArticleTitlePenalty and Barrier Methods: A Unified Framework SIAM Journal on Optimization 10 211–230 Occurrence Handle10.1137/S1052623497324825

    Article  Google Scholar 

  16. Ben-Tal, A., and Teboulle, M., A Smoothing Technique for Nondifferentiable Optimization Problems, Lecture Notes in Mathematics, Springer-Verlag, Berlin, Germany, Vol. 1405, pp. 1–11, 1989.

  17. Chang P. L., A Minimax Approach to Nonlinear Programming, Doctoral Dissertation, Department of Mathematics, University of Washington, 1980.

  18. J. P. Crouzeix J. A. Ferland S. Schaible (1986) ArticleTitleA Note on an Algorithm for Generalized Fractional Programs Journal of Optimization Theory and Applications 50 183–187 Occurrence Handle10.1007/BF00938484

    Article  Google Scholar 

  19. J. Dieudonné (1969) Foundations of Modern Analysis 10-1 Academic Press New York, NY

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, National Cheng-Kung University, Tainan, Taiwan

    J. Y. Lin & R. L. Sheu

Authors
  1. J. Y. Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. L. Sheu
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

This research was partially supported by the National Science Council of Taiwan under Project NSC 91-2215-M-006-017.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lin, J.Y., Sheu, R.L. Modified Dinkelbach-Type Algorithm for Generalized Fractional Programs with Infinitely Many Ratios. J Optim Theory Appl 126, 323–343 (2005). https://doi.org/10.1007/s10957-005-4717-z

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-005-4717-z

Keywords

Search

Navigation