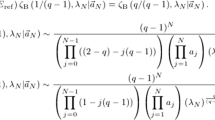Abstract
Usual approach to investigate the statistical properties of deterministically thermostated systems is to analyze the regime of the system motion. In this work the cumulant analysis is used to study the properties of the stationary probability distribution function of the deterministically thermostated harmonic oscillators. This approach shifts attention from the investigation of the geometrical properties of solutions of the systems to the studying a probabilistic measure. The cumulant apparatus is suitable for studying the correlations of dynamical variables, which allows one to reveal the deviation of the actual probabilistic distribution function from canonical one and to evaluate it. Three different thermostats, namely the Nosé–Hoover, Patra-Bhattacharya and Hoover–Holian ones, were investigated. It is shown that their actual distribution functions are non-canonical because of nonlinear coupling of the oscillators with thermostats. The problem of ergodicity of the deterministically thermostated systems is discussed.









Similar content being viewed by others
References
Nose, S.: A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 81, 511–519 (1984)
Hoover, W.G.: Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A 31, 1695–1697 (1985)
Patra, P.K., Bhattacharya, B.: A deterministic thermostat for controlling temperature using all degrees of freedom. J. Chem. Phys. 140, 064106 (2014)
Hoover, W.G., Holian, B.L.: Kinetic moments method for the canonical ensemble distribution. Phys. Lett. A 211, 253–257 (1996)
Kusnezov, D., Bulgac, A., Bauer, W., Kusnezov, D.: Canonical ensembles from Chaos. Ann. Phys. 204, 155–185 (1990)
Martyna, G.J., Klein, M.L., Tuckerman, M.: Nose–Hoover chains: the canonical ensemble via continuous dynamics. J. Chem. Phys. 97, 2635–2643 (1992)
Watanabe, H., Kobayashi, H.: Ergodicity of a thermostat family of the Nose–Hoover type. Phys. Rev. E 75, 040102(R) (2007)
Patra, P.K., Bhattacharya, B.: An ergodic configurational thermostat using selective control of higher order temperatures J. Chem. Phys. 142, 194103-1-8 (2015)
Samoletov, A., Vasiev, V.: Dynamic principle for ensemble control tools. J. Chem. Phys. 147, 204106 (2017)
Posch, H.A., Hoover, W.G., Vesely, F.J.: Canonical dynamics of the Nose oscillator: stability, order, and chaos. Phys. Rev. A 33, 4253–4265 (1986)
Legoll, F., Luskin, M., Moeckel, R.: Non-ergodicity of the Nose–Hoover thermostatted harmonic oscillator. Arch. Ration. Mech. Anal. 184, 449–463 (2007)
Patra, P.K., Bhattacharya, B.: Nonergodicity of the Nose–Hoover chain thermostat in computationally achievable time. Phys. Rev. E 90, 043304 (2014)
Hoover, W.G., Hoover, C.G.: Ergodicity of a time-reversibly thermostated harmonic oscillator and the 2014 Ian Snook Prize. CMST 20, 87–92 (2014)
Hoover, W.G., Hoover, C.G., Isbister, D.J.: Chaos, ergodic convergence, and fractal instability for a thermostated canonical harmonic oscillator. Phys. Rev. E 63, 026209-1-5 (2001)
Patra, P.K., Sprott, J.C., Hoover, W.G., Hoover, C.G.: Deterministic time-reversible thermostats: chaos, ergodicity, and the zeroth law of thermodynamics. Mol. Phys. 113, 2863–2872 (2015)
Hoover, W.G., Hoover, C.G.: Ergodicity of the Martyna–Klein–Tuckerman thermostat and the 2014 Ian Snook Prize. CMST 21, 5–10 (2015)
Hoover, W.G., Sprott, J.C., Patra, P.K.: Ergodic time-reversible chaos for Gibbs canonical oscillator. Phys. Lett. A 379, 2935–2940 (2015)
Samoletov, A.A., Dettman, C.P., Chaplain, C.P.: Thermostats for slow configurational modes. J. Stat. Phys. 128, 1321–1336 (2007)
Malakhov, A.N.: Cumulant Analysis of Random Non-Gaussian Processes and their Transformation. Sovetskoe Radio, Moscow (1978). (in Russian)
Primak, S., Kontorovich, V., Lyandres, V.: Stochastic Methods and their Applications to Communications. Stochastic Differential Equations Approach. Wiley, New York (2004)
Kontorovich, V.: Applied statistical analysis for strange attractors and related problems. Math. Methods Appl. Sci. 30, 1705–1717 (2007)
Hockney, R.W.: The potential calculation and some applications. Methods Comput. Phys. 9, 136–211 (1970)
Verlet, L.: Computer “experiment” on classical fluids. 1. Thermodynamical properties of Lennard-Jones molecules. Phys. Rev. 159, 98–103 (1967)
Lichtenberg, A.J., Liberman, M.A.: Regular and Stochastic Motion. Springer, New York (1983)
Eckmann, J.-P., Ruelle, D.: Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 57 (1985)
Thompson, J.M.T., Stewar, H.B.: Nonlinear Dynamics and Chaos. Wiley, New York (1986)
Acknowledgements
The author thanks A. Samoletov for interesting and useful discussions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A The Expressions that are Referenced in the Text
A The Expressions that are Referenced in the Text
The opening of the cumulant brackets used in the text.
The example of the cumulants expressed in terms of the moments
Rights and permissions
About this article
Cite this article
Artemov, A.N. Cumulant Analysis of the Statistical Properties of a Deterministically Thermostated Harmonic Oscillator. J Stat Phys 174, 992–1010 (2019). https://doi.org/10.1007/s10955-019-02220-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-019-02220-8