Abstract
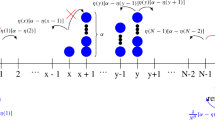
We consider an interacting particle system in the interval [1, N] with reservoirs at the boundaries. While the dynamics in the channel is the simple symmetric exclusion process, the reservoirs are also particle systems which interact with the given system by exchanging particles. In this paper we study the case where the size of each reservoir is the same as the size of the channel. We will prove that the hydrodynamic limit equation is the heat equation with boundary conditions which relate first and second spatial derivatives at the boundaries for which we will prove the existence and uniqueness of weak solutions.

Similar content being viewed by others
References
Amir, M.: Sticky Brownian motion as the strong limit of a sequence of random walks. Stoch. Process. Their Appl. 39(2), 221–237 (1991)
Cannon, J.R.: The One-Dimensional Heat Equation. Addison-Wesley Publishing Company, Menlo Park (1984)
De Masi, A., Olla, S.: Quasi-static hydrodynamic limits. J. Stat. Phys. 161(5), 10371058 (2015)
De Masi, A., Presutti, E., Tsagkarogiannis, D., Vares, M.E.: Current reservoirs in the simple exclusion process. J. Stat. Phys. 144(6), 1151–1170 (2011)
De Masi, A., Presutti, E., Tsagkarogiannis, D., Vares, M.E.: Truncated correlations in the stirring process with births and deaths. Electron. J. Probab. 17, 1–35 (2012)
De Masi, A., Presutti, E., Tsagkarogiannis, D., Vares, M.E.: Extinction time for a random walk in a random environment. Bernoulli 21(3), 1824–1843 (2015). https://doi.org/10.3150/14-BEJ627
De Masi, A., Presutti, E., Tsagkarogiannis, D., Vares, M.E.: Exponential rate of convergence in current reservoirs. Bernoulli 21(3), 1844–1854 (2015). https://doi.org/10.3150/14-BEJ628
Galves, A., Kipnis, C., Marchioro, C., Presutti, E.: Non equilibrium measures which exhibit a temperature gradient: study of a model. Commun. Math. Phys. 81, 124–147 (1981)
Knight, F.B.: On the random walk and Brownian motion. Trans. Am. Math. Sot. 103, 725–731 (1961)
Liggett, T.M.: Interacting Particle Systems. Springer, New York (1985)
Lawler, G., Limic, V.: Random Walk: A Modern Introduction. Cambridge Studies in Advanced Mathematics, vol. 123. Cambridge University Press, Cambridge (2010)
Miller, R.K., Feldstein, A.: Smoothness of solutions of Volterra integral equations with weakly singular kernels. SIAM J. Math. Anal. 2, 242–258 (1971)
Peskir, G.: A probabilistic solution to the Stroock-Williams equation. Ann. Probab. 42(5), 2197–2206 (2014). https://doi.org/10.1214/13-AOP865
Stroock, D.W., Williams, D.: A simple PDE and Wiener–Hopf Riccati equations. Commun. Pure Appl. Math. 58, 11161148 (2005)
Acknowledgements
I greatly appreciate Prof. Errico Presutti for suggesting the problem and offering me a large number of useful ideas. I also would like to express my gratitude to Lorenzo Bertini, Paolo Butta, Anna De Masi, Pablo Ferrari and Frank Redig and Maria Eulalia Vares for their valuable comments and suggestions. In addition, I would like to thank the reviewers for their careful reading of my paper and for their insightful comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Nguyen, T.D.T. Fick Law and Sticky Brownian Motions. J Stat Phys 174, 494–518 (2019). https://doi.org/10.1007/s10955-018-2190-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-018-2190-y