Adaptive Importance Sampling for Control and Inference

Abstract

Path integral (PI) control problems are a restricted class of non-linear control problems that can be solved formally as a Feynman–Kac PI and can be estimated using Monte Carlo sampling. In this contribution we review PI control theory in the finite horizon case. We subsequently focus on the problem how to compute and represent control solutions. We review the most commonly used methods in robotics and control. Within the PI theory, the question of how to compute becomes the question of importance sampling. Efficient importance samplers are state feedback controllers and the use of these requires an efficient representation. Learning and representing effective state-feedback controllers for non-linear stochastic control problems is a very challenging, and largely unsolved, problem. We show how to learn and represent such controllers using ideas from the cross entropy method. We derive a gradient descent method that allows to learn feed-back controllers using an arbitrary parametrisation. We refer to this method as the path integral cross entropy method or PICE. We illustrate this method for some simple examples. The PI control methods can be used to estimate the posterior distribution in latent state models. In neuroscience these problems arise when estimating connectivity from neural recording data using EM. We demonstrate the PI control method as an accurate alternative to particle filtering.

1 Introduction

Stochastic optimal control theory (SOC) considers the problem to compute an optimal sequence of actions to attain a future goal. The optimal control is usually computed from the Bellman equation, which is a partial differential equation. Solving the equation for high dimensional systems is difficult in general, except for special cases, most notably the case of linear dynamics and quadratic control cost or the noiseless deterministic case. Therefore, despite its elegance and generality, SOC has not been used much in practice.

In [13] it was observed that posterior inference in a certain class of diffusion processes can be mapped onto a stochastic optimal control problem. These so-called path integral (PI) control problems [20] represent a restricted class of non-linear control problems with arbitrary dynamics and state cost, but with a linear dependence of the control on the dynamics and quadratic control cost. For this class of control problems, the Bellman equation can be transformed into a linear partial differential equation. The solution for both the optimal control and the optimal cost-to-go can be expressed in closed form as a Feynman–Kac path integral. The path integral involves an expectation value with respect to a dynamical system. As a result, the optimal control can be estimated using Monte Carlo sampling. See [21, 22, 45, 47] for earlier reviews and references.

In this contribution we review path integral control theory in the finite horizon case. Important questions are: how to compute and represent the optimal control solution. In order to efficiently compute, or approximate, the optimal control solution we discuss the notion of importance sampling and the relation to the Girsanov change of measure theory. As a result, the path integrals can be estimated using (suboptimal) controls. Different importance samplers all yield the same asymptotic result, but differ in their efficiency. We show an intimate relation between optimal importance sampling and optimal control: we prove a Lemma that shows that the optimal control solution is the optimal sampler, and better samplers (in terms of effective sample size) are better controllers (in terms of control cost) [46]. This allows us to iteratively improve the importance sampling, thus increasing the efficiency of the sampling.

In addition to the computational problem, another key problem is the fact that the optimal control solution is in general a state- and time-dependent function u(x, t) with u the control, x the state and t the time. The state dependence is referred to as a feed-back controller, which means that the execution of the control at time t requires knowledge of the current state x of the system. It is often impossible to compute the optimal control for all states because this function is an infinite dimensional object, which we call the representation problem. Within the robotics and control community, there are several approaches to deal with this problem.

1.1 Deterministic Control and Local Linearisation

The simplest approach follows from the realisation that state-dependent control is only required due to the noise in the problem. In the deterministic case, one can compute the optimal control solution $u(t)=u^*(x^*(t),t)$ along the optimal path $x^*(t)$ only, and this is a function that only depends on time. This is a so-called open loop controller which applies the control u(t) regardless of the actual state that the system is at time t. This approach works for certain robotics tasks such a grasping or reaching. See for instance [36, 44] who constructed open loop controllers for a number of robotics tasks within the path integral control framework. Such state-independent control solutions can yield stable solutions with variable stiffness and feedback gains, when the dynamics itself has the proper state dependence (for instance by using dynamic motor primitives). However, open loop controllers are clearly sub-optimal in general and simply fail for unstable dynamical systems that require state feedback.

It should be mentioned that the open loop approach can be stabilised by computing a linear feed-back controller around the deterministic trajectory. This approach uses the fact that for linear dynamical systems with Gaussian noise and with quadratic control cost, the solution can be efficiently computed.¹ One defines a linear quadratic control problem around the deterministic optimal trajectory $x^*(t)$ by Taylor expansion to second order, which can be solved efficiently. The result is a linear feedback controller that stabilises the trajectory $x^*(t)$. This two-step approach is well-known and powerful and at the basis of many control solutions such as the control of ballistic missiles or chemical plants [37].

The solution of the linear quadratic control problem also provides a correction to the optimal trajectory $x^*(t)$. Thus, a new $x^*(t)$ is obtained and a new LGQ problem can be defined and solved. This approach can be iterated, incrementally improving the trajectory $x^*(t$) and the linear feedback controller. This approach is known as differential dynamic programming [26, 30] or the iterative LQG method [48].

1.2 Model Predictive Control

A second idea is to compute the control ‘at run-time’ for any state that is visited using the idea of model predictive control (MPC) [7]. At each time t in state $x_t$, one defines a finite horizon control problem on the interval $[t,t+T]$ and computes the optimal control solution $u(s,x_s), t\le s\le t+T$ on the entire interval. One executes the dynamics using $u(t,x_t)$ and the system moves to a new state $x_{t+dt}$ as a result of this control and possible external disturbances. This approach is repeated for each time. The method relies on a model of the plant and external disturbances, and on the possibility to compute the control solution sufficiently fast. MPC yields a state dependent controller because the control solution in the future time interval depends on the current state. MPC avoids the representation problem altogether, because the control is never explicitly represented for all states, but computed for any state when needed.

In the robotics community, the combination of DDP with MPC is a popular approach, providing a practical compromise between stability, non-linearity and efficient computation and has been succesfully applied to robot walking and manipulation [29, 43] and aerobatic helicopter flight [1].

MPC is particularly well-suited for the path integral control problems, because in this case the optimal control $u^*(x,t)$ is explicitly given in terms of a path integral. The challenge then is to evaluate this path integral sufficiently accurate in real time. Thijssen and Kappen [46] propose adaptive Monte Carlo sampling that is accelerated using importance sampling. This approach has been successfully applied to the control of 10–20 autonomous helicopters (quadrotors) that are engaged in coordinated control tasks such as flying with minimal velocity in a restricted area without collision or a task where multiple ’cats’ need to catch a mouse that tries to get away [18].

1.3 Reinforcement Learning

Reinforcement learning (RL) is a particular setting of control problems with the emphasis on learning a controller on the basis of trial-and-error. A sequence of states $X_t, t=0,dt,2dt,\ldots ,$ is generated from a single roll-out of the dynamical system using a particular control, which is called the policy in RL. The ‘learning’ in reinforcement learning refers to the estimation of a parametrised policy $u(t,x||\theta )$, called function approximation, from a single roll out [39]. The use of function approximation in RL is not straightforward [4, 5, 38]. To illustrate the problem, consider the infinite horizon discounted reward case, which is the most popular RL setting. The problem is to compute the optimal cost-to-go of a particular parametrised form: $J(x|\theta )$. In the non-parametrised case, the solution is given by the Bellman ‘back-up’ equation, which relates $J(x_t)$ to $J(x_{t+dt})$ where $x_{t,t+dt}$ are the states of the system at time $t,t+dt$, respectively and $x_{t+dt}$ is related to $x_t$ through the dynamics of the system. In the parametrised case, one must compute the new parameters $\theta '$ of $J(x_t|\theta ')$ from $J(x_{t+dt}|\theta )$ . The problem is that the update is in general not of the parametrised form and an additional approximation is required to find the $\theta '$ that gives the best approximation. In the RL literature, one makes the distinction between ’on-policy’ learning where J is only updated for the sequence of states that are visited, and off-policy learning updates J(x) for all states x, or a (weighted) set of states. Convergence of RL with function approximation has been shown for on-policy learning with linear function approximation (i.e. J is a linear function of $\theta$) [49]. These authors also provide examples of both off-policy learning and non-linear function approximation where learning does not converge.

1.4 Outline

This chapter is organised as follows. In Sect. 2 we present a review of the main ingredients of the path integral control method. We define the path integral control problem and state the basic Theorem of its solution in terms of a path integral. We then prove the Theorem by showing in Sect. 2.1 that the Bellman equation can be linearised by a log transform and in Sect. 2.2 that the solution of this equation is given in terms of a Feynman–Kac path integral. In Sect. 2.3 we discuss how to efficiently estimate the path integral using the idea of importance sampling. We show that the optimal importance sampler coincides with the optimal control.

Thus, a good control solution can be used to accelerate the computation of a better control solution. Such a solution is a state-feedback controller, i.e.. a function of t, x for a larger range of t, x values. This leads to the issue how to compute and represent such a solution. The path integral Theorem shows how to compute the solution u(t, x) for a given t, x, but repeating this computation for all t, x is clearly infeasible.

A solution to this problem was first proposed in [50] to use the cross entropy method to improve importance sampling for diffusion processes. Their approach follows quite closely the original cross entropy method by De Boer et al. [9]. In particular, they restrict themselves to a control function that is linearly parametrised so that the optimisation is a convex problem. In our work, we generalise this idea to arbitrary parametrisation, resulting in a gradient based method. In Sect. 3 we review the cross entropy method, as an adaptive procedure to compute an optimised importance sampler in a parametrised family of distributions over trajectories. In order to apply the cross entropy method in our context, we reformulate the path integral control problem in terms of a KL divergence minimisation in Sect. 3.1 and in Sect. 3.2 we apply this procedure to obtain optimal samplers/controllers to estimate the path integrals. We refer to this method as the path integral cross entropy (PICE) method. In Sect. 4 we illustrate the PICE method to learn a time-independent state-dependent controller for some simple control tasks involving a linear and a non-linear parametrisation.

In Sect. 5 we consider the reverse connection between control and sampling: we consider the problem to compute the posterior distribution of a latent state model that we wish to approximate using Monte Carlo sampling, and to use optimal controls to accelerate this sampling problem. In neuroscience, such problems arise, e.g. to estimate network connectivity from data or decoding of neural recordings. The common approach is to formulate a maximum likelihood problem that is optimised using the EM method. The E-step is a Bayesian inference problem over hidden states and is shown to be equivalent to a path integral control problem. We illustrate this for a small toy neural network where we estimate the neural activity from noisy observations.

2 Path Integral Control

Consider the dynamical system

$$\begin{aligned}&dX(s)=f(s,X(s))ds+g(s,X(s))\Big (u(s,X(s))ds+ dW(s)\Big )\qquad t\le s\le T \end{aligned}$$

(1)

with $X(t)=x$. dW(s) is Gaussian noise with ${\mathbb {E}}\ dW(s)=0, {\mathbb {E}}\ dW(s)dW(r) =ds\delta (s-r)$. The stochastic process $W(s), t\le s\le T$ is called a Brownian motion. We will use upper case for stochastic variables and lower case for deterministic variables. t denotes the current time and T the future horizon time.

Given a function u(s, x) that defines the control for each state x and each time $t\le s\le T$, define the cost

$$\begin{aligned} S(t,x,u)&=\Phi (X(T))+\int _t^T\left( V(s,X(s))+\frac{1}{2} u(s,X(s))^2\right) ds \nonumber \\&\quad +\int _t^T u(s,X(s)) dW(s) \end{aligned}$$

(2)

with t, x the current time and state and u the control function. The stochastic optimal control problem is to find the optimal control function u:

$$\begin{aligned} J(t,x)&=\min _{u}{\mathbb {E}}_u \ S(t,x,u)\nonumber \\ u^*(t,x)&=\arg \min _{u}{\mathbb {E}}_u \ S(t,x,u) \end{aligned}$$

(3)

where ${\mathbb {E}}_u$ is an expectation value with respect to the stochastic process Eq. 1 with initial condition $X_t=x$ and control u.

J(t, x) is called the optimal cost-to-go as it specifies the optimal cost from any intermediate state and any intermediate time until the end time $t=T$. For any control problem, J satisfies a partial differential equation known as the Hamilton–Jacobi–Bellman equation (HJB). In the special case of the path integral control problems the solution is given explicitly as follows.

Theorem 1

The solution of the control problem Eq. 3 is given by

$$\begin{aligned} J(t,x)= & {} -\log \psi (t,x) \qquad \psi (t,x)= {\mathbb {E}}_u\ e^{-S(t,x,u)}\end{aligned}$$

(4)

$$\begin{aligned} u^*(t,x)= & {} u(t,x) +\left< \frac{dW(t)}{dt} \right> \end{aligned}$$

(5)

where we define

$$\begin{aligned} \left< \frac{dW}{dt} \right>&=\lim _{s\downarrow t} \frac{1}{s-t} \frac{{\mathbb {E}}_u\left[ W(s) e^{-S(t, x,u)}\right] }{{\mathbb {E}}_u \left[ e^{-S(t, x,u)}\right] } \end{aligned}$$

(6)

and $W(s), s\ge t$ the Brownian motion.

The path integral control problem and Theorem 1 can be generalised to the multi-dimensional case where X(t), f(s, X(s)) are n-dimensional vectors, u(s, X(s)) is an m dimensional vector and g(s, X(s)) is an $n\times m$ matrix. dW(s) is m-dimensional Gaussian noise with ${\mathbb {E}}_u\ dW(s)=0$ and ${\mathbb {E}}_u \ dW(s)dW(r) =\nu ds\delta (s-r)$ and $\nu$ the $m\times m$ positive definite covariance matrix. Eqs. 1 and 2 become:

$$\begin{aligned} dX(s)= & {} f(s,X(s))ds+g(s,X(s))\Big (u(s,X(s))ds+ dW(s)\Big )\quad t\le s\le T\nonumber \\ S(t,x,u)= & {} \frac{1}{\lambda }\left( \Phi (X(T))+\int _t^T\left( V(s,X(s))+\frac{1}{2} u(s,X(s))' R u(s,X(s))\right) ds \right. \nonumber \\&\left. +\int _t^T u(s,X(s))' R dW(s)\right) \end{aligned}$$

(7)

where $'$ denotes transpose. In this case, $\nu$ and R must be related as with $\lambda I = R \nu$ with $\lambda >0$ a scalar [20].

In order to understand Theorem 1, we first will derive in Sect. 2.1 the HJB equation and show that for the path integral control problem it can be transformed into a linear partial differential equation. Subsequently, in Sect. 2.2 we present a Lemma that will allow us prove the Theorem.

2.1 The Linear HJB Equation

The derivation of the HJB equation relies on the argument of dynamic programming. This is quite general, but here we restrict ourselves to the path integral case. Dynamic programming expresses the control problem on the time interval [t, T] as an instantaneous contribution at the small time interval $[t,t+ds]$ and a control problem on the interval $[t+ds,T]$. From the definition of J we obtain that $J(T,x)=\Phi (x), \forall x$.

We derive the HJB equation by discretising time with infinitesimal time increments ds. The dynamics and cost-to-go become

$$\begin{aligned} X_{s+ds}= & {} X_s +f_s(X_s)ds+g_s(X_s)\Big (u_s(X_s)ds+ dW_s\Big ) \quad s=t,t+ds,\ldots ,T-ds\\ S_t(X,u_{t:T-ds})= & {} \Phi (X_T)+\sum _{s=t}^{T-ds}ds \left( V_s(X_s)+\frac{1}{2} u_s(X_s)^2\right) +\sum _{s=t}^{T-ds} u_s(X_s) dW_s \end{aligned}$$

The minimisation in Eq. 3 is with respect to a function u of state and time and becomes a minimisation over a sequence of state-dependent functions $u_{t:T-ds}=\{u_s(x_s), s=t,t+ds,\ldots , t+T-ds\}$:

$$\begin{aligned} J_t(x_t)= & {} \min _{u_{t:T-ds}}{\mathbb {E}}_u \ S_t(x_t,u_{t:T-ds})\\= & {} \min _{u_{t}} \left( V_t(x_t)ds+\frac{1}{2} u_t(x_t)^2 ds+\min _{u_{t+ds:T-ds}} {\mathbb {E}}_u \ S_{t+ds}(X_{t+ds}, u_{t+ds:T-ds})\right) \\= & {} \min _{u_t} \left( V_t(x_t)ds+\frac{1}{2} u_t(x_t)^2ds+{\mathbb {E}}_u \ J_{t+ds}(X_{t+ds})\right) \\= & {} \min _{u_t} \left( V_t(x_t)ds+\frac{1}{2} u_t(x_t)^2 ds+J_t(x_t) +ds( f_t(x_t)+g_t(x_t) u_t(x_t))\partial _x J_t(x_t)\right. \\&+\left. \frac{1}{2}ds \partial ^2_x J_t(x_t)+\partial _t J_t(x_t)ds +{\mathcal {O}}(ds^2)\right) \end{aligned}$$

The first step is the definition of $J_t$. The second step separates the cost term at time t from the rest of the contributions in $S_t$, uses that ${\mathbb {E}}dW_t=0$. The third step identifies the second term as the optimal cost-to-go from time $t+ds$ in state $X_{t+ds}$. The expectation is with respect to the next future state $X_{t+ds}$ only. The fourth step uses the dynamics of x to express $X_{t+ds}$ in terms of $x_t$, a first order Taylor expansion in ds and a second order Taylor expansion in $X_{t+ds}-x_t$ and uses the fact that ${\mathbb {E}}X_{t+ds}-x_t =(f_t(x_t) + g_t(x_t)u_t(x_t))ds$ and ${\mathbb {E}}(X_{t+ds}-x_t)^2 = {\mathbb {E}}dW_t^2 +{\mathcal {O}}(ds^2)=ds +{\mathcal {O}}(ds^2)$. $\partial _{t,x}$ are partial derivatives with respect to t, x respectively.

Note, that the minimisation of control paths $u_{t:T-ds}$ is absent in the final result, and only a minimisation over $u_t$ remains. We obtain in the limit $ds\rightarrow 0$:

$$\begin{aligned} -\partial _t J(t,x)= & {} \min _u\left( V(t,x)+\frac{1}{2}u^2(t,x) + (f(t,x)+g(t,x)u(t,x))\partial _x J(x,t)\right. \nonumber \\&+\left. \frac{1}{2}g(t,x)^2 \partial _x^2 J(t,x)\right) \end{aligned}$$

(8)

Equation 8 is a partial differential equation, known as the HJB equation, that describes the evolution of J as a function of x and t and must be solved with boundary condition $J(x,T)=\phi (x)$.

Since u appears linear and quadratic in Eq. 8, we can solve the minimisation with respect to u which gives $u^*(t,x)=- g(t,x) \partial _x J(t,x)$. Define $\psi (t,x)=e^{-J(t,x)}$, then the HJB equation becomes linear in $\psi$:

$$\begin{aligned} \partial _t \psi + f \partial _x \psi + \frac{1}{2} g^2 \partial _x^2 \psi = V\psi . \end{aligned}$$

(9)

with boundary condition $\psi (T,x)=e^{-\Phi (x)}$.

2.2 Proof of the Theorem

In this section we show that Eq. 9 has a solution in terms of a path integral (see [46]). In order to prove this, we first derive the following Lemma. The derivation makes use of the so-called Itô calculus which we have summarised in the appendix.

Lemma 1

Define the stochastic processes $Y(s),Z(s), t\le s\le T$ as functions of the stochastic process Eq. 1:

$$\begin{aligned} Z(s)= & {} \exp (-Y(s)))\quad Y(s)\nonumber \\= & {} \int _t^s V(r,X_r)dr + \frac{1}{2} u(r,X_r)^2dr+u(r,X_r) dW(r)\quad t\le s\le T \end{aligned}$$

(10)

When $\psi$ is a solution of the linear Bellman equation Eq. 9 and $u^*$ is the optimal control, then

$$\begin{aligned} e^{-S(t,x,u)} - \psi (t,x)&= \int _{t}^{T} Z(s)\psi (s,X_s) (u^*(s,X_s)-u(s,X_s)) dW(s) \end{aligned}$$

(11)

Proof

Consider $\psi (s,X(s)), t\le s\le T$ as a function of the stochastic process Eq. 1. Since X(s) evolves according to Eq. 1, $\psi$ is also a stochastic process and we can use Itô’s Lemma (Eq. 32) to derive a dynamics for $\psi$.

$$\begin{aligned}&d\psi =\left( \partial _t \psi + (f+gu) \partial _x \psi + \frac{1}{2} \ g^2 \partial _x^2 \psi \right) ds +g dW \partial _x \psi =V\psi ds + g(uds+dW)\partial _x \psi \end{aligned}$$

where the last equation follows because $\psi$ satisfies the linear Bellman equation Eq. 9.

From the definition of Y we obtain $dY=Vds + \frac{1}{2}u^2 ds + u dW$. Using again Itô’s Lemma Eq. 32:

$$\begin{aligned} dZ =-Z dY + \frac{1}{2}Z d[Y,Y]= -Z\left( V ds +udW\right) \end{aligned}$$

Using the product rule Eq. 31 we get

$$\begin{aligned} d(Z\psi )=\psi dZ+Z d\psi +d[Z,\psi ]= -Z\psi u dW+Z\partial _x \psi g dW=Z\psi (u^*-u)dW \end{aligned}$$

where in the last step we used that $u^*=\frac{1}{\psi } g \partial _x \psi$ which follows from $u^*(t,x)=- g(t,x) \partial _x J(t,x)$. and $\psi (t,x)=e^{-J(t,x)}$ (see Sect. 2.1). Integrating $d(Z\psi )$ from t to T using Eq. 33 yields

$$\begin{aligned} Z(T)\psi (T)-Z(t)\psi (t,x)= & {} \int _t^T d(Z\psi )\\ e^{-Y(T)-\Phi (X(T))}-\psi (t,x)= & {} \int _t^T ds Z\psi (u^*-u)dW \end{aligned}$$

where we used that $Z(t)=1$ and $\psi (T)=\exp (-\Phi (X(T)))$. This proves Eq. 11. $\square$

With the Lemma, it is easy to prove Theorem 1. Taking the expected value in Eq. 11 proves Eq. 4

$$\begin{aligned} \psi (t,x) = {\mathbb {E}}_u\left[ e^{-S(t, x,u)}\right] \end{aligned}$$

This is a closed form expression for the optimal cost-to-go as a path integral.

To prove Eq. 5, we multiply Eq. 11 with $W(s)=\int _{t}^{s}dW$, which is an increment of the Wiener process and take the expectation value:

$$\begin{aligned} {\mathbb {E}}_u\left[ e^{-S(t,x,u)} W(s) \right] ={\mathbb {E}}_u\left[ \int _t^sZ\psi (u^*-u) dW \int _t^sdW \right] =\int _t^s{\mathbb {E}}_u\left[ Z\psi (u^*-u) \right] dr \end{aligned}$$

where in the first step we used ${\mathbb {E}}_u W(s)=0$ and in the last step we used Itô Isometry Eq. 35. To get $u^*$ we divide by the time increment $s-t$ and take the limit of the time increment to zero. This will yield the integrand of the RHS $\psi (t,x)(u^*(t,x)-u(t,x)$. Therefore the expected value disappears and we get

$$\begin{aligned} u^*(t,x)=u(t,x)+\frac{1}{\psi (t,x)} \lim _{s\downarrow t}\frac{1}{s-t} {\mathbb {E}}_u\left[ e^{-S(t,x,u)} W(s) \right] \end{aligned}$$

which is Eq. 5.

2.3 Monte Carlo Sampling

Theorem 1 gives an explicit expression for the optimal control $u^*(t,x)$ and the optimal cost-to-go J(t, x) in terms of an expectation value over trajectories that start at x at time t until the horizon time T. One can estimate the expectation value by Monte Carlo sampling. One generates N trajectories $X(t)_i, i=1,\ldots , N$ starting at x, t that evolve according to the dynamics Eq. 1. Then, $\psi (t,x)$ and $u^*(t,x)$ are estimated as

$$\begin{aligned} \hat{\psi }(t,x)= & {} \sum _{i=1}^N w_i \qquad w_i= \frac{1}{N} e^{-S_i(t,x,u)} \end{aligned}$$

(12)

$$\begin{aligned} \hat{u}^*(t,x)= & {} u(t,x)+\frac{1}{\hat{\psi }(t,x)}\lim _{s\downarrow t} \frac{1}{s-t}\sum _{i=1}^N W(s)_i w_i \end{aligned}$$

(13)

with $S_i(t,x,u)$ the value of S(t, x, u) from Eq. 2 for the ith trajectory $X(s)_i, W(s)_i, t\le s\le T$. The optimal control estimate involves a limit which we must handle numerically by setting $s-t=\epsilon >0$. Although in theory the result holds in the limit $\epsilon \rightarrow 0$, in practice $\epsilon$ should be taken a finite value because of numerical instability, at the expense of theoretical correctness.

The estimate involves a control u, which we refer to as the sampling control. Theorem 1 shows that one can use any sampling control to compute these expectation values. The choice of u affects the efficiency of the sampling. The efficiency of the sampler depends on the variance of the weights $w_i$ which can be easily understood. If the weight of one sample dominates all other weights, the weighted sum over N terms is effectively only one term. The optimal weight distributions for sampling is obtained when all samples contribute equally, which means that all weights are equal. It can be easily seen from Lemma 1 that this is obtained when $u=u^*$. In that case, the right hand side of Eq. 11 is zero and thus is $S(t,x,u^*)$ a deterministic quantity. This means that for all trajectories $X_i(t)$ the value $S_i(t,x,u^*)$ is the same (and equal to the optimal cost-to-go J(t, x)). Thus, sampling with $u^*$ has zero variance meaning that all samples yield the same result and therefore only one sample is required. One can also deduce from Lemma 1 that when u is close to $u^*$, the variance in the right hand side of Eq. 11 as a result of the different trajectories is small and thus is the variance in $w_i=e^{-S_i(t,x,u)}$ is small. Thus, the closer u is to $u^*$ the more effective is the importance sampler [46].

One can thus view the choice of u as implementing a type of importance sampling and the optimal control $u^*$ is the optimal importance sampler. The relation between control and importance sampling can also be understood through the Girsanov change of measure [16]. The change of measure introduces a drift term in the dynamics (which is the control term) that can be chosen such that it reduces the variance of the estimate. The optimal change of measure has zero variance and is achieved by a state dependent drift [23, 27].

Despite these elegant theoretical results, this idea has not been used much in practice. The essential problem is the representation of the controller as a parametrised model and how to adapt the parameters such as to optimise the importance sampler. Newton [32] constructs (non-adaptive) importance samplers based on projective approximation onto stochastic processes. Dupuis and Wang [11] expresses optimal importance sampling using large deviations as a differential game. This yields a game theoretic Bellman equation which in practice is difficult to solve. In [50] a first generic adaptive approach was introduced based on the cross entropy method for controllers that depend linear on the parameters. Here, we extend their idea to arbitrary parametrised models.

3 The Cross-Entropy Method

The cross-entropy method [9] is an adaptive approach to importance sampling. Let X be a random variable taking values in the space ${\mathcal {X}}$. Let $f_v(x)$ be a family of probability density function on ${\mathcal {X}}$ parametrised by v and h(x) be a positive function. Suppose that we are interested in the expectation value

$$\begin{aligned} l={\mathbb {E}}_u \ h =\int dx f_u(x) h(x) \end{aligned}$$

(14)

where ${\mathbb {E}}_u$ denotes expectation with respect to the pdf $f_u$ for a particular value of $v=u$. A crude estimate of l is by naive Monte Carlo sampling from $f_u$: Draw N samples $X_i,i=1,\ldots , N$ from $f_u$ and construct the estimator

$$\begin{aligned} \hat{l}=\frac{1}{N}\sum _{i=1}^N h(X_i) \end{aligned}$$

(15)

The estimator is a stochastic variable and is unbiased, which means that its expectation value is the quantity of interest: ${\mathbb {E}}_u \hat{l}=l$. The variance of $\hat{l}$ quantifies the accuracy of the sampler. The accuracy is high when many samples give a significant contribution to the sum. However, when the supports of $f_u$ and h have only a small overlap, most samples $X_i$ from $f_u$ will have $h(X_i)\approx 0$ and only few samples effectively contribute to the sum. In this case the estimator has high variance and is inaccurate.

A better estimate is obtained by importance sampling. The idea is to define an importance sampling distribution g(x) and to sample N samples from g(x) and construct the estimator:

$$\begin{aligned} \hat{l}=\frac{1}{N}\sum _{i=1}^N h(X_i) \frac{f_u(X_i)}{g(X_i)} \end{aligned}$$

(16)

It is easy to see that this estimator is also unbiased: ${\mathbb {E}}_g \hat{l} = \frac{1}{N}\sum _i {\mathbb {E}}_g h(X)\frac{f_u(X)}{g(X)}={\mathbb {E}}_u h(X) = l$. The question now is to find a g such that $\hat{l}$ has low variance. When $g=f_u$ Eq. 16 reduces to Eq. 15.

Before we address this question, note that it is easy to construct the optimal importance sampler. It is given by

$$\begin{aligned} g^*(x)=\frac{h(x) f_u(x)}{l} \end{aligned}$$

where the denominator follows from normalisation: $1=\int dx g^*(x)$. In this case the estimator Eq. 16 becomes $\hat{l}=l$ for any set of samples. Thus, the optimal importance sampler has zero variance and l can be estimated with one sample only. Clearly $g^*$ cannot be used in practice since it requires l, which is the quantity that we want to compute!

However, we may find an importance sampler that is close to $g^*$. The cross entropy method suggests to find the distribution $f_v$ in the parametrised family of distributions that minimises the KL divergence

$$\begin{aligned} KL(g^*|f_v)=\int dx g^*(x) \log \frac{g^*(x)}{f_v(x)}\propto -{\mathbb {E}}_{g^*} \log f_v(X) \propto -{\mathbb {E}}_u h(X) \log f_v(X) = -D(v)\nonumber \\ \end{aligned}$$

(17)

where in the first step we have dropped the constant term ${\mathbb {E}}_{g^*} \log g^*(X)$ and in the second step have used the definition of $g^*$ and dropped the constant factor 1 / l.

The objective is to maximise D(v) with respect to v (the parameters of the important sampling or proposal density). For this we need to compute D(v) which involves an expectation with respect to the distribution $f_u$. We can use again importance sampling to compute this expectation value. Instead of $f_u$ we sample from $f_w$ for some w. We thus obtain

$$\begin{aligned} D(v)={\mathbb {E}}_{w} h(X) \frac{f_u(X)}{f_w(X)}\log f_v(X) \end{aligned}$$

We estimate the expectation value by drawing N samples from $f_w$. If D is convex and differentiable with respect to v, the optimal v is given by

$$\begin{aligned} \frac{1}{N}\sum _{i=1}^N h(X_i) \frac{f_u(X_i)}{f_w(X_i)}\frac{d}{dv} \log f_v(X_i)=0\qquad X_i \sim f_w \end{aligned}$$

(18)

The cross entropy method considers the following iteration scheme. Initialize $w_0=u$. In iteration $n=0,1,\ldots$ generate N samples from $f_{w_n}$ and compute v by solving Eq. 18. Set $w_{n+1}=v$.

We illustrate the cross entropy method for a simple example. Consider ${\mathcal {X}}={\mathbb {R}}$ and the family of so-called tilted distributions $f_v(x)=\frac{1}{N_v} p(x)e^{vx}$, with p(x) a given distribution and $N_v=\int dx p(x)e^{vx}$ the normalisation constant. We assume that it is easy to sample from $f_v$ for any value of v. Choose $u=0$, then the objective Eq. 14 is to compute $l=\int dx p(x) h(x)$. We wish to estimate l as efficient as possible by optimising v. Eq. 18 becomes

$$\begin{aligned} \frac{\partial \log N_v}{\partial v}=\frac{ \sum _{i=1}^N h(X_i)e^{-w X_i}X_i }{\sum _{i=1}^N h(X_i) e^{-w X_i} } \end{aligned}$$

Note that the left hand side is equal to ${\mathbb {E}}_v X$ and the right hand side is the ’h weighted’ expected X under p (using importance sampler $f_w$). The cross entropy update is to find v such that h-weighted expected X equals ${\mathbb {E}}_v X$. This idea is known as moment matching: one finds v such that the moments of the left and right hand side, in this case only the first moment, are equal.

3.1 The Kullback–Leibler Formulation of the Path Integral Control Problem

In order to apply the cross entropy method to the path integral control theory, we reformulate the control problem Eq. 1 in terms of a KL divergence. Let ${\mathcal {X}}$ denote the space of continuous trajectories on the interval [t, T]: $\tau =X_{t:T}|x$ is a trajectory with fixed initial value $X(t)=x$. Denote $p_u(\tau )$ the distribution over trajectories $\tau$ with control u.

The distributions $p_u$ for different u are related to each other by the Girsanov theorem. We derive this relation by simply discretising time as before. In the limit $ds\rightarrow 0$, the conditional probability of $X_{s+ds}$ given $X_s$ is Gaussian with mean $\mu _s=X_s+f(s,X_s)ds+g(s,X_s)u(s,x_s)ds$ and variance $\Xi _sds=g(s,X_s)^2 ds$. Therefore, the conditional probability of a trajectory $\tau =X_{t:T}|x$ is²

$$\begin{aligned} p_u(\tau )= & {} \lim _{ds\rightarrow 0}\prod _{s=t}^{T-ds} {\mathcal {N}}(X_{s+ds}|\mu _s,\Xi _s)\nonumber \\= & {} p_0(\tau ) \exp \left( -\int _{t}^T ds \frac{1}{2}u^2(s,X_s)+\int _{t}^T u(s,X_s) g(s,X_s)^{-1} (dX_s-f(s,X_s)ds)\right) \nonumber \\ \end{aligned}$$

(19)

$p_0(\tau )$ is the distribution over trajectories in the absence of control, which we call the uncontrolled dynamics. Using Eq. 19 one immediately sees that

$$\begin{aligned} \int d\tau p_u(\tau ) \log \frac{p_u(\tau )}{p_0(\tau )}={\mathbb {E}}_u \int _t^T ds \frac{1}{2} u(s,X(s))^2 \end{aligned}$$

where we used that $dX_s-f(s,X_s)ds= g(s,X_s)\left( u(s,X_s) ds+dW_s\right)$. In other words, the quadratic control cost in the path integral control problem Eq. 3 can be expressed as a KL divergence between the distribution over trajectories under control u and the distribution over trajectories under the uncontrolled dynamics. Equation 3 can thus be written as

$$\begin{aligned} J(t,x)= & {} \min _u \int d\tau p_u(\tau ) \left( \log \frac{p_u(\tau )}{p_0(\tau )}+V(\tau )\right) \end{aligned}$$

(20)

with $V(\tau )=\Phi (X_T)+\int _t^T ds V(s,X(s))$. Since there is a one-to-one correspondence between u and $p_u$, one can replace the minimisation with respect to the functions u in Eq. 20 by a minimisation with respect to the distribution p subject to a normalisation constraint $\int d\tau p(\tau )=1$. The distribution $p^*(\tau )$ that minimises Eq. 20 is given by

$$\begin{aligned} p^*(\tau )=\frac{1}{\psi (t,x)} p_0(\tau )\exp (-V(\tau )) \end{aligned}$$

(21)

where $\psi (t,x)={\mathbb {E}}_{p_0} e^{-V(\tau )}$ is the normalisation, which is identical to Eq. 4. Substituting $p^*$ in Eq. 20 yields the familiar result $J(t,x)=-\log \psi (t,x)$.

Equation 21 expresses $p^*$ in terms of the uncontrolled dynamics $p_0$ and the path cost. From Eq. 19, we can equivalently express Eq. 21 in terms of the importance sampling distribution $p_u$ as

$$\begin{aligned} p^*(\tau )=\frac{1}{\psi (t,x)} p_u(\tau ) \exp (-S(t,x,u)) \end{aligned}$$

(22)

where S is defined in Eq. 2.

3.2 The Cross Entropy Method for Path Integral Control

We are now in a similar situation as the cross entropy method. We cannot compute the optimal control $u^*$ that parametrises the optimal distribution $p^*=p_{u^*}$ and instead wish to compute a near optimal control $\hat{u}$ such that $p_{\hat{u}}$ is close to $p^*$. Following the cross entropy (CE) argument, we minimise

$$\begin{aligned} KL(p^*|p_{\hat{u}})\propto & {} -{\mathbb {E}}_{p^*}\log p_{\hat{u}} \nonumber \\\propto & {} {\mathbb {E}}_{p^*} \left( \int _t^T \frac{1}{2} \hat{u}^2(s,X_s) ds-\hat{u}(s,X_s)g(s,X_s)^{-1}(dX_s-f(s,X_s)ds)\right) \nonumber \\= & {} \frac{1}{\psi (t,x)}{\mathbb {E}}_{p_u}e^{-S(t,x,u)} \int _t^T ds \left( \frac{1}{2}\hat{u}(s,X(s))^2-\hat{u}(s,X(s))\left( u(s,X(s))+\frac{dW_s}{ds}\right) \right) \nonumber \\ \end{aligned}$$

(23)

where in the second line we used Eq. 19 with $u=\hat{u}$ and discard the constant term ${\mathbb {E}}_{p^*} \log p_0$ and in the third line we used Eq. 22 to express ${\mathbb {E}}_{p^*}$ in terms of a weighted expectation with respect to an arbitrary distribution $p_u$ controlled by u. The KL divergence Eq. 23 must be minimised with respect to the functions $\hat{u}_{t:T}=\{\hat{u}(s,X_s), t\le s\le T\}$. We now assume that $\hat{u}(s,x|\hat{\theta })$ is a parametrised function with parameters $\hat{\theta }$. The KL divergence is a non-linear function of $\hat{\theta }$ that we can minimise by any gradient based procedure. The gradient of the KL divergence Eq. 23 is given by:

$$\begin{aligned} \frac{\partial KL(p^*|p_{\hat{u}})}{\partial \hat{\theta }}= & {} \left< \int _t^T \left( \hat{u}(s,X(s))ds-u(s,X(s))ds-dW_s\right) \frac{\partial \hat{u}(s,X(s))}{\partial \hat{\theta }} \right>_u \end{aligned}$$

(24)

$$\begin{aligned}= & {} -\left< \int _t^T dW_s\frac{\partial \hat{u}(s,X(s))}{\partial \hat{\theta }} \right>_{\hat{u}} \end{aligned}$$

(25)

where we introduce the notation $\left< F \right>_u=\frac{1}{\psi (x,t)}{\mathbb {E}}_{p_u}e^{-S(t,x,u)}F(\tau )$.

All components of the gradient can be estimated simultaneously by importance sampling. Equation 24 is the gradient in the point $\hat{u}$ for arbitrary importance sampler u. It is expected that the importance sampler $\hat{u}$ improves in each iteration. Therefore, the current estimate of the control function $\hat{u}(s,x|\hat{\theta })$ may provide a good candidate as importance sampler u, which gives Eq. 24. The gradient descent update at iteration n becomes in this case

$$\begin{aligned} \hat{\theta }_{n+1}= & {} \hat{\theta }_{n} - \eta \frac{\partial KL(p^*|p_{\hat{u}})}{\partial \hat{\theta }_{n}}=\hat{\theta }_{n} +\eta \left< \int _t^T dW_s \frac{\partial \hat{u}(s,X(s))}{\partial \hat{\theta }_{n}} \right>_{\hat{u}} \end{aligned}$$

(26)

with $\eta >0$ a small parameter. This gradient descent procedure converges to a local minimum of the KL divergence Eq. 23, using standard arguments. We refer to this gradient method as the path integral cross entropy method or PICE.

Note, that the gradient Eq. 24 involves a stochastic integral over time. This reflects the fact that a change in $\hat{\theta }$ affects $\hat{u}(s,x|\hat{\theta })$ for all s. When the parametrisation is such that each $\hat{u}(s,x|\hat{\theta }_s)$ has its own set of parameters $\theta _s$ for each s, the integral disappears in the gradient $\frac{\partial KL(p^*|p_{\hat{u}})}{\partial \hat{\theta }_s}$ .

Although in principle the optimal control for a finite horizon problem explicitly depends on time, there may be reasons to compute a control function $\hat{u}(x)$ that does not explicitly depend on time. For instance, when the horizon time is very large, and the dynamics and the cost are also not explicit functions of time. The advantage of a time-independent control solution is that it is simpler. Computing a time independent controller in the PICE framework is a special case of Eq. 24 with $\hat{u}(s,x|\hat{\theta })=\hat{u}(x|\hat{\theta })$.

In the case where both u and $\hat{u}$ are linear combinations of a fixed set of K basis functions $h_{k}(t,x), k=1,\ldots , K$

$$\begin{aligned} u(s,x)=\sum _{k=1}^{K} \theta _{k} h_{k}(s,x)\quad \hat{u}(s,x)=\sum _{k=1}^{K} \hat{\theta }_{k} h_{k}(s,x)\quad t\le s\le T \end{aligned}$$

we can set the gradient Eq. 24 equal to zero and obtain a linear system of equations for $\hat{\theta }_k$:

$$\begin{aligned} \sum _{k'=1}^{K} \left( \hat{\theta }_{k'}-\theta _{k'}\right) \left< \int _t^{T} ds h_{k'}(s,X_s) h_{k}(s,X_s) \right>_u= \left< \int _t^{T} dW_{s}h_{k}(s,X_s) \right>_u\quad k=1,\ldots , K\nonumber \\ \end{aligned}$$

(27)

that we can solve as $\hat{\theta }=\theta +A^{-1}b$ with $A_{kk'}=\left< \int _t^{T} ds h_{k}(s,X_s)h_{k'}(s,X_s) \right>_u$ and $b_k=\left< \int _t^{T} dW_{s} h_{k}(s,X_s) \right>_u$. This should in principle give the solution in one iteration. However, sampling with the initial control function u(s, x) may be inefficient, so that the estimates of A, b are poor. A more accurate estimate is obtained by iterating this procedure several times, using at iteration n the importance sampler $u(s,x)=\hat{u}(s,x|\hat{\theta }_n)$ to re-estimate A, b

$$\begin{aligned} \hat{\theta }_{n+1}=\hat{\theta }_n +A_n^{-1}b_n \end{aligned}$$

(28)

with $A_n,b_n$ the estimates of A, b using importance sampler $\hat{u}(s,x|\hat{\theta }_n)$.

Finally, we mention the special case of time-dependent linear parametrisation. Write the label $k=(r,l)$ and $h_{k}(s,x)=\delta _{r}(s) h_{l}(x)$ with $r=1,\ldots ,(T-t)/\Delta t$ a time-discretization label, l a basis function label. $\Delta t$ is the time discretisation and $\delta _{r}(s)=1$ for $t+(r-1)\Delta t <s<t+r\Delta t$ and zero otherwise. Equation 27 decouples in independent equations, one for each r:

$$\begin{aligned} \sum _{l'}\left( \hat{\theta }_{r,l'}-\theta _{r,l'}\right) \left< \int _{(r-1)\Delta t}^{r\Delta t} ds h_{l'}(X_s)' h_{l}(X_s) \right>_u=\left< \int _{(r-1)\Delta t}^{r\Delta t} dW_{s} h_{l}(X_s) \right>_u \end{aligned}$$

(29)

When $\Delta t\rightarrow ds$ we recover the expression in [46].

4 Numerical Illustration

In this section, we illustrate PICE for two simple problems. Both cases are finite horizon control problems. Therefore, the optimal control is explicitly time-dependent. We restrict ourselves in these examples to learn time-independent control solutions. For a linear quadratic control problem, we consider a controller that is linear in the state and the parameters. We compare the result with the optimal solution. For the inverted pendulum control task, we consider a controller that is non-linear in both the state and the parameters.

Consider the finite horizon 1-dimensional linear quadratic control problem with dynamics and cost

$$\begin{aligned} dX(s)= & {} u(s,X(s))ds+dW(s)\qquad 0\le s\le T\\ C= & {} {\mathbb {E}}_u \int _0^T ds \frac{R}{2}u^2(s,X(s)) +\frac{Q}{2} X(s)^2 \end{aligned}$$

with ${\mathbb {E}}_u dW(s)^2 =\nu ds$. The optimal control solution can be shown to be a linear feed-back controller

$$\begin{aligned} u^*(s,x)= & {} -R^{-1}P(s)x\qquad P(s)= \sqrt{QR} \tanh \left( \sqrt{\frac{Q}{R}}(T-s)\right) \end{aligned}$$

For finite horizon, the optimal control explicitly depends on time, but for large T the optimal control becomes independent of t: $u^*(x)=-\sqrt{\frac{Q}{R}} x$. We estimate a time-independent feed-back controller of the form $\hat{u}(x)=\theta _1 + \theta _2 x$ using path integral learning rule Eq. 26. The result is shown in Fig. 1.

Fig. 1

Illustration of PICE Eq. 26 for a 1-dimensional linear quadratic control problem with $Q=2, R=1, \nu =0.1, T=5$. We used time discretisation $ds=0.01$ and generated 50 sample trajectories for each gradient computation all starting from $x=2$ and $\eta =0.1$. The top left plot shows $\theta _{1,2}$ as a function of gradient descent step. Top right shows effective sample size as a function of gradient descent step. Bottom left shows optimal cost to go J as a function of gradient descent step. Bottom right shows 50 sample trajectories in the last gradient descent iteration

Note, that $\theta _1,\theta _2$ rapidly approach their optimal values $0,-1.41$ (red and blue line). Under- estimation of $|\theta _1|$ is due to the finite horizon and the transient behaviour induced by the initial value of $X_0$, as can be checked by initialising $X_0$ from the stationary optimally controlled distribution around zero (results not shown). The top right plot shows the entropic sample size defined as the scaled entropy of the distribution: $ss=-\frac{1}{\log N}\sum _{i=1}^N \hat{w}_i \log \hat{w}_i$ and $\hat{w}_i=w_i/\hat{\psi }$ from Eq. 12, as a function of gradient descent step, which increases due to the improved sampling control.

As a second illustration we consider a simple inverted pendulum, that satisfies the dynamics

$$\begin{aligned} \ddot{\alpha }= -\cos \alpha + u \end{aligned}$$

where $\alpha$ is the angle that the pendulum makes with the horizontal, $\alpha =3\pi /2$ is the initial ’down’ position and $\alpha =\pi /2$ is the target ’up’ position, $-\cos \alpha$ is the force acting on the pendulum due to gravity. Introducing $x_1=\alpha ,x_2=\dot{\alpha }$ and adding noise, we write this system as

$$\begin{aligned} dX_i(s)= & {} f_i(X(s)) ds + g_i(u(s,X(s)+dW(s))\qquad 0\le s\le T, \quad i=1,2\\ f_1(x)= & {} x_2 \quad f_2(x)=-\cos x_1\quad g=(0,1)\\ C= & {} {\mathbb {E}}_u \int _0^T ds \frac{R}{2}u(s,X(s))^2+\frac{Q_1}{2}(\sin X_1(s) -1)^2 + \frac{Q_2}{2}X_2(s)^2 \end{aligned}$$

with ${\mathbb {E}}_u dW_s^2=\nu ds$ and $\nu$ the noise variance.

We estimate a time-independent feed-back controller $\hat{u}(x|\theta )$ using a radial basis function neural network

$$\begin{aligned} \hat{u}(x|\theta )=\sum _{k=1}^K \gamma _k f_k(x) \quad f_k(x)= & {} \exp \left( -\beta _{1,k}\sin ^2(\frac{1}{2}(x_1-\mu _{1,k}))-\frac{1}{2}\beta _{2,k} (x_2-\mu _{2,k})^2\right) \end{aligned}$$

with $\theta =\{\gamma _{1:K},\beta _{1:2,1:K},\mu _{1:2,1:K}\}$. Note, that $\hat{u}$ is a non-linear function of $\theta$ and x. The $\sin$ term is to ensure that $f_k$ is periodic in $x_1$.

Fig. 2

Illustration of gradient descent learning Eq. 26 for a second order inverted pendulum problem with $Q_1=4, Q_2=0.01, R=1, \nu =0.3, T=10$. We used time discretisation $ds=0.01$ and generated 10 sample trajectories for each gradient computation all starting from $(x_1,x_2)=(-\pi /2,0)\pm (0.05,0.05)$ and $\eta =0.05$, $K=25$. Left entropic sample size versus importance sampling iteration. Middle optimal control solution $\hat{u}(x_1,x_2)$ versus $x_1,x_2$ with $0\le x_1\le 2\pi$ and $-2\le x_2\le 2$. Right 10 sample trajectories $\sin (x_t)$ versus t under control $\hat{u}(\vec {x}|\theta ^*)$ after learning (Color figure online)

We use the path integral learning rule Eq. 26. The gradients are easily computed. Figure 2(left) shows that the effective sample size increases with importance sampling iteration and stabilises to approximately 60 %. Figure 2(middle) shows the solution $\hat{u}(x|\theta ^*)$ after 300 importance sampling iterations in the $(x_1,x_2)$ plane. White star is initial location $(3\pi /2,0)$ (pendulum pointing down, zero velocity) and red star is the target state $x=(\pi /2,0)$ (pendulum point up, zero velocity). The swing-up uses negative velocities only. Using different initial condition of $\theta$ other solutions $\theta ^*$ may be found with positive, negative or both swing-up controls (results not shown). There are two example trajectories shown. Note the green NW-SE ridge of low control values around the top (red star). These are states where the position deviates from the top position, but with a velocity directed towards the top. So in these states no control is required. In the orthogonal NE-SW direction, control is needed to balance the pendulum. Figure 2(right) shows examples of 10 controlled trajectories using $\hat{u}(x|\theta ^*)$, showing that the learned state feedback controller is able to swing-up and stabilise the inverted pendulum.

5 Bayesian System Identification: Potential for Neuroscience Data Analysis

In neuroscience, there is great interest for scalable inference methods, e.g. to estimate network connectivity from data or decoding of neural recordings. It is common to assume that there is an underlying physical process of hidden states that evolves over time, which is observed through noisy measurements. In order to extract information about the processes giving rise to these observation, or to estimate model parameters, one needs knowledge of the posterior distributions over these processes given the observations. See [33, and references therein] for a treatment of state-space models in the context of neuroscience and neuro-engineering.

The estimation of the latent state distribution conditioned on the observations is a computationally intractable problem. There are in principle two types of approaches to approximate this computation: one can use one of many variations of particle filtering–smoothing methods, see [6, 10, 24]. The advantage of these methods is that they can in principle represent the latent state distribution with arbitrary accuracy, given sufficient computational resources. A fundamental shortcoming of these methods is that they are very computationally intensive. The reason is that the estimated smoothing distribution relies heavily on the filtering distribution. For high dimensional problems these distributions may differ significantly which yields poor estimation accuracy in practice and/or very long computation times. A common approach to alleviate this problem is to combine the particle filtering with a (block) Gibbs sampling that generates new particle trajectories from the filtered trajectories. This approach was successfully applied in the case of calcium imaging to estimate the (unobserved) activity of individual neurone based on calcium measurements. These estimates are then used to estimate a sparse connectivity structure between the neurons [28].

An alternative class of methods is to use one of the many possible variational approximations [3, 31] where the latent state distribution is approximated by a simpler, often multi-variate Gaussian, distribution. This approach was first proposed for neuro-imaging by [14, 15] and is currently the dominant approach for fMRI and MEG/EEG [8].

Fig. 3

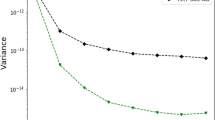
Comparison of path integral control (here denoted RPIIS) and the forward filter backward smoother (FFBSi cf. [24]) for a 2-dimensional neural network, showing mean and one standard deviation of the marginal posterior solution for both methods (Color figure online)

Here, we will illustrate the potential of path integral control methods to compute posterior distributions in time series models. We demonstrate how the main drawbacks of particle filtering can be overcome, yielding significant accuracy and speed-up improvements. One can easily see that the path integral control computation is mathematically equivalent to a Bayesian inference problem in a time series model with $p_{0}(\tau )$ the distribution over trajectories under the forward model Eq. 1 with $u=0$, and where one interprets $e^{-V(\tau )}=\prod _{s=t}^{T}p(y_{s}|x_{s})$ as the likelihood of the trajectory $\tau =x_{t:T}$ under some fictitious observation model $p(y_{s}|x_{s})=e^{-V(x_{s})}$ with given observations $y_{t:T}$. The posterior is then given by $p^{*}(\tau )$ in Eq. 21. One can generalise this by replacing the fixed initial state x by a prior distribution over the initial state. Therefore, the optimal control and importance sampling results of Sect. 3.2 can be directly applied. The advantage of the PI method is that the computation scales linear in the number of particles, compared to the state-of-the-art particle smoother that scales quadratic in the number of particles. In some cases significant accelerations can be made, e.g. [12, 24], but implementing these may be cumbersome [42].

To illustrate the path integral method for particle smoothing we estimate the posterior distribution of a noisy 2-dimensional firing rate model given 12 noisy observations of a single neuron, say $\nu _{1}$ (green diamonds in Fig. 3). The model is given by

$$\begin{aligned} \frac{d\nu _t}{dt}=-\nu _{t}+\tanh (J*\nu _{t}+\theta )+\sigma _{dyn}dW_{t} \end{aligned}$$

J is a 2-dimensional antisymmetric matrix and $\theta$ is a 2-dimensional vector, both with random entries from a Gaussian distribution with mean zero and standard deviation 25 and standard deviation 0.75, respectively, and $\sigma _{dyn}^{2}=0.2$. We assume a Gaussian observation model ${\mathcal {N}}(y_i|\nu _{1t_i},\sigma ^2_\mathrm {obs})$ with $\sigma _\mathrm {obs}=0.2$. We generate the 12 1-dimensional observations $y_i,i=1,\ldots , 12$ with $\nu _{1t_i}$ the firing rate of neuron 1 at time $t_i$ during one particular run of the model. We parametrised the control as $u(x,t)=A(t)x+b(t)$ and estimated the $2 \times 2$ matrix A(t) and the 2-dimensional vector b(t) as described in [46] or Eq. 29.

Estimates of the mean and variance of the marginal posterior distribution are shown in Fig. 3). The path integral control solution was computed using 22 importance sampling iterations with 6000 particles per iteration. As a comparison, the forward-backward particle filter solution (FFBSi) was computed using N = 6000 forward and M = 3600 backward particles. The computation time was 35.1 and 638 s, respectively. The results in Fig. 3 show that one effectively gets equivalent estimates of the posterior density over hidden neuronal states but in a fraction of the time using important sampling based upon optimal control.

Figure  4 shows the estimated control parameters used for the path integral control method. The open loop controller $b_1(t)$ steers the particles to the observations. The feedback controller $A_{11}(t)$ ’stabilises’ the particles around the observations (blue lines). Due to the coupling between the neurons, the non-observed neuron is also controlled in a non-trivial way (green lines). To appreciate the effect of using a feedback controller, we compared these results with an open-loop controller $u(x,t)=b(t)$. This reduces the ESS from 60 % for the feedback controller to around 29 % for the open loop controller. The lower sampling efficiency increases the error of the estimations, especially the variance of the posterior marginal (not shown).

Fig. 4

Control parameters; Left open-loop controller $b_i(t),i=1,2$; Right diagonal entries of feedback linear controller $A_{ii}(t),t=1,2$ (Color figure online)

The example shows the potential of adaptive importance sampling for posterior estimation in continuous state-space models. It shows that the controlled solution has high effective sample size and yields accurate estimates. Using a more complex controller yields higher sampling efficiency. There is in general a trade off between the accuracy of the resulting estimates and the computational effort involved to compute the controller. This method can be used to accelerate the E step in an EM procedure to compute the maximum likelihood estimates of model parameters, for instance connectivity, decoding of neural populations, estimation of spike rate functions and, in general, any inference problem in the context of state-space models; A publication with the analysis of this approach for high dimensional problems is under review [35].

6 Summary and Discussion

The original path integral control result of Theorem 1 expresses the optimal control $u^*(t,x)$ for a specific t, x as a Feynman–Kac path integral. $u^*(t,x)$ can be estimated using Monte Carlo sampling, and can be accelerated using importance sampling, using a sampling control. The efficiency of the sampling depends critically on the sampling control. This idea can be used very effectively for high dimensional stochastic control problems using the Model Predictive Control setting, where the optimal control is computed on-line for the current t, x [19].

However, Theorem 1 is of limited use when we wish to compute a parametrised control function for all t, x. We have therefore here proposed the cross entropy argument, originally formulated to optimise importance sampling distributions, to find a control function whose distribution over trajectories is closest to the optimally controlled distribution. In essence, this optimisation replaces the original KL divergence $KL(p|p^*)$ Eq. 20 by the reverse KL divergence $KL(p^*|p)$ and optimises for p. The resulting PICE method provides a flexible framework for learning a large class of non-linear stochastic optimal control problems with a control that is an arbitrary function of state and parameters. The idea to optimise this reverse KL divergence was earlier explored for the time-dependent case and linear feedback control in [17].

It is an important future research direction to apply PICE to larger control problems using larger models to represent the control and large number of samples. No matter how complex or high-dimensional the control problem, if the control solution approaches the optimal control sufficiently close, the effective sample size should reach 100 %. Representing the optimal control solution exactly requires in general an infinitely large model, except in special cases where a finite dimensional representation of the optimal control exists. Learning very large models requires very many samples to avoid overfitting. One can imagine a learning approach, where initially a simple model is learned (using limited data) to obtain an initial workable effective sampling size, and subsequently more and more complex models are learned using more data to further increase the quality of the control solution.

A key issue is the parametrisation that is used to represent $\hat{u}$. This representation should balance the two conflicting requirements of any learning problem: (1) the parametrisation should be sufficiently flexible to represent an arbitrary function and (2) the number of parameters should be not too large so that the function can be learned with not too many samples. Our present work extends the previous work of [50] to model the control using an arbitrary non-linear parametrisation. Neural networks are particularly useful in this context, since they are so-called universal approximators, meaning that any smooth function can be represented given enough hidden neurons. Reference [34] showed that the RBF architecture used in our numerical example is a universal approximator. Multi-layered perceptrons [2] and other deep neural networks are also universal approximators.

Reference [9] also discuss the application of the CE method to a Markov decision problem (MDP), which is a discrete state-action control problem. The main differences with the current paper are that we discuss the continuous state-action case. Secondly, [9] develops the CE method in the context of a discrete optimisation problem $x^*=\mathrm {argmax}_x f(x)$. They define a distribution p(x) and optimise the expected cost $C=\sum _x p(x) f(x)$ with respect to p. By construction, the optimal p is of the form $p(x)=\delta _{x,x^*}$, ie. a distribution that has all its probability mass on the optimal state.³ The CE optimisation computes this optimal zero entropy/zero temperature solution starting from an initial random (high entropy/high temperature) solution. As a result of this implicit annealing, it has been reported that the CE method applied to optimisation suffers from severe local minima problems [41]. An important difference for the path integral control problems that we discussed in the present paper is the presence of the entropy term $p(x) \log p(x)$ in the cost objective. As a result, the optimal p is a finite temperature solution that is not peaked at a single state but has finite entropy. Therefore, problems with local minima are expected to be less severe.

The path integral learning rule Eq. 26 has some similarity with the so-called policy gradient method for average reward reinforcement learning [40]

$$\begin{aligned} \Delta \theta =\eta {\mathbb {E}}_\pi \sum _a \frac{\partial \pi (a|s)}{\partial \theta }Q^\pi (s,a) \end{aligned}$$

where s, a are discrete states and actions, $\pi (a|s,\theta )$ is the policy which is the probability to choose action a in state s, and $\theta$ parametrises the policy. ${\mathbb {E}}_\pi$ denotes expectation with respect to the invariant distribution over states when using policy $\pi$ and $Q^{\pi }$ is the state-action value function (cost-to-go) using policy $\pi$. The convergence of the policy gradient rule is proven when the policy is an arbitrary function of the parameters.

The similarities between policy gradient and path integral learning are that the policy takes the role of the sampling control and the policy gradient involves an expectation with respect to the invariant distribution under the current policy, similar to the time integral in Eq. 26 for large T when the system is ergodic. The differences are (1) that the expectation value in the policy gradient is weighted by $Q^\pi$, which must be estimated independently, whereas the brackets in Eq. 26 involve a weighting with $e^{-S}$ which is readily available; (2) Eq. 26 involves an Itô stochastic integral whereas the policy gradient does not; (3) the policy gradient method is for discrete state and actions and the path integral learning is for controlled non-linear diffusion processes; (4) the expectation value used to evaluate the policy gradient is not independent of $\pi$ as is the case for the path integral gradients Eq. 24.

We have demonstrated that the path integral control method can be used to significantly improve the accuracy and efficiency of latent state estimation in time series models. These methods have the advantage that arbitrary accuracy can be obtained, but come at the price of significant computational cost. In contrast, variational methods have a fixed accuracy, but tend to be much faster. Based on the results presented in this paper, it is therefore interesting to compare variational methods and PICE directly for, for instance, fMRI data.

Appendix: Itô Calculus

Given two diffusion processes,

$$\begin{aligned} dY&= A(Y)ds + B(Y)dW \nonumber \\ dZ&= C(Z)ds + D(Z)dW \end{aligned}$$

(30)

the Itô’s product rule gives the evolution of the product process

$$\begin{aligned} d(YZ)&= YdZ + ZdY + d[Y,Z] \nonumber \\ d[Y,Z]&= B(Y)D(Z) ds \end{aligned}$$

(31)

The term in the last line is known as the quadratic covariance.

Let F(Y) as a function of the stochastic process Y. Itô’s Lemma is a type of chain rule that gives the evolution of F;

$$\begin{aligned} dF=dY \partial _y F + \frac{1}{2} d[Y,Y] \partial _y^2 F=\left( A\partial _y F +\frac{1}{2}B^2\partial _y^2 F\right) ds +B\partial _y F dW \end{aligned}$$

(32)

Putting a process Eq. 30 in integral notation and taking the expected value yields the following

$$\begin{aligned} Y&= \int Ads+ \int B dW \end{aligned}$$

(33)

$$\begin{aligned} {\mathbb {E}}_u[ Y ]&= \int {\mathbb {E}}_u[A] ds \end{aligned}$$

(34)

The Itô Isometry states that

$$\begin{aligned} {\mathbb {E}}_u\left[ \int A(Y)dW \int B(Y)dW \right]&= \int {\mathbb {E}}_u[A(Y)B(Y)] ds \end{aligned}$$

(35)