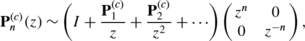Nonintersecting Brownian Motions on the Half-Line and Discrete Gaussian Orthogonal Polynomials

Abstract

We study the distribution of the maximal height of the outermost path in the model of N nonintersecting Brownian motions on the half-line as N→∞, showing that it converges in the proper scaling to the Tracy-Widom distribution for the largest eigenvalue of the Gaussian orthogonal ensemble. This is as expected from the viewpoint that the maximal height of the outermost path converges to the maximum of the Airy₂ process minus a parabola. Our proof is based on Riemann-Hilbert analysis of a system of discrete orthogonal polynomials with a Gaussian weight in the double scaling limit as this system approaches saturation. We consequently compute the asymptotics of the free energy and the reproducing kernel of the corresponding discrete orthogonal polynomial ensemble in the critical scaling in which the density of particles approaches saturation. Both of these results can be viewed as dual to the case in which the mean density of eigenvalues in a random matrix model is vanishing at one point.

Appendices

Appendix A: Proof of Lemmas 2.1 and 3.1

The proofs of Lemmas 2.1 and 3.1 are based on the following estimate of the rate of convergence of a Riemann sum, which is slightly sharper than the a priori rate of O(ε).

Lemma A.1

Let f(x ₁,…,x _n ) be an analytic function of n variables. Let the functions A _k (x ₁,…,x _n ) be defined recursively via

$$ A_{k}(x_1,\dots,x_n)=\sum _{j=1}^n \frac{\partial }{\partial {x}_j} A_{k-1}(x_1,\dots ,x_n), \qquad A_0 = f. $$

(A.1)

Suppose that

(A.2)

Then as ε→0,

$$ \int\cdots\int_{\mathbb {R}^n} f(x_1, \dots, x_n)\, dx_1 \cdots dx_n-\varepsilon ^n\sum _{x_1, \dots, x_n \in \varepsilon \mathbb {Z}}f(x_1, \dots, x_n)=O \bigl(\varepsilon ^4\bigr). $$

(A.3)

Proof

A multi-integral my be estimated by writing

(A.4)

Expanding each integrand on the RHS as a Taylor series and integrating term by term, this becomes

$$ \sum_{x_1, \dots, x_n \in \varepsilon \mathbb {Z}} \biggl[\varepsilon ^n f+ \frac{A_1}{2}\varepsilon ^{n+1}+\frac{A_2}{6}\varepsilon ^{n+2}+ \frac{A_3}{24}\varepsilon ^{n+3}+O\bigl(\varepsilon ^{n+4}\bigr) \biggr], $$

(A.5)

where

$$ f\equiv f(x_1,\dots,x_n), \qquad A_k\equiv A_j(x_1, \dots, x_n). $$

(A.6)

Thus the error in the Riemann sum is given by

$$ \begin{aligned}[b] & \int\cdots \int_{\mathbb {R}^n} f\, dx_1 \cdots dx_n-\sum_{x_1, \dots, x_n \in \varepsilon \mathbb {Z}} \varepsilon ^n f \\ &\quad =\varepsilon ^n \sum_{x_1, \dots, x_n \in \varepsilon \mathbb {Z}} \biggl[\frac{A_1}{2}\varepsilon +\frac{A_2}{6}\varepsilon ^{2}+ \frac{A_3}{24}\varepsilon ^{3}+O\bigl(\varepsilon ^{4}\bigr) \biggr] \\ &\quad = \biggl(\varepsilon ^n \sum_{x_1, \dots, x_n \in \varepsilon \mathbb {Z}} A_1 \biggr)\frac{\varepsilon }{2}+ \biggl(\varepsilon ^n \sum _{x_1, \dots, x_n \in \varepsilon \mathbb {Z}} A_2 \biggr)\frac{\varepsilon ^2}{6} \\ &\qquad{}+ \biggl(\varepsilon ^n \sum_{x_1, \dots, x_n \in \varepsilon \mathbb {Z}} A_3 \biggr)\frac{\varepsilon ^3}{24}+O\bigl(\varepsilon ^4\bigr). \end{aligned} $$

(A.7)

If (A.2) holds, then by the same argument,

$$ \begin{aligned}[c] \varepsilon ^n\sum _{x_1, \dots, x_n \in \varepsilon \mathbb {Z}} A_1(x_1, \dots, x_n)&=- \biggl(\varepsilon ^n \sum_{x_1, \dots, x_n \in \varepsilon \mathbb {Z}} A_2 \biggr)\frac{\varepsilon }{2}- \biggl(\varepsilon ^n \sum _{x_1, \dots, x_n \in \varepsilon \mathbb {Z}} A_3 \biggr)\frac{\varepsilon ^2}{6}+O \bigl(\varepsilon ^3\bigr), \\ \varepsilon ^n\sum_{x_1, \dots, x_n \in \varepsilon \mathbb {Z}} A_2(x_1, \dots, x_n)&=- \biggl(\varepsilon ^n \sum _{x_1, \dots, x_n \in \varepsilon \mathbb {Z}} A_3 \biggr)\frac{\varepsilon }{2}+O\bigl( \varepsilon ^2\bigr), \end{aligned} $$

(A.8)

and (A.7) can be written as

(A.9)

 □

Let us first apply this result to the proof of Lemma 3.1. By rescaling we can write (1.34) as

(A.10)

where

$$ \varepsilon =\pi\sqrt{\frac{r}{2n}}. $$

(A.11)

We have here an explicit prefactor times a Riemann sum for the function

$$ f(x_1, \dots, x_n)=\prod_{1\le j < k \le n} (x_k -x_j)^2 \exp \Biggl\{ -\sum _{j=1}^n x_j^2 \Biggr\}, $$

(A.12)

which is exactly the integrand in (1.56). One may easily check then that

$$ \begin{aligned}[c] A_1(x_1, \dots, x_n)&=-2(x_1+\cdots+x_n)f(x_1, \dots, x_n), \\ A_2(x_1, \dots, x_n)&=2f(x_1, \dots, x_n) \bigl(2(x_1+\cdots+x_n)^2-n \bigr) \\ &=-2 \bigl(A_1(x_1, \dots, x_n) (x_1+\cdots+x_n)+nf(x_1, \dots,x_n) \bigr). \end{aligned} $$

(A.13)

It is easy to see that A ₁ has the symmetry A ₁(x ₁,…,x _n )=−A ₁(−x ₁,…,−x _n ), from which it follows that

$$ \int\cdots\int_{\mathbb {R}^n} A_1(x_1, \dots, x_n)\, dx_1 \cdots dx_n=0. $$

(A.14)

It is a simple exercise to integrate by parts to see that

$$ \int\cdots\int_{\mathbb {R}^n} A_2(x_1, \dots, x_n) \,dx_1 \cdots dx_n=0. $$

(A.15)

It then follows that as r→0,

$$ \begin{aligned}[b] Z_n^{(\mathit{DOPE})}(r)&= \biggl(\frac{2}{\pi^2 n r} \biggr)^{n^2/2} Z_n^{(\mathit{GUE})} \bigl(1+O\bigl(\varepsilon ^4\bigr) \bigr) \\ &= \biggl(\frac{2}{\pi^2 n r} \biggr)^{n^2/2} Z_n^{(\mathit{GUE})} \biggl(1+O \biggl(\frac{r^2}{n^2} \biggr) \biggr). \end{aligned} $$

(A.16)

Taking logarithms gives (3.2).

We now prove Lemma 2.1 in the absorbing case. The proof in the reflecting case is nearly identical. Using symmetry about the origin and a rescaling of (1.15), we get

$$ \begin{aligned}[b] \mathbb{P} \Bigl(\max_{0<t<1} b_N^{(\mathit{BE})}(t)<M \Bigr) =& \frac{2^{N(N+1)}}{N! \pi^{N/2} \prod_{k=0}^{N-1} (2k+1)!} \\ &{}\times \Biggl(\varepsilon ^N \sum_{\mathbf{x} \in(\varepsilon \mathbb {N})^N} \bigl(\Delta \bigl(\mathbf{x}^2\bigr) \bigr)^2 \Biggl(\prod _{j=1}^N x_j^2 \Biggr)\exp \Biggl\{-\sum_{j=1}^N x_j^2 \Biggr\} \Biggr), \end{aligned} $$

(A.17)

where

$$ \varepsilon =\frac{\pi}{M\sqrt{2}}. $$

(A.18)

We again have an explicit prefactor times a Riemann sum for the integral

$$ \int_0^\infty\cdots\int _0^\infty \bigl(\Delta \bigl(\mathbf{x}^2 \bigr) \bigr)^2 \Biggl(\prod_{j=1}^N x_j^2 \Biggr)\exp \Biggl\{-\sum _{j=1}^N x_j^2 \Biggr\} \,dx_1\cdots dx_N. $$

(A.19)

This integral is the partition function for the Laguerre unitary ensemble. Its value is known (see e.g., [24]), and it exactly cancels the prefactor, so that

$$ \lim_{M \to\infty} \mathbb{P} \Bigl(\max_{0<t<1} b_N(t)<M \Bigr)=1. $$

(A.20)

Lemma A.1 also holds for multi-integrals over $\mathbb {R}_{+}^{n}$, that is if we replace ℝⁿ with ℝ₊ and ℤ with ℕ, and we can thus use Lemma A.1 with

$$ f(x_1, \dots, x_N)= \bigl(\Delta \bigl(\mathbf{x}^2\bigr) \bigr)^2 \Biggl(\prod _{j=1}^N x_j^2 \Biggr)\exp \Biggl\{-\sum_{j=1}^N x_j^2 \Biggr\}. $$

(A.21)

It is not difficult to see that in this case the condition (A.2) is satisfied. Indeed, notice that for any j=1,2,…,N,

$$ \int_0^\infty \biggl( \frac{\partial }{\partial {x}_j} f(x_1, \dots, x_N) \biggr) \,dx_j = -f(x_1,\dots,x_{j-1},0,x_{j+1}, \dots,x_N)=0. $$

(A.22)

Furthermore, notice that

$$ \frac{\partial }{\partial {x}_j} f(x_1, \dots, x_N)=\exp \Biggl\{-\sum_{k=1}^N x_k^2 \Biggr\} \Biggl( \prod _{k=1}^N x_k \Biggr) P(x_1, \dots, x_N) $$

(A.23)

for some polynomial P. It follows that, for any j=1,2,…,N,

$$ A_1(x_1,\dots,x_{j-1},0,x_j, \dots,x_N)=0, $$

(A.24)

and thus

$$ \int_0^\infty \biggl( \frac{\partial }{\partial {x}_j} A_1(x_1, \dots, x_N) \biggr)\, dx_j = -A_1(x_1, \dots,x_{j-1},0,x_j,\dots,x_N)=0. $$

(A.25)

(A.22) and (A.25) imply (A.2), and thus Lemma A.1 applies. It follows that

$$ \mathbb{P} \Bigl(\max_{0<t<1} b_N^{(\mathit{BE})}(t)<M \Bigr) =1+O\bigl(\varepsilon ^4\bigr)=1+O\bigl(M^{-4}\bigr). $$

(A.26)

In the scaling $M=\sqrt{\frac{2N}{a}}$ this becomes, as a→0,

$$ \mathbb{P} \Bigl(\max_{0<t<1} b_N^{(\mathit{BE})}(t)<M \Bigr) =1+O\bigl(\varepsilon ^4\bigr)=1+O \biggl(\frac{a^2}{N^2} \biggr). $$

(A.27)

Taking the logarithm proves Lemma 2.1. □

Appendix B: Proof of Lemma 2.3

If the parameter a is such that

$$ a<1-n^{-\delta }, \quad0<\delta <\frac{2}{3}, $$

(B.1)

then by (1.45) and (4.50) the jump matrix for X _n (z) about the origin is exponentially small in n, and therefore the asymptotic expansion for X _n (z) comes from the jumps on the circles ∂D(±b,ε). We need to calculate this expansion up to an error of the order n ⁻³. Instead of doing this directly, which is rather tedious, let us proceed by comparing our discrete orthogonal polynomials with their continuous brethren, the monic scaled Hermite polynomials $\{P_{j}^{(c)}(x)\}_{j=0}^{\infty}$, for which we have exact formulas. These polynomials satisfy the orthogonality condition

$$ \int_{-\infty}^{\infty} P_j^{(c)}(x)P_k^{(c)}(x)e^{-n\frac{a\pi ^2x^2}{2}} \,dx=h_k^{(c)} \delta _{jk}. $$

(B.2)

The superscript (c) stands for continuous. The continuous orthogonal polynomials $P_{n}^{(c)}$ can be characterized in terms of the following Riemann-Hilbert problem. We seek a matrix $\mathbf{P}_{n}^{(c)}(z)$ satisfying the following properties.

• (1) $\mathbf{P}_{n}^{(c)}(z)$ is analytic on ℂ∖ℝ.

• (2) For any real x,

  

  (B.3)

• (3) As z→∞,

  

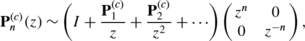  (B.4)

  where $\mathbf{P}^{(c)}_{k}$, k=1,2,… , are some constant 2×2 matrices.

This problem has the unique solution

(B.5)

The normalizing constants $h_{n}^{(c)}$ can be found as

$$ h_n^{(c)}=-2\pi i \bigl[\mathbf{P}^{(c)}_1 \bigr]_{12},\qquad \bigl(h_{n-1}^{(c)} \bigr)^{-1}=-\frac{ [\mathbf{P}^{(c)}_1 ]_{21}}{2\pi i}. $$

(B.6)

We can make a series of transformations to $\mathbf{P}_{n}^{(c)}$ to arrive at a small norm problem. Define $\mathbf{T}_{n}^{(c)}$ from the equation

$$ \mathbf{P}^{(c)}_n(z)=e^{\frac{nl}{2}\sigma_3}\mathbf{T}^{(c)}_n(z)e^{n(g(z)-\frac{l}{2})\sigma_3}, $$

(B.7)

and $\mathbf{S}_{n}^{(c)}$ as

(B.8)

Then the matrix $\mathbf{X}_{n}^{(c)}$ can be defined as

(B.9)

The jump matrices for $\mathbf{X}_{n}^{(c)}(z)$ are exponentially close to those for X _n (z), and therefore, by (4.85) and (4.86), $\mathbf{X}_{n}^{(c)}(z)$ and X _n (z) are exponentially close to each other. We are interested in the off diagonal terms of the matrix $\mathbf{X}_{1}^{(c)}$, where

$$ \mathbf{X}_n^{(c)}(z)=I+\frac{\mathbf{X}_1^{(c)}}{z}+O \bigl(z^{-2}\bigr). $$

(B.10)

One can easily see that

$$ \begin{aligned}[c] \bigl[\mathbf{X}_1^{(c)} \bigr]_{12}&= \bigl[\mathbf{P}_1^{(c)} \bigr]_{12}e^{-nl}-[\mathbf{M}_1]_{12} =-\frac{h_n^{(c)}}{2\pi i} \bigl(\pi^2 a e\bigr)^n - \frac{i}{\pi\sqrt{a}}, \\ \bigl[\mathbf{X}_1^{(c)} \bigr]_{21}&= \bigl[\mathbf{P}_1^{(c)} \bigr]_{21}e^{nl}-[ \mathbf{M}_1]_{21} =-\frac{2\pi i}{h_{n-1}^{(c)}(\pi^2 a e)^n}+\frac{i}{\pi\sqrt {a}}. \end{aligned} $$

(B.11)

The constants $h_{n}^{c}$ and $h_{n-1}^{(c)}$ are known exactly:

$$ h_{n}^{(c)}=\frac{n! \sqrt{2\pi}}{(\sqrt{na} \pi)^{2n+1}}, \qquad h_{n-1}^{(c)}=\frac{(n-1)! \sqrt{2\pi}}{(\sqrt{na} \pi)^{2n-1}}. $$

(B.12)

It follows that

$$ \begin{aligned}[c] & \bigl[\mathbf{X}_1^{(c)} \bigr]_{12}=- \frac{i}{\pi\sqrt{a}} \biggl(1- \biggl(\frac{e}{n} \biggr)^n \frac{n!}{\sqrt{2\pi n}} \biggr), \\ &\bigl[\mathbf{X}_1^{(c)} \bigr]_{21}=\frac{i}{\pi\sqrt{a}} \biggl(1- \biggl(\frac {n}{e} \biggr)^n\frac{\sqrt{2\pi}}{\sqrt{n} (n-1)!} \biggr). \end{aligned} $$

(B.13)

Applying Stirlings formula, we find that

$$ \begin{aligned}[c] \bigl[\mathbf{X}_1^{(c)} \bigr]_{12}=\frac{i}{\pi\sqrt{a}} \biggl(\frac {1}{12n}+ \frac{1}{288n^2} -\frac{139}{51840 n^3} +O\bigl(n^{-4}\bigr) \biggr), \\ \bigl[\mathbf{X}_1^{(c)} \bigr]_{21}= \frac{i}{\pi\sqrt{a}} \biggl(\frac {1}{12n}-\frac{1}{288n^2} - \frac{139}{51840 n^3} +O\bigl(n^{-4}\bigr) \biggr) . \end{aligned} $$

(B.14)

Let us now return to the discrete system of orthogonal polynomials. The normalizing constants are given as

$$ \begin{aligned}[c] h_{n,n}&=\frac{2}{\sqrt{a}} \biggl( \frac{1}{\pi^2 a e} \biggr)^n \bigl(1-[\mathbf{X}_1]_{12} \pi \sqrt{a} i \bigr) , \\ h_{n,n-1}^{-1}&=\frac{1}{2\sqrt{a}\pi^2} \bigl({\pi^2 a e} \bigr)^n \bigl(1+[\mathbf{X}_1]_{21}\pi \sqrt{a} i \bigr). \end{aligned} $$

(B.15)

Since X _n and $\mathbf{X}_{n}^{(c)}$ are exponentially close to each other, we may use the above expansion for X ₁, obtaining

$$ \begin{aligned}[c] h_{n,n}&=\frac{2}{\sqrt{a}} \biggl( \frac{1}{\pi^2 a e} \biggr)^n \biggl(1+\frac{1}{12n}+ \frac{1}{288n^2} -\frac{139}{51840 n^3} +O\bigl(n^{-4}\bigr) \biggr), \\ h_{n,n-1}^{-1}&=\frac{1}{2\sqrt{a}\pi^2} \bigl({\pi^2 a e} \bigr)^n \biggl(1-\frac{1}{12n}+\frac{1}{288n^2} + \frac{139}{51840 n^3} +O\bigl(n^{-4}\bigr) \biggr). \end{aligned} $$

(B.16)

Let us also note that in this asymptotic regime, by a similar argument, we find that the recurrence coefficients $A_{n,k}^{(\alpha )}(a)$ are exponentially close to zero, as they vanish for Hermite polynomials.

Appendix C: Deformation Equations for Orthogonal Polynomials

In this appendix, we prove the deformation equations (1.36) and (2.2). These equations are in fact quite general, and we present the proof for a general class of orthogonal polynomials. Let $\{p_{k}(x)\}_{k=0}^{\infty}$ be a system of monic polynomials satisfying the orthogonality condition

$$ \int_\mathbb {R}p_k(x)p_j(x)e^{-ax^2} \,d\mu(x)=h_k \delta _{jk}, $$

(C.1)

where dμ(x) is any measure on ℝ such that the system of orthogonal polynomials exists. We consider deformations of this system with respect to the parameter a. Let us write the three term recurrence equation, explicitly noting the dependence of each recurrence coefficient on the parameter a:

$$ xp_k(x)=p_{k+1}(x)+A_k(a)p_k(x)+B_k(a)p_{k-1}(x), \quad B_k(a)=\frac {h_k(a)}{h_{k-1}(a)}. $$

(C.2)

Notice that, since the polynomials p _k are monic, $\frac{\partial }{\partial a} p_{k}(x)$ is a polynomial of degree strictly less than k, and thus its integral against $p_{k}(x) e^{-ax^{2}}\, d\mu(x)$ is zero. Thus if we differentiate (C.1) with respect to a in the case j=k, apply the three term recurrence twice and integrate, we obtain

$$ h_k'(a)=-h_k (B_{k+1}+A_{k}+B_k ), $$

(C.3)

or equivalently

$$ \frac{\partial }{\partial a} \log h_k = -A_k- \frac{h_{k+1}}{h_k}- \frac {h_{k}}{h_{k-1}}, $$

(C.4)

where we have suppressed the notation which explicitly indicates dependence on a.

Let us use c _k,j to denote the coefficient of the x ^j term in the polynomial p _k (x), so that

$$ p_k(x)=x^k+c_{k,k-1} x^{n-1} +c_{k,k-2} x^{n-2}+ \cdots. $$

(C.5)

These coefficients depend on the parameter a, and by matching the coefficients of the x ^k term in (C.2), we see that

$$ A_k(a)=c_{k,k-1}-c_{k+1,k}. $$

(C.6)

To arrive at a deformation equation for A _k consider (C.1) with j=k−1. Differentiating with respect to a and disregarding the term for which the integral vanishes gives

$$ \int_\mathbb {R}\biggl[\frac{\partial }{\partial a} \bigl(p_k(x) \bigr) p_{k-1}(x) -x^2 p_{k-1}(x)p_k(x) \biggr]e^{-ax^2} \,d\mu(x)=0. $$

(C.7)

Applying the three term recursion twice and integrating, we obtain

$$ \biggl(\frac{\partial }{\partial a} c_{k,k-1} \biggr) h_{k-1}=A_kh_k+A_{k-1}B_k h_{k-1}. $$

(C.8)

Combining (C.6) with (C.8) both as it is written and with k↦k+1, we find

$$ A_k'(a)=B_k (A_k+A_{k-1} ) - B_{k+1} (A_{k+1}+A_{k}). $$

(C.9)

We now use (C.3) and (C.9) to differentiate (C.4) once more, obtaining

$$ \frac{\partial ^2}{\partial {a}^2} \log h_k=I_{k+1}-I_k, $$

(C.10)

where

$$ I_k=B_k \bigl(B_{k+1}+B_{k-1}+ (A_{k-1}+A_k )^2 \bigr). $$

(C.11)

It follows that the sum

$$ \sum_{k=0}^{n-1} \frac{\partial ^2}{\partial {a}^2} \log h_k $$

(C.12)

telescopes and its value is I _n −I ₀. But I ₀=0, and thus the sum (C.12) is simply I _n . After a change of variable, this proves (1.36).

We now prove (2.2). In the case that the measure of orthogonality is even, the recurrence coefficients A _k vanish, and we have

$$ I_k=B_kB_{k+1}+B_kB_{k-1} $$

(C.13)

and

$$ \begin{aligned}[c] &\sum_{k=0}^{N-1} \frac{\partial ^2}{\partial {a}^2} \log h_{2k}=\sum_{k=0}^{N-1} B_{2k+1}B_{2k+2}-B_{2k}B_{2k-1}; \\ &\sum _{k=0}^{n-1} \frac{\partial ^2}{\partial {a}^2} \log h_{2k+1}=\sum_{k=0}^{n-1} B_{2k+2}B_{2k+3}-B_{2k}B_{2k+1} \end{aligned} $$

(C.14)

which are again telescoping sums, and we obtain (2.2) after a change of variables.