Abstract
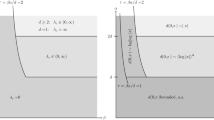
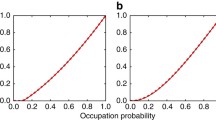
We derive percolation results in the continuum plane that lead to what appears to be a general tendency of many stochastic network models. Namely, when the selection mechanism according to which nodes are connected to each other, is sufficiently spread out, then a lower density of nodes, or on average fewer connections per node, are sufficient to obtain an unbounded connected component. We look at two different transformations that spread-out connections and decrease the critical percolation density while preserving the average node degree. Our results indicate that real networks can exploit the presence of spread-out and unreliable connections to achieve connectivity more easily, provided they can maintain the average number of functioningconnections per node.
Similar content being viewed by others
References
F. Baccelli B. Blaszczyszyn (2001) ArticleTitleOn a coverage process ranging from the boolean model to the Poisson Voronoi tassellation with application to wireless communications Adv. Appl. Probab. 33 IssueID2 293–323
P. Balister B. Bollobás M. Walters (2004) ArticleTitleContinuum percolation with steps in an annulus Ann. Appl. Probab. 14 IssueID4 1869–1879
L. Booth J. Bruck M. Franceschetti R. Meester (2003) ArticleTitleCovering algorithms, continuum percolation, and the geometry of wireless networks Ann. Appl. Probab. 13 IssueID2 722–741
O. Dousse, F. Baccelli, and P. Thiran, Impact of interferences on connectivity in ad-hoc networks, IEEE/ACM Trans. Network., in press.
D. Dubashi, O. Häggström, and A. Panconesi, Connectivity properties of bluetooth wireless networks, \emph{preprint}, http://www.math.chalmers.se/$\sim$ olleh/papers.html.
E. N. Gilbert (1961) ArticleTitleRandom plane networks J. SIAM 9 533–543
O. Häggström R. Meester (1996) ArticleTitleNearest neighbour and hard sphere models in continuum percolation Random Struct. Algor. 9 295–315
H. Kesten, Percolation Theory for Mathematicians Birkhäuser, (1982).
R. Meester and R. Roy, \emph{Continuum Percolation} (Cambridge University Press. 1996).
R. Meester M. D. Penrose A. Sarkar (1997) ArticleTitleThe random connection model in high dimensions Statist. Probab. Lett. 35 145–153
M. D. Penrose (1993) ArticleTitleOn the spread-out limit for bond and continuum percolation Ann. Appl. Probab. 3 IssueID1 253–276
T. K. Philips S. S. Panwar A. N. Tantawi (1989) ArticleTitleConnectivity properties of a packet radio network model IEEE Trans. Inf. Theory 35 IssueID5 1044–1047
J. Quintanilla S. Torquato R. M. Ziff (2000) ArticleTitleEfficient measurement of the percolation threshold for fully penetrable discs J. Phys. A: Math. General 33 L399–L407
J. Quintanilla S. Torquato (1997) ArticleTitleClustering in a continuum percolation model Adv. Appl. Probab. 29 327–336
G. Stell (1996) ArticleTitleContinuum theory of percolation J. Phys.: Condens. Matter 8 IssueID25A A1–A17
J. M. Gonzales-Barrios A. J. Quiroz (2003) ArticleTitleA clustering procedure based on the comparison between the k nearest neighbors graph and the minimal spanning tree Stat. Probab. Lett. 62 23–34
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Franceschetti, M., Booth, L., Cook, M. et al. Continuum Percolation with Unreliable and Spread-Out Connections. J Stat Phys 118, 721–734 (2005). https://doi.org/10.1007/s10955-004-8826-0
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/s10955-004-8826-0