Skip to main content
SpringerLink
Log in

Liquid–Liquid Equilibrium of Water + 1-Propanol or 1-Butanol + Dibutyl Ether Ternary Systems: Measurements and Correlation at Three Temperatures

  • Published:
Journal of Solution Chemistry Aims and scope Submit manuscript

Abstract

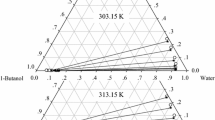
Liquid–liquid equilibrium (LLE) date for the ternary systems of {water + 1-propanol + dibutyl ether (DBE)} and (water + 1-butanol + DBE) were determined at T = (293.15, 303.15, 308.15) K under atmospheric pressure. Distribution coefficients and separation factors of 1-propanol in the mixtures were calculated and are discussed. The influence of temperature on the liquid phase regions was analyzed. In addition, the experimental values were correlated well with the modified and extended UNIQUAC models; the modified UNIQUAC model represents the data better than the extended UNIQUAC model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Tynjälä, P., Pakkanen, T.T., Mustamäki, S.: Modification of ZSM-5 zeolite with trimethyl phosphite. 2. Catalytic properties in the conversion of C1–C4 alcohols. J. Phys. Chem. B 102, 5280–5286 (1998)

    Article  Google Scholar 

  2. Demirel, Y.: Estimation of the entropy of vaporization at the normal boiling point for azeotropic mixtures containing water, alcohol or acetic acid. Thermochim. Acta 339, 79–85 (1999)

    Article  CAS  Google Scholar 

  3. Cháfer, A., de la Torre, J., Lladosa, E., Montón, J.B.: Liquid–liquid equilibria of 4-methyl-2-pentanone + 1-propanol or 2-propanol + water ternary systems: measurements and correlation at different temperatures. Fluid Phase Equilib. 361, 23–29 (2014)

    Article  Google Scholar 

  4. Çehreli, S., Özmen, D., Dramur, U.: (Liquid + liquid) equilibria of (water + 1-propanol + solvent) at T = 298.2 K. Fluid Phase Equilib. 239, 156–160 (2006)

    Article  Google Scholar 

  5. Ghanadzadeh, H., Ghanadzadeh, A., Bahrpaima, K.: Measurement and prediction of tie-line data for mixtures of (water + 1-propanol + diisopropyl ether): LLE diagrams as a function of temperature. Fluid Phase Equilib. 277, 126–130 (2009)

    Article  CAS  Google Scholar 

  6. Merzougui, A., Hasseine, A., Kabouche, A., Korichi, M.: LLE for the extraction of alcohol from aqueous solutions with diethyl ether and dichloromethane at 293.15 K, parameter estimation using a hybrid genetic based approach. Fluid Phase Equilib. 309, 161–167 (2011)

    Article  CAS  Google Scholar 

  7. Wypych, G.: Handbook of Solvents. ChemTec Publishing, Toronto (2001)

    Google Scholar 

  8. Wang, C., Guo, J., Cheng, K., Chen, Y.: Ternary (liquid + liquid) equilibria for the extraction of ethanol, or 2-propanol from aqueous solutions with 1,1′-oxybis (butane) at different temperatures. J. Chem. Thermodyn. 94, 119–126 (2016)

    Article  CAS  Google Scholar 

  9. Park, S.J., Hwang, I.C., Kwak, H.Y.: Binary liquid–liquid equilibrium (LLE) for dibutyl ether (DBE) + water from (288.15 to 318.15) K and ternary LLE for systems of DBE + C1–C4 alcohols + water at 298.15 K. J. Chem. Eng. Data 53, 2089–2094 (2008)

    Article  CAS  Google Scholar 

  10. Arce, A., Rodríguez, H., Rodríguez, O., Soto, A.: (Liquid + liquid) equilibrium of (dibutyl ether + methanol + water) at different temperatures. J. Chem. Thermodyn. 37, 1007–1012 (2005)

    Article  CAS  Google Scholar 

  11. Tamura, K., Chen, Y., Tada, K., Yamada, T., Nagata, I.: Representation of multicomponent liquid–liquid equilibria for aqueous and organic solutions using a modified UNIQUAC model. J. Solution Chem. 29, 463–488 (2000)

    Article  CAS  Google Scholar 

  12. Nagata, I.: Modification of the extended UNIQUAC model for correlating quaternary liquid–liquid equilibria data. Fluid Phase Equilib. 54, 191–206 (1990)

    Article  CAS  Google Scholar 

  13. Barton, A.F.M. (ed): IUPAC Solubility Data Series, Vol. 15. Alcohols with Water. Pergamon Press (1984) https://srdata.nist.gov/solubility/ Accessed March 8, 2018

  14. Stephenson, R., Stuart, J.: Mutual binary solubilities: water–alcohols and water–esters. J. Chem. Eng. Data 31, 56–70 (1986)

    Article  CAS  Google Scholar 

  15. Pirahmadi, F., Dehghani, M.R., Behzadi, B.: Experimental and theoretical study on liquid–liquid equilibrium of 1-butanol + water + NH4Cl at 298.15, 308.15 and 318.15 K. Fluid Phase Equilib. 325, 1–5 (2012)

    Article  CAS  Google Scholar 

  16. Sørensen, J.M., Arlt, W.: Liquid–liquid equilibrium data collection. Vol. V, Part 1. DECHEMA, Frankfurt/Main (1980)

  17. Prausnitz, J.M., Anderson, T.F., Grens, E.A., Eckert, C.A., Hsieh, R., O’Connell, J.P.: Computer Calculations for Multicomponent Vapor-Liquid and Liquid–Liquid Equilibria. Prentice Hall, Englewood Cliffs (1980)

    Google Scholar 

  18. Orchillés, A.V., Miguel, P.J., Vercher, E., Martínez-Andreu, A.: Isobaric vapor–liquid equilibria for methyl acetate + methanol + 1-ethyl-3-methylimidazolium trifluoromethanesulfonate at 100 kPa. J. Chem. Eng. Data 52, 915–920 (2007)

    Article  Google Scholar 

  19. Lepori, L., Matteoli, E., Bernazzani, L., Ceccanti, N., Conti, G., Gianni, P., Mollica, V., Tinè, M.R.: Isothermal vapour/liquid equilibria of binary mixtures with dibutyl ether at 298.15 K. Phys. Chem. Chem. Phys. 2, 4837–4842 (2000)

    Article  CAS  Google Scholar 

  20. Chen, Y., Wang, H., Tang, Y.Y., Zeng, J.: Ternary (liquid + liquid) equilibria for (water + 2-propanol + α-pinene, or β-pinene) mixtures at four temperatures. J. Chem. Thermodyn. 51, 144–149 (2012)

    Article  CAS  Google Scholar 

  21. Nelder, J.A., Mead, R.A.: simplex method for function minimization. Comput. J. 7, 308–313 (1965)

    Article  Google Scholar 

Download references

Funding

The authors thank the financial support from National Scientific Research Found of China (21271088).

Author information

Authors and Affiliations

  1. Department of Chemistry, Jinan University, Guangzhou, 510632, People’s Republic of China

    Wanxia Feng, Quanzhou Zhang & Yao Chen

Authors
  1. Wanxia Feng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Quanzhou Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yao Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yao Chen.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Feng, W., Zhang, Q. & Chen, Y. Liquid–Liquid Equilibrium of Water + 1-Propanol or 1-Butanol + Dibutyl Ether Ternary Systems: Measurements and Correlation at Three Temperatures. J Solution Chem 47, 498–510 (2018). https://doi.org/10.1007/s10953-018-0733-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10953-018-0733-0

Keywords

Search

Navigation