Skip to main content
SpringerLink
Log in

Measurement and Correlation of Excess Molar Enthalpy of Binary Mixtures Containing Butyl Acetate + 1-Alkanols (C1–C6) at 298.15 K

  • Published:
Journal of Solution Chemistry Aims and scope Submit manuscript

Abstract

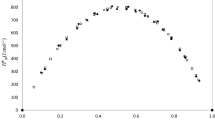
Excess molar enthalpies, ∆H Em , for the binary mixtures of butyl acetate + 1-alkanols, namely (methanol, ethanol, 1-propanol, 1-butanol, 1-pentanol, and 1-hexanol), were measured over the whole range of composition at 298.15 K using a Parr 1455 solution calorimeter. The excess partial molar enthalpies, ∆H Em,i , were calculated from the experimental excess molar enthalpies using the Redlich–Kister polynomial equation. The sign of ∆H Em for all systems are positive because of the disruption of hydrogen bonding and dipole–dipole interactions in the alkanols and esters, respectively. The magnitude of the ∆H Em values increases with increasing alkyl chain length. The behavior of ∆H Em was analyzed in terms of the length of the alkanol chain, the nature and type of intermolecular interactions and the balance between positive and negative effects on deviations from ideality. The experimental excess molar enthalpy data have also been correlated using the Redlich–Kister and SSF equations and two local composition models (UNIQUAC and NRTL).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2

Similar content being viewed by others

Abbreviations

A k :

Adjustable parameters of Redlich–Kister equation

A i , B i :

Adjustable parameters of SSF equation

Δu 12, Δu 21 :

Adjustable parameters contained in the UNIQUAC model

Δg 12, Δg 21 :

Interaction energy parameters in the NRTL model

α 12 :

Nonrandomness parameter in the NRTL model

∆H Em :

Excess molar enthalpy

∆H Em,i :

Excess partial molar enthalpy

ρ :

Density

n D :

Refractive index

R :

Universal gas constant

T :

Kelvin temperature

x i :

Mole fraction of component i

q :

Structural parameters in the UNIQUAC model

σ:

Standard deviation

References

  1. Prausnitz, J.M., Lichtenthaler, R.N., de Azevedo, E.G.: Molecular Thermodynamics of Fluid Phase Equilibria, 3rd edn. Prentice-Hall PTR, Upper Saddle River (1999)

    Google Scholar 

  2. Iloukhani, H., Khanlarzadeh, K.: Volumetric properties for binary and ternary systems consist of 1-chlorobutane, n-butylamine and isobutanol at 298.15 K and ambient pressure with application of the Prigogine–Flory–Patterson theory (PFP) and ERAS-Model. Thermochim. Acta 502, 77–84 (2010)

    Article  CAS  Google Scholar 

  3. Khanlarzadeh, K., Iloukhani, H.: Application of ERAS-Model and Prigogine–Flory–Patterson theory to excess molar volumes for ternary mixtures of 2-chlorobutane (1) + butylacetate (2) + isobutanol (3) at T = 298.15 K. J. Chem. Thermodyn. 43, 1583–1590 (2011)

    Article  CAS  Google Scholar 

  4. Iloukhani, H., Khanlarzadeh, K.: Physicochemical properties of quaternary systems and comparison of different geometrical models. J. Chem. Eng. Data 11, 4244–4252 (2011)

    Article  Google Scholar 

  5. Iloukhani, H., Zarei, H.A.: Excess molar enthalpies of N, N-dimethylformamide + alkan-1-ols (C1–C6) at 298.15 K. J. Chem. Eng. Data 47, 195–197 (2002)

    Article  CAS  Google Scholar 

  6. Iloukhani, H., Fattahi, M.: Correlation of excess molar enthalpies of cyclopentanone (1) + 1-alkanols (C1–C5) (2) by Peng–Robinson–Stryjek–Vera equation of state and ERAS-model. J. Mol. Liq. 171, 37–42 (2012)

    Article  CAS  Google Scholar 

  7. Khanlarzadeh, K., Iloukhani, H.: Experimental and theoretical study on excess molar enthalpy of binary mixtures containing isobutanol (1) + alkan-1-ols (C1–C4) (2) at T = 298.15 K. J. Mol. Liq. 187, 24–29 (2013)

    Article  CAS  Google Scholar 

  8. Gao, H., Li, S., Yan, W.: Excess molar enthalpies of ethylacetoacetate + (methanol, + ethanol, + 1-propanol, and + 2-propanol) at T = (298.15, 313.15 and 328.15) K, p = (0.1 and 10.0 MPa). Fluid Phase Eqilib. 268, 34–38 (2008)

    Article  CAS  Google Scholar 

  9. Bravo-Sanchez, M.G., Iglesias-Silva, G.A., Estrada-Baltazar, A., Hall, K.R.: Densities and viscosities of binary mixtures of n-butanol with 2-butanol, isobutanol, and tert-butanol from (303.15 to 343.15) K. J. Chem. Eng. Data 55, 2310–2315 (2010)

    Article  CAS  Google Scholar 

  10. Sheu, Y.W., Tu, C.H.: Densities, viscosities, refractive indices, and surface tensions for 12 flavor esters from T = 288.15 K to T = 358.15 K. J. Chem. Eng. Data 50, 1706–1710 (2005)

    Article  CAS  Google Scholar 

  11. Matsuo, H., Tu, C.H., Wong, D.C.Y., Sawamura, S., Taniguchi, Y., Koga, Y.J.: Excess partial molar enthalpy of 1-propanol in 1-propanol–NaCl–H2O at 25°C: the effect of NaCl on molecular organization of H2O. Phys. Chem. B 103, 2981–2983 (1999)

    Article  CAS  Google Scholar 

  12. Westh, P., Koga, Y.: Intermolecular interactions in 2-butoxyethanol–DMSO–H2O. J. Phys. Chem. 100, 433–438 (1996)

    Article  CAS  Google Scholar 

  13. Matthew, T.P., Koga, Y.: Interactions in 1-propanol-(1,2- and 1,3-) propanediol–H2O: the effect of hydrophobic vs hydrophilic moiety on the molecular organization of H2O. J. Phys. Chem. B 106, 7090–7095 (2002)

    Google Scholar 

  14. Redlich, O.J., Kister, A.T.: Algebraic representation of thermodynamic properties and the classification of solutions. Ind. Eng. Chem. 40, 345–348 (1948)

    Article  Google Scholar 

  15. Rogalsky, M., Malanowski, S.: A new equation for correlation of vapour–liquid equilibrium data of strongly non-ideal mixtures. Fluid Phase Equilib. 1, 137–152 (1977)

    Article  Google Scholar 

  16. Abrams, D.S., Prausnitz, J.M.: Statistical thermodynamics of liquid mixtures: a new expression for the excess Gibs energy of partly or completely miscible systems. AIChE J. 21, 116–128 (1975)

    Article  CAS  Google Scholar 

  17. Renon, H., Prausnitz, J.M.: Vapor–liquid equilibrium. XI. A new expression for the excess free energy of mixing. AIChE J. 14, 135–144 (1968)

    Article  CAS  Google Scholar 

  18. Riddick, J.A., Bunger, W.B., Sakano, T.K.: Organic Solvents, 3rd edn. Wiley, New York (1970)

    Google Scholar 

  19. Landgren, M., McEachern, D., Olofsson, Q., Randzio, S., Sunner, S.: Evaluation of excess enthalpies from flow-calorimetric measurements of enthalpies of dilution using local approximation by polynomials. J. Chem. Thermodyn. 10, 847–854 (1978)

    Article  CAS  Google Scholar 

  20. Checoni, R.F., Francesconi, A.Z.: Measurement and correlation of excess molar enthalpy at various temperatures acetonitrile + diethylamine or s-butylamine mixtures. J. Therm. Anal. Calorim. 80, 295–301 (2005)

    Article  CAS  Google Scholar 

  21. Venkatesulu, D., Prabhakara, M.V., Veerana, D.R.: Excess enthalpies of 2-alkoxyethanols with trichloroethylene and tetrachloroethylene at 298.15 K. Thermochim. Acta 242, 33–39 (1994)

    Article  CAS  Google Scholar 

  22. MacMillan, W.G., Mayer, J.E.: Statistical thermodynamics of multicomponents systems. J. Chem. Phys. 48, 675–690 (1945)

    Google Scholar 

  23. Yan, X.H., Wang, Q., Chen, G.H., Han, S.J.: Azeotropes at elevated pressures for systems involving cyclohexane, 2-propanol, ethyl acetate, and butanone. J. Chem. Eng. Data 46, 1235–1238 (2001)

    Article  CAS  Google Scholar 

  24. Wang, F.A., Chen, H.S., Zhu, J.Q., Song, J.C., Wang, Z.C.: Estimation of excess enthalpy for binary systems. J. Chem. Eng. 85, 235–243 (2002)

    Article  CAS  Google Scholar 

Download references

Acknowledgments

The authors would like to thank the Bu-Ali Sina University for providing the necessary facilities to carry out the research.

Author information

Authors and Affiliations

  1. Department of Physical Chemistry, Faculty of Chemistry, Bu-Ali Sina University, Hamedan, Iran

    Khatereh Khanlarzadeh & Hossein Iloukhani

Authors
  1. Khatereh Khanlarzadeh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hossein Iloukhani
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hossein Iloukhani.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khanlarzadeh, K., Iloukhani, H. Measurement and Correlation of Excess Molar Enthalpy of Binary Mixtures Containing Butyl Acetate + 1-Alkanols (C1–C6) at 298.15 K. J Solution Chem 43, 1259–1269 (2014). https://doi.org/10.1007/s10953-014-0199-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10953-014-0199-7

Keywords

Search

Navigation