Combining two-stage stochastic programming and recoverable robustness to minimize the number of late jobs in the case of uncertain processing times

Abstract

Minimizing the number of late jobs on a single machine is a classic scheduling problem, which can be used to model the situation that from a set of potential customers, we have to select as many as possible whom we want to serve, while selling no to the other ones. This problem can be solved by Moore–Hodgson’s algorithm, provided that all data are deterministic. We consider a stochastic variant of this problem, where we assume that there is a small probability that the processing times differ from their standard values as a result of some kind of disturbance. When such a disturbance occurs, then we must apply some recovery action to make the solution feasible again. This leads us to the area of recoverable robustness, which handles this uncertainty by modeling each possible disturbance as a scenario; in each scenario, the initial solution must then be made feasible by applying a given, simple recovery algorithm to it. Since we cannot accept previously rejected customers, our only option is to reject customers that would have been served in the undisturbed case. Our problem therefore becomes to find a solution for the undisturbed case together with a feasible recovery to every possible disturbance. Our goal hereby is to maximize the expected number of served customers; we assume here that we know the probability that a given scenario occurs. In this respect, our problem falls outside the area of the ‘standard’ recoverable robustness, which contains the worst-case recovery cost as a component of the objective. Therefore, we consider our approach as a combination of two-stage stochastic programming and recoverable robustness. We show that this problem is $\mathcal{NP}$-hard in the ordinary sense even if there is only one scenario, and we present some sufficient conditions that allow us to find a part of the optimal solution in polynomial time. We further evaluate several solution methods to find an optimal solution, among which are dynamic programming, branch-and-bound, and branch-and-price.

1 Introduction

Consider a one-man firm that is specialized in serving clients, who issue requests for help. Each request introduces a job into the system; we assume that we know how much time it takes to execute this job and the time by which it should be finished. The goal is to serve as many clients as possible, that is, we want to minimize the number of rejected requests. At the end of the day, the schedule for the next day is made and the clients that cannot be served are contacted.

The above problem boils down to the well-known problem of minimizing the number of tardy jobs on a single machine, which was first described by Moore (1968). If all data are deterministic and known beforehand, then the problem can be solved in $O(n \log n)$ time. There is one complication, however: there is a small probability that the worker gets ill during the night. Fortunately, in that case, he can contact a colleague, who will serve as a replacement. This replacement worker is not identical, however, which implies that he might need more time to carry out some of the jobs; as a consequence, it may not be possible to feasibly serve all selected (accepted) clients. Since we assume that it is not possible to accept previously rejected clients, the only way out is then to reject one or more of the previously accepted clients.

The situation sketched above is a typical example of applying the concept of recoverable robustness introduced by Liebchen et al. (2009). The idea is to find a solution that is feasible for the undisturbed case together with a way to repair this solution if it becomes infeasible in case of a disturbance; the possible disturbances are given as a list of scenarios. The value of a solution is computed on basis of the cost of the undisturbed solution and the cost of the solutions that are obtained by the recovery algorithm for all possible disturbances.

In this paper, we consider the problem of minimizing the number of tardy jobs on a single machine, which is denoted as $1||\sum U_j$ in the three field notation scheme by Graham et al. (1979). In the original setting, we are given n jobs, which we denote by $J_1 , \ldots , J_n$ or simply by jobs $1, \ldots ,n$ if no confusion is possible. For each job $J_j$ $(j=1, \ldots , n)$, we know its processing time $p_j$ and its due date $d_j$. There is one machine, which is continuously available from time zero onwards, that must execute all jobs, where executing job $J_j$ requires an uninterrupted interval of length $p_j$ on the machine. When job j is completed at or before its due date, then job j is considered to be on time; the goal is to maximize the number of jobs that are completed on time, which is the same as minimizing the number of jobs that are completed late (and possibly do not get executed at all). This problem is equivalent to the one of accepting as many jobs as possible, where accepting a job implies that it must be completed on time; the remaining jobs are then rejected. We allow the possibility that some disturbance takes place, which may change the processing times. The list of possible disturbances is given; we assume that at most one disturbance will take place. From now on we say that each possible disturbance corresponds to the occurrence of a scenario. We use S to denote the set of scenarios, and we use $p_j^s$ to denote the processing time of job $J_j$ $(j=1, \ldots , n)$ in scenario s. When solving the problem, we have to find an initial solution first, after which it is revealed which scenario occurs, if any; given the scenario, we then have to adjust the initial solution to make it feasible again. As mentioned above, the only possible recovery that we can apply is to reject one or more jobs that were accepted in the initial solution. We assume that we know all data from the scheduling instance and all data of the scenarios together with the probability that a scenario occurs. We use $q^s$ $(s \in S)$ to denote the probability that scenario s occurs; the probability that there is no disturbance is denoted by $q^0$. We measure the quality of a solution by the expected number of on time jobs, which we want to maximize. Since using the expected value takes us outside the area of recoverable robustness, in which the worst-case cost over all scenarios is included in the objective function, our approach is a combination of two-stage stochastic programming and recoverable robustness. Therefore, we call this the Two-stage Programming Recoverable Robust Number of Tardy jobs problem, which we abbreviate by TPRRNT.

This paper is organized as follows. In Sect. 2, we give a short overview of the relevant literature. In Sect. 3, we show that even the problem with only one scenario and with a common due date is $\mathcal{NP}$-hard in the weak sense. In Sect. 4, we present some dominance criteria that enable us to identify a subset of jobs that must be present in an optimal initial solution. In Sect. 5, we present several enumerative algorithms to solve this problem, which we test in Sect. 6.

Finally, in Sect. 7 we draw some conclusions and indicate some open problems.

Our contribution In this paper, we show that we can apply a combination of two-stage stochastic programming and recoverable robustness to deal with uncertainties in a number of single machine scheduling problems. This is the first result in this area, albeit that the multiple knapsack problem addressed by Tönissen et al. (2017) can be viewed upon as a multiple machine scheduling problem.

2 Literature

The single machine problem of minimizing the number of tardy jobs without disturbances, denoted as $1||\sum U_j$ in the scheduling literature, can be solved in $O(n \log n)$ by the algorithm by Moore–Hodgson, which from now on we shall refer to as algorithm MH. This algorithm starts with putting the jobs in order of non-decreasing due date, which yields the Earliest Due Date (EDD) schedule. Then, it iteratively scans the current schedule to find the first job that is late; it if finds such a job, then it removes the longest job from the set of jobs containing the late job and all its predecessors in the schedule. Eventually, the set of on time jobs remains. Lin and Wang (2007) and Hoogeveen and T’kindt (2012) present an $O(n^2)$ algorithm, called the SPT-based algorithm, in which the jobs are added one by one to the on time set in shortest processing time order; if adding a job results in an infeasible set, then the job added last is removed. van den Akker and Hoogeveen (2004) present an overview of variants of the deterministic $1||\sum U_j$ problem including release dates, deadlines, etc. Only a very limited amount of work has been published on the stochastic variant of the problem. van den Akker and Hoogeveen (2008) and Trietsch and Baker (2008) consider the variant where the processing times follow some given probability distribution. Van den Akker and Hoogeveen show that when this probability distribution possesses some nice characteristics, then the problem of maximizing the number of jobs that are stochastically on time is solvable through Moore–Hodgson’s algorithm; a job is stochastically on time if it satisfies the chance-constraint that the probability that it is on time in a given schedule is greater than or equal to a given minimum success probability. Baker and Trietsch extend these results to instances in which the jobs have stochastically-ordered processing times. As far as we know, no results have been published on the variant of $1||\sum U_j$ in which the processing times may change due to some disturbance without following some specific probability distribution.

We want to apply a combination of two-stage stochastic programming and recoverable robustness to deal with these disturbances. The latter technique was introduced by Liebchen et al. (2009) for railway optimization, where it has gained a lot of attention since (see for example Cacchiani et al. 2008; Cicerone et al. 2009). The key property is that it uses a pre-described, fast, and simple recovery algorithm to make a solution feasible for a set of given scenarios. Recoverable robustness has evolved from stochastic programming (Birge and Louveaux 1997) and robust optimization (Ben-Tal et al. 2009). Robust optimization does not allow a solution to be changed to make it feasible if some disturbance occurs; hence, the solution must be capable of dealing with any kind of common disturbance, which is likely to result in a conservative solution. If for example in our problem we have that there are n scenarios, where scenario i $(i=1, \ldots , n)$ corresponds to the case that the processing time of job i becomes equal to its due date, then in case of robust optimization we can select only one job. In case of stochastic programming decisions are taken in two stages: in the first stage a part of the solution is constructed, which is completed in the second stage after the true data have been revealed. If we allow the possibility to adjust the first stage solution completely, then it is best to take no decision at all in the first stage and just select the optimal solution as soon as we know which scenario occurs. In practice, this is often not possible, and therefore we restrict the possible adjustments to making jobs late in the second stage that were early in the first stage; it is not possible to complete jobs on time that were late in the first stage. This reflects the idea that a job corresponds to a customer: if a job cannot be completed on time, then the customer will go away.

After the initial work in the area of railway optimization, recoverable robustness is starting to get applied in the area of combinatorial optimization. The most studied problem in this respect is the Knapsack problem. Bouman et al. (2011) and van den Akker et al. (2016) consider the problem in which the size of the knapsack is uncertain; infeasibilities can be recovered by removing items. Tönissen et al. (2017) generalize this to the multiple knapsack problem. Büsing et al. (2011a, b) consider the single knapsack problem with uncertain item weights; in both cases infeasibilities can be recovered by removing up to k items, whereas in the former paper up to l new items can be added as well. Álvarez-Miranda et al. (2015a) study the Facility Location problem, where all kinds of uncertainties can occur when some disaster strikes; infeasibilities can be recovered by opening new facilities and/or reassigning customers. Bouman et al. (2011) and van den Akker et al. (2016) consider the Demand Robust Shortest Path problem, which was introduced by Dhamdhere et al. (2005). The problem here is to buy edges in a given graph to connect a given source and the, yet unknown, sink, where the goal is to minimize the total cost of the edges bought. In the first stage, one can buy edges at a cheaper price, and when the sink gets revealed, one can buy the additionally needed edges at a higher price. This problem is closely related to the recoverable robust Two-level Network Design problem studied by Álvarez-Miranda et al. (2015b). Given a graph with a root node r one must decide which edges to prepare, and whether this should be done by installing primary or secondary technology. Eventually, each customer (located in a vertex) should be connected to the root node through a prepared path, but a path from the root to a primary customer should only use primary technology edges. In the first phase, when it is still unknown which customers are primary, one must select the edges to prepare, where one can choose between installing primary and secondary technology; in the second phase, when the primary customers are revealed, it is possible to upgrade secondary technology to primary technology.

On the one hand, our research falls in the area of recoverable robustness, since we use a pre-described recovery algorithm to make a first stage solution feasible. On the other hand, we assume that we know the probability with which each scenario occurs, and we want to minimize the expected number of late jobs, which is a typical feature of stochastic programming; in its purest form, recoverable robustness uses the worst-case cost as a component of the objective function. Therefore, we are working at the intersection of both areas.

3 NP-hardness

In this section we show that the TPRRNT problem is $\mathcal{NP}$-hard in the ordinary sense, even if all jobs have the same due date and there is only one scenario. Since we present a dynamic programming algorithm in Sect. 5 for the general case with a fixed number of scenarios that runs in pseudo-polynomial time, this settles the computational complexity of this problem.

Theorem 1

The problem of deciding whether for a given instance of TPRRNT there exists a solution with cost no more than a given threshold value y is $\mathcal{NP}$-complete in the weak sense.

Proof

We use a reduction from the Partition with equal cardinality problem, which from now on we will refer to as problem PEC; this problem is known to be $\mathcal{NP}$-complete in the ordinary sense. The PEC problem is defined as follows:

Given 2n non-negative integral values $a_1, \ldots , a_{2n}$, does there exist a subset S of the index-set $\{1, \ldots , 2n\}$ with cardinality n such that

$$\begin{aligned} \sum _{j \in S} a_j = \sum _{j=1}^{2n} a_j /2? \end{aligned}$$

Given any instance of PEC we construct the following special instance of TPRRNT with one scenario, which occurs with probability $q^1$. For each element $a_j$ we introduce a job j, and we have a special job 0; each job has due date $4nA+A$, where $A=\sum _{j=1}^{2n} a_j /2$. The processing time of job j $(j=1, \ldots , 2n)$ is equal to $p_j=4A-a_j$ in the undisturbed case, and it is equal to $p^1_j=4A+a_j$ in the scenario. Job 0 has processing time $p_0=2A$ and $p^1_0=4nA$ in the undisturbed and disturbed case, respectively. The threshold is equal to $y=n(1-q^1)+(n+1)q^1=n+q^1$, and the question is whether there exists a feasible solution with value no more than y.

We will show that a ‘yes’ answer to the instance of TPRRNT implies that the answer to the instance of PEC is affirmative as well. First, suppose that there exists a subset S that leads to ‘yes’ on PEC. A straightforward computation shows that if we accept all jobs in S together with job 0 in the initial solution and additionally reject job 0 in case of a disturbance, then we find a solution with value y.

Suppose next that there exists a feasible solution to the instance of TPRRNT with value no more than y. Because of the sizes of the processing times and the value of the due date, we know that at most n of the jobs ${1, \ldots , 2n}$ can be on time. Hence, to meet the threshold, the initial solution must contain exactly n of these jobs together with job 0, whereas job 0 gets discarded in case of a disturbance. Let S denote the set containing the indices of the jobs in $\{1, \ldots , 2n\}$ that are accepted in the initial solution. In the undisturbed case, the total processing time of the jobs in S and job 0 is equal to

$$\begin{aligned} p_0 + \sum _{j \in S} p_j = 2A + \sum _{j \in S} (4A-a_j)=(4n+2)A-\sum _{j \in S} a_j. \end{aligned}$$

Since this is no more than the common due date $4nA+A$, we find that $\sum _{j \in S} a_j \ge A$. Similarly, because of the feasibility of S for the disturbed case, we must have that

$$\begin{aligned} \sum _{j \in S} p^1_j = \sum _{j \in S} (4A+a_j)=4nA+\sum _{j \in S} a_j \le 4nA+A. \end{aligned}$$

Hence, we must have that $\sum _{j \in S} a_j \le A$ as well, from which we immediately derive that the indices in S imply a ‘yes’ solution to PEC. $\square$

4 Dominance rules

In this section we show that it may be possible to reduce the size of an instance of the TPRRNT problem in polynomial time by identifying a part of the solution to the initial instance. Before specifying the corresponding dominance rule, we start with two negative results by analyzing two candidate rules that do not work.

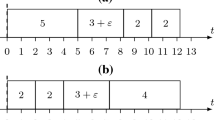
The negative results correspond to possible reduction rules that are based on solving the initial and scenario instance independently by algorithm MH. Suppose that in both solutions job j belongs to the on time set. As we will show by example, this does not have to imply that job j is part of the selected jobs in any optimal solution of the TPRRNT problem. In our example, we have 5 jobs, the data of which are found below.

	$J_1$	$J_2$	$J_3$	$J_4$	$J_5$
$d_j$	52	54	74	78	98
$p_j$	27	20	28	25	25
$p^1_j$	27	30	28	37	37

In the undisturbed case algorithm MH selects jobs $J_1, J_2, J_4, J_5$, and for the disturbed case algorithm MH selects jobs $J_1, J_3, J_5$. The only optimal solution of the TPRRNT problem, however, is to accept initially jobs $J_2, J_3, J_4, J_5$ and to reject $J_4$ in case of a disturbance.

The second obvious rule to reduce the size of the instance is to remove a job that is included neither in the schedule for the optimal solution, nor in the schedule for the scenario instance, when we apply algorithm MH to both instances independently. The example below shows that this rule is not correct in general.

	$J_1$	$J_2$	$J_3$	$J_4$	$J_5$
$d_j$	6	6	7	7	19
$p_j$	2	4	1	5	13
$p^1_j$	6	6	2	5	17

Algorithm MH will select jobs $J_1, J_2, J_3$ for the initial case and jobs $J_3, J_4$ for the scenario problem. The only optimum solution for TPRRNT, however, is to select the jobs $J_3, J_4, J_5$ initially and to reject job $J_5$ in the case of a disturbance.

Despite the first negative result, our dominance rule is based on identifying jobs that are selected by algorithm MH when applied to the initial case and scenario instance independently, but the selected jobs need to satisfy an additional criterion.

Definition 1

The set $H'$ contains the indices of the jobs that are included in the on time sets of the solutions obtained by algorithm MH for the initial case and for all scenario instances independently.

From this set $H'$ we select the subset H on basis of the Shortest Processing Time rule.

Definition 2

The set H is the subset of $H'$ of maximum cardinality such that for any job $J_j \in H$, we have that its processing time in the undisturbed situation and in each scenario is no more than the minimum processing times of all jobs not included in H in the corresponding situation. That is:

• $p_j \le p_i \quad \forall j \in H \text{ and } i \notin H$

• $p_j^s \le p_i^s \quad \forall j \in H, i \notin H \text{ and } \forall s \in S$.

To construct the set H from $H'$ we can use the following algorithm. We first put H equal to $H'$ and then check the constraints of the definition. If some job i fails the test, we remove it from H and run the test again, until we have reached a feasible set H. Remark that the order in which we remove the jobs from H does not matter, since we never add jobs to H; hence any job that fails the test will always fail, until it gets removed.

Theorem 2

For any instance of TPRRNT there exists an optimal solution in which the jobs in H are selected in the initial solution and in each one of the scenarios.

Proof

Consider any optimal solution to TPRRNT and suppose that not all jobs in H have been selected in the initial solution; let Q denote the jobs that have been selected in the optimal solution for the initial case. Now consider any job $j \in H$ such that $j \notin Q$. Since it is feasible to select all jobs in $H'$ by definition, Q must contain at least one job that does not belong to $H'$; from these jobs we choose the one with the smallest due date, which job we denote by $J_i$. We update our solution by replacing job $J_i$ with job $J_j$ in the set of selected jobs in the initial solution and in all scenarios.

We first show feasibility of the new initial solution. Suppose that $d_i \le d_j$. Let $\sigma$ denote the EDD schedule for the jobs in Q. If we simply replace $J_i$ with $J_j$ in $\sigma$ (leaving the order of the jobs intact), then we see that none of the completion times increase, because $p_i \ge p_j$. Moreover, we see that the completion time of $J_j$ will be no more than the completion time of $J_i$, which is no more than $d_i \le d_j$, and hence all jobs are on time. Now we consider the case $d_i > d_j$; we replace $J_i$ with $J_j$ and put the jobs in EDD order. Then, the completion times of the jobs before the original position of job $J_i$ may increase, but because of the choice of $J_i$ these are all jobs from H, and hence the resulting schedule must be feasible as well.

Now consider any scenario s. The current selection of on time jobs remains feasible, unless it contains $J_i$. In that case, we can show that replacing $J_i$ with $J_j$ yields a feasible solution by a proof following the same lines as the proof for the initial case. Hence, we find a solution with equal value that contains one more job from H. We repeat this procedure until all jobs in H have been included in the optimal solution for the initial case. The only thing left to show is that in each scenario solution all jobs in H are included. To that end, we apply the SPT-based algorithm to solve the $1||\sum U_j$ problem for each scenario s, where we restrict our instance to the jobs in the initial solution. Since the jobs in H have the smallest processing times, these are considered first by the SPT-based algorithm, and these will all be selected by definition of the set $H'$. $\square$

Even very minor changes in the processing times, which do not affect the SPT order of the jobs, can destroy all resemblance between the optimal solution, and the solutions obtained by algorithm MH for the initial and for all scenario instances independently, as shown by the example below with two scenarios. We conjecture that in the special case with only one scenario in which the order of the jobs does not change when the jobs are put in SPT order, then there exists an optimal solution in which all jobs in $H'$ belong to the initial solution.

	$J_1$	$J_2$	$J_3$	$J_4$
$d_j$	10	12	26	28
$p_j$	10	12	14	16
$p^1_j$	10	12	15	16
$p^2_j$	11	12	14	16

Algorithm MH finds the set $\{J_1, J_3\}$ for the initial case and the first scenario, and it finds the set $\{J_2, J_3\}$ for the second scenario, which implies that $H'=\{J_3\}$. The optimal solution to problem TPRRNT is to select jobs $J_2$ and $J_4$ initially and execute these in both scenarios.

5 Solution methods

In this section we will describe our solution methods for problem TPRRNT. We have applied dynamic programming, branch-and-bound, and branch-and-price. We compare these methods in the next section.

5.1 Dynamic programming

We first consider problem TPRRNT with a single scenario. Our dynamic programming algorithm is based on the algorithm by Lawler and Moore (1969) for the problem of minimizing the weighted number of late jobs. We add the jobs in Earliest Due Date order. We use state variables $f_j(r,t)$, which indicate the value of the optimal solution considering only jobs $J_1, \ldots , J_j$, where the total processing time of the selected jobs in the initial situation is r and the total processing time of the accepted jobs of the scenario schedule is t. We initialize the dynamic programming algorithm by putting $f_j(r, t) = 0$ if $j = r = t = 0$ and $+\,\infty$ otherwise. Each time we add a new job to the dynamic program, we have the choice between rejecting it in the initial solution, accepting it in the initial solution while rejecting it in the scenario solution, and accepting it in both. This leads to the following recurrence relation, in which $q^1$ is the probability that the scenario occurs.

$$\begin{aligned} f_{j+1}(r,t)= \left\{ \begin{array}{ll} \min \{f_j(r,t)+1, f_j(r-p_{j+1},t)+q^1, f_j(r-p_{j+1},t-p^1_{j+1}) \} &{} \quad \text{ if } r,t \le d_{j+1} \\ \infty &{}\quad \text{ otherwise } \end{array} \right. \end{aligned}$$

This dynamic programming algorithm has a running time of $O(n (\sum p_j )^2)$. Virtually, the same algorithm can be used to solve the weighted case through a simple adjustment of the recurrence relation, which then becomes

$$\begin{aligned} f_{j+1}(r,t)= \left\{ \begin{array}{ll} \min \{f_j(r,t)+w_j, f_j(r-p_{j+1},t)+q^1w_j, f_j(r-p_{j+1},t-p^1_{j+1}) \} &{}\quad \text{ if } r,t \le d_{j+1} \\ \infty &{}\quad \text{ otherwise } \end{array}\right. \end{aligned}$$

where $w_j$ denotes the weight of job j $(j=1, \ldots , n)$. Furthermore, this dynamic program can easily be modified to deal with the problem with more scenarios. We then have to extend the state variable to $f_j(r, t_1, \ldots , t_{|S|})$, where $t_i$ indicates the total processing time of the selected jobs for the ith $(i=1, \ldots , |S|$) scenario. In the recurrence relation, we then have to take the minimum over $2^{|S|}+1$ terms, since when we select job $j+1$ in the initial solution we have the possibility of accepting or rejecting job $j+1$ for each one of the |S| scenarios. This implies that the running time becomes exponential when |S| is not fixed. Even if |S| is fixed, then the dynamic programming algorithm will become very time consuming, because of its running time $O(nP^{|S|+1})$.

5.2 Branch-and-bound

Given an initial solution we can, for each scenario separately, determine the optimal recovery by applying algorithm MH to the jobs selected in the solution for the individual case. Hence, we only need to determine the initial solution, and therefore, we use as our branching strategy to either select or reject job j $(j=1, \ldots , n)$. To find a lower bound in a given node, we apply algorithm MH to the initial case and to all scenarios independently, while taking the constraints that describe the node into account. An initial upper bound can be found by solving the initial case by algorithm MH, after which we find the optimal recoveries for this initial solution by applying algorithm MH to the jobs contained in the initial solution for each scenario.

5.3 ILP: separate recovery decomposition

It is possible to formulate problem TPRRNT as an integer linear program using binary variables that indicate whether job j is selected or rejected in the initial solution and in the scenarios. To model and enforce the feasibility of the solution, we need so many constraints that it is only possible to solve small instances in this way. Therefore, we need a more intricate way to formulate and solve the problem as an ILP.

We will use the separate recovery decomposition model by Bouman et al. (2011). The approach is based on selecting one feasible set of accepted jobs for the initial case and one feasible set for each one of the scenarios; the feasibility of the combination of these sets will be enforced by constraints. Suppose that we know all feasible subsets for the initial case; we use R to denote this set of feasible subsets. We characterize subset $r \in R$ by binary parameters $u_{jr}$ that have value 1 if job j is not contained in it and zero otherwise. Similarly, we assume that we know the set $R_s$ containing all feasible subsets for scenario $(s \in S)$; we characterize feasible subset $r \in R_s$ for scenario s by binary parameters $u_{jr}^s$ similarly to $u_{jr}$. Furthermore, we introduce binary variables $x_r$ that indicate whether subset r is chosen for the initial case; similarly, we define binary variables $y_r^s$ that indicate whether subset r is chosen for scenario s. This leads to the following ILP formulation:

$$\begin{aligned} \min \quad q^0 \sum _{r \in R} \sum _{j=1}^n u_{jr}x_r + \sum _{s \in S} q^s \sum _{r \in R_s} \sum _{j=1}^n u^s_{jr}y^s_r \end{aligned}$$

subject to

$$\begin{aligned}&\sum _{r \in R} x_r =1 \end{aligned}$$

(1)

$$\begin{aligned}&\sum _{r \in R_s} y^s_r =1 \quad \forall s \in S\end{aligned}$$

(2)

$$\begin{aligned}&\sum _{r \in R} u_{jr}x_r - \sum _{r \in R_s} u^s_{jr} y^s_r \le 0 \quad \forall j=1,\ldots , n;\,\, \forall s \in S\\&x_r \in \{0,1\} \quad \forall r \in R \nonumber \\&y^s_r \in \{0,1\} \quad \forall r \in R_s;\,\, \forall s \in S\nonumber \end{aligned}$$

(3)

The constraints (3) enforce the connection between the initial subset and the subset selected in the scenarios: if $J_j$ is not part of the subset chosen for the initial case ($u_{jr}=1$), then this forces $u_{jr}^s=1$ for each scenario, implying that $J_j$ is not selected there as well. Since we do not want to enumerate the $O(2^n)$ possible subsets for the initial solution and for all scenarios, we solve this problem by applying the concept of column generation and branch-and-price. Thereto, we take the LP-relaxation, which we obtain by relaxing the integrality constraints to $x_r, y^s_r \ge 0$ [the upper bound of 1 on each variable is already enforced by the constraints (1) and (2)]. We solve this LP-relaxation for a small set of subsets that allow a feasible solution (for example the subset obtained by algorithm MH for the initial case together with the subsets for the scenarios obtained by applying algorithm MH to this selection), and from this we find the shadow prices that we need to compute the reduced cost of a new subset. Let $\lambda$, $\mu _s$, and $\pi _{js}$ denote the shadow prices corresponding to the constraints (1), (2), and (3), respectively. Then, we find that the reduced cost of subset r for the initial case is equal to

$$\begin{aligned}&q^0 \sum _{j=1}^n u_{jr}- \sum _{j=1}^n \sum _{s \in S} u_{jr}\pi _{js} -\lambda \\&\quad = \sum _{j=1}^n u_{jr} (q^0- \sum _{s \in S} \pi _{js}) -\lambda . \end{aligned}$$

Similarly, we can compute the reduced cost of subset r for a given scenario s; this is equal to

$$\begin{aligned} q^s \sum _{j=1}^n u^s_{jr}+ \sum _{j=1}^n u^s_{jr}\pi _{js} -\mu _s = \sum _{j=1}^n u^s_{jr} (q^s+ \pi _{js}) -\mu _s. \end{aligned}$$

As is well-known from LP-theory, we need to solve the pricing problem, which determines the subset with minimum reduced cost, for the initial case and for all scenarios. We only discuss the pricing problem for the initial case; the pricing problems for the scenarios are solved similarly. Since $\lambda$ is a constant, we must find a feasible set of binary values $u_{jr}$ that minimize

$$\begin{aligned} \sum _{j=1}^n u_{jr} (q^0- \sum _{s \in S} \pi _{js}). \end{aligned}$$

Since the subscript r is irrelevant, we drop this, and we further define $w_j= q^0- \sum _{s \in S} \pi _{js}$, for $j=1, \ldots , n$. Hence, we must find a feasible set of binary values $u_j$ $(j=1, \ldots , n)$ that minimize

$$\begin{aligned} \sum _{j=1}^n w_j u_j. \end{aligned}$$

Since putting $u_j=0$ implies that job j must be completed at or before its due date $d_j$, we find that the pricing problem boils down to the problem of minimizing the weighted number of tardy jobs on a single machine, which is solvable by the algorithm of Lawler and Moore (1969) in $O(n \sum p_j)$ time. If the outcome value of one or more of the pricing problems is negative, then we add the corresponding subset to the LP-relaxation and solve the LP again. When none of the pricing problems leads to a negative outcome value, we have solved the LP-relaxation to optimality. If the corresponding solution is integral, then we have found an optimal solution for the ILP as well. If there are fractional values, then we apply branch-and-price: this is a special type of branch-and-bound in which the lower bound in each node is determined by solving the LP-relaxation through column generation (see Barnhart et al. 1998). Just like in the case of the branch-and-bound of the previous subsection, we branch on the decision of accepting/rejecting job j $(j=1, \ldots , n)$ in the initial case. This branching strategy can easily be combined with the algorithm of Lawler and Moore to solve the pricing problems: if the job is rejected, then we remove it from the instance, and if it is accepted, then we have the freedom of deciding to include it in the subset for scenario s $(s \in S)$.

6 Computational results

We have performed extensive computational experiments to find out which algorithm works best and which settings give the best results. In Sect. 6.1, we describe how we create the problem instances. We first test the branch-and-bound and branch-and-price algorithms; see Sect. 6.2. These experiments are performed in two rounds. In the first round, we test both algorithms on instances with 40 jobs and 2 scenarios to find the best settings. In the second round, we increase the number of jobs and the number of scenarios to see how the performances of the best settings are affected. Next, we test the performance of dynamic programming algorithm; see Sect. 6.3. The problem and the algorithms are implemented using C#; we have solved the linear programs using ILOG CPLEX 12.6.0. All the experiments were run on an Intel core i7-3610QM 2.30 GHz processor with 8 GB of RAM. In the remainder, we only report on a part of the computational experiments; for a full report we refer to Stoef (2015).

6.1 Generating problem instances

We first generate the data for the initial, undisturbed case instances for the TPRRNT problem, after which we generate the data for the scenarios. The processing times are integers drawn from the uniform distribution U[1, 30]; given these, we compute $P=\sum p_j$. We then generate the due dates according to the scheme used by Potts and van Wassenhove (1985) for the similar problem of minimizing the total weighted tardiness on a single machine. They first choose values for two parameters, R and T, and then draw the due dates as integers from the uniform distribution $U[P(1-T-R/2), P(1-T+R/2)]$. For R and T, we try all values from $\{0.2, 0.4, 0.6, 0.8, 1\}$ for which $1-T-R/2 >0$; this leaves us with 14 different combinations.

Next we generate the scenario processing times. We construct four different instance types according to the following procedures. In all cases, we round the processing times to the nearest integer, if necessary.

• Random increase and decrease (RID) For each scenario $s \in S$ separately we draw $p_j^s$ using the following strategy: $p_j^s$ is equal to $p_j$, $0.75 p_j$, or $1.5 p_j$, all with probability one-third.

• Opposite increase and decrease (OID) This is comparable to (RID), but for each job $J_j$, we first determine randomly three subsets of scenarios with equal cardinality (if possible). Then, we put $p_j^s$ equal to $p_j$, $0.75 p_j$, and $1.5 p_j$ for all scenarios in the first, second, and third subset, respectively.

• Random increase (RI) Here, for each scenario $s \in S$ separately, we draw $p_j^s$ using the following strategy: $p_j^s$ is equal to $p_j$ in one-half of the cases and equal to $1.5 p_j$ in the remaining cases.

• Opposite increase (OI) This is comparable to RI, but the scenarios are first divided in two random groups with equal cardinality, similar to the procedure in OID.

If |S| is not a triple, then for OID we use RID in case of one remaining scenario, and in case of two remaining scenarios we let $p_j^s$ decrease in one and increase in the other. If |S| is odd, then for OI we use the RI strategy.

The probabilities for all scenarios are computed by randomly drawing a number from U[1, 3] after which we scale the probabilities.

6.2 Comparison of branching strategies

We first performed some initial experiments to find the optimal settings. For our branch-and-bound algorithm, we tested three types of node selection and five types of branching heuristics; 15 combinations in total. For node selection we tested Best First, Depth First, and Breadth First with Depth First as a clear winner. For our branching heuristic, we tested two selections based on due date (smallest and largest due date), two selections based on initial processing time (smallest and largest), and one in which we branch on a job that is rejected by the recovery algorithm. It turned out that branching on the largest job performed best with branching on the rejected job following closely. Therefore, we use in the remainder Depth First in combination with branching on the largest initial processing time.

Now we discuss the best settings for our implementation of branch-and-price. In each branch, we solve the LP-relaxation using column generation. We start the LP with only including the variables corresponding to the solution that algorithm MH finds for the initial case, and for the scenarios while taking the initial solution into account. In each iteration, we only add the column that corresponds to the optimal solution of a pricing problem, if it has negative reduced cost. After we have solved the LP-relaxation, we start the branching part, if necessary. We have tested the same settings as for the branch-and-bound algorithm, except for branching on the rejected job. The optimal setting is to branch on the longest job again, but in combination with Best First. We use Best First and branching on the longest job from now on in our computational experiments for branch-and-price.

Next we consider the difficulty of the instances. For each of the instance types (RID, OID, RI, OI), we generate 10 instances with $n=40$ and $s=2$ for each one of the 14 (R, T) combinations. We allow each instance to run for at most 3 minutes; we report ‘failed’ if it has not been solved by then, and we do not include these instances in the computation of the running times and number of nodes visited. The results are displayed in Tables 1 and 2. The column with header ‘integral’ in Table 2 indicates the number of instances for which the outcome of the LP-relaxation was integral (and hence no branching was necessary).

Table 1 Results for the different instance types for branch-and-bound

Table 2 Results for the different instance types for branch-and-price

For the branch-and-bound, it is obvious that the instance types RID and OID are most difficult. For the branch-and-price RID is most difficult, and then the picture becomes less clear: OID has fewer integral solutions than OI, but the average solution time of OI is higher, and 3 OI instances could not be solved in 3 minutes. Next we look at the influence of R and T, where we consider all four instance types. The results are displayed in Tables 3 and 4.

Table 3 Results for the different values of R and T for branch-and-bound

Table 4 Results for the different values of R and T for branch-and-price

For both solution procedures, the problem instances with $R=0.2$ and $T=0.6$ are the hardest to solve. To explain why the RID instances with $R=0.2$ and $T=0.6$ are most difficult, we have looked at the cardinality of the set H and at the difference between the lower bound and the optimal solution and the difference between the upper bound and the optimal solution. It is obvious that the larger |H|, the easier the problem becomes; similarly, the smaller the differences between the bounds, the easier the problem. Looking at our instances and the results of our experiments, we can draw the following conclusions.

• For all our instance types we find that when T increases, then |H| decreases, and the differences between the optimum value and the lower and upper bound increase for both branch-and-bound and branch-and-price, with the exception of $R=0.2$ and $T=0.8$.

• For all our instance types, we find that when R increases, then |H| increases; with respect to the differences between the optimum value and the lower and upper bound there is no clear picture.

• When comparing the instance types, we see, especially for the branch-and-bound algorithm, that the differences between the optimum value and the lower and upper bound are much larger for the RID and OID instances than for the RI and OI instances.

Our next step was to investigate the effect of an increase in the size of the instances. We generate the instances as described in Sect. 6.1. To study the effect of increasing the number of jobs, we have generated instances with $n=20, 40, 60, 80, 100, 120$ jobs and 2 scenarios; to study the effect of increasing the number of scenarios, we have generated instances with $n=40$ jobs and with $|S|=1,2,3,5,8,10$ scenarios. For each one of the four instance types, we generate 25 instances with random R and T value for each combination of n and |S|. We run these instances for at most 3 minutes; we use the optimal settings derived earlier.

We first look at the size of the set H. When we vary the number of jobs, then we observe a linear relation between n and |H|: approximately half of the jobs belongs to H. When we vary |S|, then we see that |H| drops sharply when |S| increases from 1 to 3, after which it more or less remains the same: on average |H| is approximately equal to 30 (out of 40) for $|S|=1$, this average drops to approximately 21 for $|S|=2$, and then remains approximately 17 for $|S| \ge 3$.

Next, we investigated the effect of n and |S| on the performance of branch-and-price. An increase of n leads to an exponential increase in the running time, number of columns, and number of iterations. The percentage of the instances for which the solution of the LP-relaxation is integral drops from almost 100% for $n=20$ to almost 50% for $n=120$. The running time, number of columns, and number of iterations all seem to scale linearly with the number of scenarios. The percentage of instances that are solvable without branching drops from almost 100% for $|S|=1$ to under 40% for $|S|=10$.

For the branch-and-bound algorithm, we see a similar behavior. The number of fails becomes equal for the larger instances, but branch-and-price solves more instances of the smaller problems. On the other hand, branch-and-price either solves the instances with 120 jobs in the root node, or it does not solve these at all. We see the same pattern when we increase the number of instances.

6.3 Dynamic programming

We test the dynamic programming algorithm on the same type of instances that we used to test the branching algorithms in the previous subsection. Because of the running time of $O(n P^{|S|+1})$, we only consider instances with $|S| \le 3$, and we reduce n when |S| increases. We consider instances with $n=5, 10, 15, 20, 30,40$ jobs and one scenario, instances with $n=5, 10, 15, 20$ jobs and two scenarios, and instances with $n=5$ jobs and three instances. We again generate 25 instances for each of the four instance types, and for each of the 14 R and T combinations. The results are not very encouraging to say the least: the 40 jobs instances with $|S|=1$ require 3.5 s on average, which is much more than the branching algorithms require on average for $n=40$ and $|S|=2$ (albeit that for the dynamic program only the size of P matters and small due dates only make the problem simpler). For $|S|=2$, 10 jobs was the maximum.

7 Conclusion

We have presented the first results in the area of stochastic scheduling with perturbations that result in deviations of the processing times that do not follow a given probability distribution function. To handle these disturbances, we were allowed to reject previously accepted customers as a recovery; therefore, we could apply the concept of recoverable robustness, which seems to be very well suited for handling disturbances in practical situations. Since we assume to know the probabilities with which each scenario occurs, we look at the expected value instead of the worst-case value, which leads to the combination of recoverable robustness and two-stage stochastic programming.

We have presented three types of algorithms to solve the problem: dynamic programming, branch-and-bound, and branch-and-price. Dynamic programming clearly performed worst; it is unclear which one of the branching algorithms is the winner. Since we believe that it is possible to improve our branch-and-bound through a tailored approach, and since the success of branch-and-price seems to depend on whether the problem is solved in the root node, we suggest to use branch-and-bound (which is also easier to implement).

Our dominance rule first of all seems to be very useful in reducing the size of the problem, but we can apply it to handle small changes in the due dates as well, provided that the EDD order remains the same for the undisturbed case and for all scenarios. If $d_j$ becomes one smaller in the scenario, then we can model this by including two dummy jobs that are immediately before and after $J_j$. The one before has processing time zero in the initial case and processing time one in the scenario, for the other dummy job this is just the opposite. Because of the small processing times, the dummy jobs will belong to set H, and hence these will be in the optimal solution, and their inclusion will effectively reduce $d_j$ by one.

There are two open questions left for our research. The first one is: what is the computational complexity of the problem with an arbitrary number of scenarios? The second one is whether we can guarantee that there exists an optimal initial solution that contains all jobs from $H'$ for the special case with only one scenario in which the order of the jobs is the same for the initial case and the scenario when the jobs are put in SPT order?

There are also several directions for future research. In our paper we minimize the expected value of a solution; the score on each scenario counts. An alternative evaluation of a solution is to use the score on the undisturbed situation together with the worst score on the scenarios. Much of our results, like the $\mathcal{NP}$-hardness, will go through unchanged, but we cannot use the separate recovery decomposition model anymore. A second research direction is to consider the variant of our problem in which the due dates may change, such that the EDD order for the undisturbed case and one or more of the scenarios becomes different. As algorithm MH strongly relies on the EDD order, this seems to be much more difficult. Finally, it might be worthwhile to look at the two-stage problem in which it is possible to accept costumers initially and to accept costumers when the scenario is revealed; obviously, the reward is bigger in the first case.