Abstract
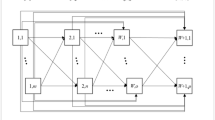
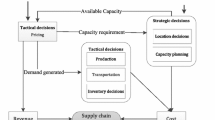
Due to the inevitable focus on core competencies, even small- and medium-sized companies are increasingly forced to form supply chain (SC) networks. However, their specific situation is often characterized by a lack of equity and limited access to capital markets, so that bank loans must then be used to initiate production and distribution. Within a short-term multi-day planning horizon, both operations and finance must be scheduled precisely in order to obtain practical instructions for each network partner and the network managers. For this purpose, continuous-time modeling is required. Additionally, a coordination of monetary consequences resulting from both site-specific operational events and network-wide financial transactions is necessary to prevent insolvency. As bank overdrafts can be used to overcome financial imbalances during short periods (e.g., days or even hours), appropriate time intervals for liquidity management should be determined. The implementation of these intervals requires discrete-time modeling. In this context, the main challenge is to combine both of the aforementioned modeling techniques within a common decision model. To address this problem, a novel mixed-integer nonlinear program (MINLP) is developed, which enables exact planning and scheduling of SC operations as well as related financial transactions on the one hand, and periodic liquidity balancing on the other hand. A numerical analysis was based on a test scenario with randomly generated data. As we found out that even small problem instances of the MINLP, e.g., a three-stage supply chain with three sites in each stage, were not computable with high-performance hardware and a commercial nonlinear standard solver, we additionally propose an equivalent linearized version of the decision model. The latter could be optimized within acceptable computation time using the CPLEX solver.





Similar content being viewed by others
References
Baumann, P., & Trautmann, N. (2013). A continuous-time MILP model for short-term scheduling of make-and-pack production processes. International Journal of Production Research, 51(6), 1707–1727.
Chang, Y.-C., Chang, K.-H., & Chang, T.-K. (2013). Applied column generation-based approach to solve supply chain scheduling problems. International Journal of Production Research, 51(13), 4070–4086.
Erengüç, Ş., Simpson, N. C., & Vakharia, A. J. (1999). Integrated production/distribution planning in supply chains: An invited review. European Journal of Operational Research, 115(2), 219–236.
Floudas, C. A., & Lin, X. (2004). Continuous-time versus discrete-time approaches for scheduling of chemical processes: A review. Computers and Chemical Engineering, 28, 2109–2129.
GAMS. (2015). GAMS documentation 24.5. Washington, DC: GAMS Development Corporation. http://www.gams.com/help/index.jsp.
Gomes, M. C., Barbosa-Póvoa, A., & Novais, A. Q. (2013). Reactive scheduling in a make-to-order flexible job shop with re-entrant process and assembly: A mathematical programming approach. International Journal of Production Research, 51(17), 5120–5141.
Guillén-Gosálbez, G., Badell, M., Espuña, A., & Puigjaner, L. (2006). Simultaneous optimization of process operations and financial decisions to enhance the integrated planning/scheduling of chemical supply chains. Computers & Chemical Engineering, 30, 421–436.
Günther, H. O. (2014). The block planning approach for continuous time-based dynamic lot sizing and scheduling. Business Research, 7(1), 51–76.
Hahn, G. J., & Kuhn, H. (2011). Value-based performance and risk management in supply chains: A robust optimization approach. International Journal of Production Economics, 139(1), 135–144.
Jayaraman, V., & Pirkul, H. (2001). Planning and coordination of production and distribution facilities for multiple commodities. European Journal of Operational Research, 133(2), 394–408.
Laínez, J. M., Guillén-Gosálbez, G., Badell, M., Espuña, A., & Puigjaner, L. (2007). Enhancing corporate value in the optimal design of chemical supply chains. Industrial & Engineering Chemistry Research, 46, 7739–7757.
Lee, Y. H., & Kim, S. H. (2002). Production–distribution planning in supply chain considering capacity constraints. Computers & Industrial Engineering, 43(1–2), 169–190.
Li, Z., & Ierapetritou, M. G. (2009). Integrated production planning and scheduling using a decomposition framework. Chemical Engineering Science, 64(16), 3585–3597.
Low, C., Li, R.-K., & Chang, C.-M. (2013). Integrated scheduling of production and delivery with time windows. International Journal of Production Research, 51(3), 897–909.
Martins, P., & Quelhas, A. P. (2016). Workforce planning and financing on a production/capital discrete-time model. International Transactions in Operational Research, 23, 507–538.
Mockus, L., & Reklaitis, G. V. (1999). Continuous time representation approach to batch and continuous process scheduling. 1. MINLP formulation. Industrial & Engineering Chemistry Research, 38, 197–203.
Mohammadi, G., Karampourhaghghi, A., & Samaei, F. (2012). A multi-objective optimisation model to integrating flexible process planning and scheduling based on hybrid multi-objective simulated annealing. International Journal of Production Research, 50(18), 5063–5076.
Moir, L. (1997). Managing liquidity (2nd ed.). Cambridge: Woodhead Publishing.
Mokhtari, H., Abadi, I. N. K., & Amin-Naseri, M. R. (2012). Production scheduling with outsourcing scenarios: A mixed integer programming and efficient solution procedure. International Journal of Production Research, 50(19), 5372–5395.
Park, Y. B. (2005). An integrated approach for production and distribution planning in supply chain management. International Journal of Production Research, 43(6), 1205–1224.
Shah, N. K., & Ierapetritou, M. G. (2012). Integrated production planning and scheduling optimization of multisite, multiproduct process industry. Computers and Chemical Engineering, 37, 214–226.
Steinrücke, M. (2011). An approach to integrate production–transportation planning and scheduling in an aluminium supply chain network. International Journal of Production Research, 49(21), 6559–6583.
Steinrücke, M. (2015). Integrated production, distribution and scheduling in the aluminium industry: A continuous-time MILP model and decomposition method. International Journal of Production Research, 53(19), 5912–5930.
Ullrich, C. A. (2013). Integrated machine scheduling and vehicle routing with time windows. European Journal of Operational Research, 227(1), 152–165.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Albrecht, W., Steinrücke, M. Continuous-time production, distribution and financial planning with periodic liquidity balancing. J Sched 20, 219–237 (2017). https://doi.org/10.1007/s10951-016-0488-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10951-016-0488-7