1 Introduction

Earthquake ground motions on the seafloor differ from onshore ground motions in vertical components and vertical-to-horizontal (V/H) response spectral ratios (Chen et al. 2015). The characteristics of offshore ground motion have been investigated by some investigators, and vertical offshore ground motion values have been found to be much lower than those of horizontal offshore ground motion (e.g., Boore and Smith 1999; Chen et al. 2017; Diao et al. 2014; Li et al. 2015); thus, the vertical-to-horizontal peak ground acceleration (PGA) and spectral ratios of offshore ground motions are considerably different from those of onshore ground motions.

Offshore stations are mainly located in the USA and Japan (e.g., the Earthquake and Tsunami Monitoring Cable (ETMC) of the K-NET in Sagami Bay (Eguchi et al. 1998), the Seafloor Earthquake Measuring System (SEMS) off the coast of southern California (Boore and Smith 1999), the Dense Ocean Network for Earthquake and Tsunamis (DONET) in the Nankai Trough in Japan (Kaneda et al. 2015), and the Seafloor Observation Network for Earthquakes and Tsunamis (S-net) along the Japan Trench (Kanazawa 2013)). Boore and Smith (1999) analyzed the V/H spectral ratios of Fourier amplitude spectra and response spectra for the offshore ground motion obtained from SEMS instruments. The offshore ground motion reported in their study showed very low-amplitude vertical components compared to those of the onshore motion and particularly for short periods; however, due to a lack of onshore records for distances comparable to those taken from sources to the SEMS sites, they did not present a direct comparison of offshore and onshore records. Diao et al. (2014) studied the effect of water layer on the vertical components of offshore ground motions via a theoretical method using the same offshore records employed by Boore and Smith (1999). They concluded that water layer can reduce the vertical component amplitudes of offshore ground motions, consistent with Boore and Smith (1999). Li et al. (2015) proposed a method for modeling and simulating the offshore ground motion, and their results showed that the vertical ground motions on the seafloor are suppressed near the P-wave resonant frequencies. Chen et al. (2015, 2017) selected eight earthquakes recorded by the Kyoshin network (K-NET) to analyze horizontal normalized response spectra and V/H response spectral ratios using 36 offshore records from six offshore stations throughout the Sagami Bay and 31 onshore records from eight onshore stations adjacent to those offshore stations. Their results revealed that the normalized response spectra and V/H response spectral ratios of the offshore ground motions were different from those of the onshore motions. Moreover, V/H ratios at short periods for the offshore ground motions were much lower than those for the onshore motions. Nevertheless, as they examined only a few earthquakes and 36 offshore records, they did not identify how explanatory variables, such as the magnitude and hypocentral distance, affect the V/H spectral ratios. Dhakal et al. (2017) processed 315 earthquakes recorded at the same six K-NET offshore stations to compute the mean S-wave horizontal-to-vertical (S-H/V) spectral ratios of weak ground motions and compared these to the S-H/V spectral ratios of strong ground motions. Their results indicated that the six offshore stations exhibited nonlinear responses during strong earthquakes and that the PGA threshold causing a nonlinear site response differed from site to site, mainly because the underlying site geology is not uniform beneath the offshore sites. We know from their study that the differences in V/H spectral ratios observed between the offshore stations are largely due to varying local site conditions. The ground motion prediction equation (GMPE) of offshore sites is different from that of onshore stations (Hu et al. 2020), and we have presented a direct comparison of V/H spectral ratios of the offshore and onshore ground motion, from which we can understand how V/H spectral ratios vary by period, moment magnitude, hypocentral distance, etc.

Prediction models for V/H spectral ratios of different onshore areas have been proposed by several researchers (e.g., Bommer et al. 2011; Gülerce and Abrahamson, 2011; Bozorgnia and Campbell 2016; Soghrat and Ziyaeifar 2016; Zolfaghari and Darzi 2019a) who have examined the relationships between horizontal and vertical components of onshore ground motions and pointed out that a prediction equation for V/H ratios is needed in the probabilistic seismic hazard analysis (PSHA). The V/H ratio can be estimated from independent GMPEs for vertical and horizontal components developed from the same dataset and functional forms (e.g., Boore et al. 2014; Stewart et al. 2016; Zolfaghari and Darzi 2019b). However, this approach cannot obtain the residuals and standard deviations of V/H ratios, and therefore, the direct estimation of V/H ratios using regression analysis from a ground motion dataset has been proposed (e.g., Zolfaghari and Darzi 2019b). Furthermore, Akkar et al. (2014) pointed out that the direct estimation of V/H ratios can preserve the better consistency between horizontal and vertical components than those obtained from independent horizontal and vertical GMPEs.

The American Petroleum Institute (API) showed that the seismic analysis of a fixed offshore platform should input a combination of vertical and horizontal ground motions and that a V/H ratio of 0.5 is recommended (RP2A-WSD 2014). Simplified period-dependent models for V/H or even a constant V/H ratio is used in some codes to obtain a vertical response spectrum from corresponding horizontal spectrum (Zolfaghari and Darzi 2019b), and therefore, Chen et al. (2017) analyzed vertical-to-horizontal response spectral ratios for offshore ground motions by presenting the mean V/H ratios of nine earthquakes and proposed a simplified design equation for the V/H ratio of offshore ground motions, in which only the moment magnitude and the period-dependent variation are considered. However, the simplified equation proposed by Chen et al. (2017) does not consider the differences in V/H ratios between offshore stations due to varying local site geologies of offshore stations (Dhakal et al. 2017). As we found that the suggested V/H ratios by Chen et al. (2017) are lower for some offshore stations, we attempt to develop a more appropriate V/H model for offshore ground motions for the Sagami offshore region, and the proposed offshore V/H model is used to facilitate the assessment of response spectra of vertical components using V/H ratios when the horizontal component of the response spectrum is known.

In this article, a prediction model for V/H ratios for the offshore area off Sagami Bay in Japan is developed based on all available offshore records. We first analyze the correlation between offshore V/H ratios with the moment magnitude, hypocentral distance, focal depth, and tectonic source type by dividing the offshore dataset into different groups based on previous research methods on the V/H prediction model. To directly compare the differences in V/H ratios of the offshore and onshore ground motions of this region, the onshore V/H ratio prediction model is also proposed based on onshore records pertaining to the same set of earthquakes. To account for differences in local site conditions, individual site correction terms are used for the offshore sites in the offshore V/H model due to unavailable site condition data while site class terms are used for the onshore sites in the onshore model. The V/H ratios are defined as a function of the magnitude, hypocentral distance, focal depth, tectonic source type, and site conditions. The validity of the proposed models is examined by a detailed residual analysis, and the analysis shows that the offshore V/H model is not biased with regard to the moment magnitude, hypocentral distance, or focal depth. The results of direct comparisons show that the V/H ratios of offshore motions are significantly smaller than those of onshore motions for short moderate spectral periods (T < 1.0 s) and are comparable for periods longer than 1.0 s.

2 Strong ground motion database

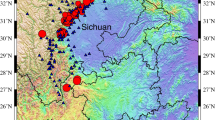
There are six offshore sites, namely KNG201, KNG202, KNG203, KNG204, KNG205, and KNG206, deployed below the seafloor off Sagami Bay. We examined these 6 offshore sites of the K-NET ETMC network in addition to 23 onshore stations from K-NET adjacent to the offshore area. Figure 1 shows the distributions of the offshore sites, onshore sites, and earthquakes used in this study. Filled circles indicate earthquake epicenters, the colors of the circles denote the focal depths of the earthquakes, red squares denote the 6 offshore sites, and black triangles denote the 23 onshore stations. The background color denotes the elevation of the land and seafloor with the deepest elevation denoted by the darkest color. The distances between two adjacent offshore sites range from 10 to 20 km, and the water depths of these offshore sites range from approximately 900 to 2300 m. Detailed information about the deployment of the offshore sites used in this study can be found in Eguchi et al. (1998). Table 1 presents detailed information corresponding to the offshore and onshore sites used in this study. All strong motion records from the offshore and onshore sites and corresponding soil condition data, including P-wave and S-wave logs and standard penetration test values, are available on the K-NET website (http://www.kyoshin.bosai.go.jp/, last accessed June 2019) (Aoi et al. 2004).

Fig. 1
figure 1

Geographic distribution map of earthquakes and strong ground motion recording stations around Sagami Bay in Japan. Triangles and squares denote the offshore and onshore stations in the Sagami Bay area, respectively, and circles, scaled by moment magnitude, denote the earthquake epicenters used in this study. The colors of the circles denote the focal depths of the earthquakes. Background colors denote elevations of the land and seafloor with the deepest elevation denoted by the darkest color

Full size image
Table 1 Information on the offshore sites and onshore stations used in this study
Full size table

All available events recorded by the six offshore stations from earthquakes occurring between 2000 and 2018 were examined in this study. We excluded some offshore records using the following criteria: records must include both P-wave and S-wave onsets, the signal-to-noise ratio (SNR) of the three components of the records should be greater than 3 for each component, the source-to-site distance (epicentral distance) must be less than 300 km, the focal depth must be shallower than 180 km, and the moment magnitude must not be smaller than 4.0. The dataset of offshore strong ground motions includes 738 three-component records from 233 events. In order to directly compare the differences of the V/H ratios between the offshore and onshore ground motions, onshore strong ground motions are also selected from the same set of earthquakes employed for the offshore dataset. Therefore, the dataset of onshore strong motions includes 2219 three-component onshore records from the same 233 events. Detailed information regarding the earthquake events used in this study can be found in Hu et al. (2020).

For the onshore stations studied here, we only have soil condition data for a depth range of 10–20 m, so the travel-time averaged shear-wave velocity to 30 m (VS30) is estimated using the extrapolation relations proposed by Boore et al. (2011). The estimated VS30 values for the onshore sites are listed in Table 1. Then, according to the estimated VS30 values, the onshore sites are categorized into four site classes, SC I, SC II, SC III, and SC IV, approximately corresponding to four classes of rock, hard soil, medium soil, and soft soil, respectively, as defined by Molas and Yamazaki (1995). Table 2 shows the site class definitions, and Table 1 shows the site codes of the onshore stations relating to the corresponding site classes.

Table 2 Site classification method used in the present study for onshore stations
Full size table

Japan is located above an active subduction zone, and many earthquakes occurring therein are associated with activity within and between the upper and lower tectonic plates. As the attenuation characteristics of different subduction-type earthquakes have been recognized (e.g., Youngs et al. 1997; Morikawa and Sasatani, 2004; Abrahamson et al. 2016), subduction earthquakes are typically classified as either subduction interface earthquakes or subduction slab earthquakes with respect to the tectonic source type. Therefore, the earthquake events used in this study are classified as crustal, interface, and slab events according to their locations (i.e., their epicentral locations and focal depths) with respect to the trench axis and their focal mechanisms. The results of the classification show that, in general, slab events are associated with normal-faulting events at focal depths of deeper than 50 km whereas interface events are associated with reverse-faulting events and are located between the coast and the trench axis at focal depths shallower than 50 km (Zhao et al. 2006; Montalva et al. 2017). In contrast, crustal events are characterized by either normal or strike-slip faulting mechanisms and focal depths shallower than 50 km. The focal mechanisms are differentiated based on a rake angle criterion (Boore et al. 1997). Rake angles within 30° of the horizontal are classified as strike-slip events while angles of 30 to 150° are regarded as reverse-faulting events, and angles of −30 to −150 are categorized as normal-faulting events. For a few events, the boundary values are adjusted based on the overall mechanism and tectonic environment involved. The epicentral coordinates and focal depths of the events are obtained from the Japan Meteorological Agency (JMA) while their moment magnitudes and focal mechanism solutions are obtained from the Full Range Seismograph Network of Japan (F-net) operated by the National Research Institute for Earth Science and Disaster Prevention (NIED). The source categories of the events can also be found in Hu et al. (2020).

Figure 2a and b show the distributions of the event magnitude and hypocentral distance for the earthquakes with focal depths reaching 180 km for the offshore and onshore strong motion datasets, respectively. The moment magnitudes of the events range from 4.0 to 6.8, and the hypocentral distances are less than 300 km. Within the offshore dataset, only a few records pertain to events occurring within a 30-km hypocentral distance, and no events were recorded within a 15-km hypocentral distance. Therefore, our offshore V/H model may not be appropriate for near-source earthquake prediction. Figure 2c and d show the distributions of the event magnitude and focal depth for the offshore and onshore datasets, respectively. The distributions of the offshore and onshore magnitudes and focal depths show reasonable levels of agreement. The offshore dataset includes 233 events, and the onshore dataset includes 223 events. Ten events are excluded from the onshore dataset because either the hypocentral distance exceeds 300 km or the SNRs of the records are smaller than 3.

Fig. 2
figure 2

Magnitude and distance or depth distributions of the offshore and onshore ground motions used in the present study

Full size image

Nearly all records obtained from the K-NET have baseline offsets and are contaminated with noise. Therefore, applying the processing method developed by Boore et al. (2002) and Boore and Bommer 2005, we use a simple scheme to process the records for each component as clearly stated in Hu et al. (2020). Numerical experiments show that the acceleration response spectra calculated from the accelerograms are not sensitive to the choice of the low-cut frequencies for oscillator periods of less than 0.5/fc, where fc = 0.05 Hz is suitable for computed spectral accelerations for periods of less than or equal to 10 s. The sampling rate of these records is either 50 Hz or 100 Hz, and thus, a high-cut frequency of 25 Hz is used to eliminate ground motions over 25 Hz. This high-cut frequency is determined by examining the Fourier spectra of all available records, thereby demonstrating that the main part of each record is retained in the selected frequency band.

3 Exploration of functional form

To understand the effect of these explanatory variables, i.e., the moment magnitude, hypocentral distance, focal depth, and tectonic source type, on the offshore V/H ratios, a preliminary analysis of these V/H ratios with respect to different magnitude, distance, depth, and source type groups are compared over varying periods. Figure 3 shows the observed trends in the offshore V/H ratios with respect to different groups. As shown in Fig. 3a, the offshore V/H ratios are divided into three groups by three magnitudes, i.e., magnitudes of less than 5.0, between 5.0 and 6.0, and larger than 6.0, and the mean offshore V/H ratios of each group are plotted as varying with periods with different line styles. Figure 3b–d show the varying trends of the offshore V/H ratios with periods for different hypocentral distance, focal depth, and tectonic source type groups, respectively. The mean offshore V/H ratio ordinates are comparable for periods of shorter than1.0 s for different magnitude, distance, depth, and source type groups, but as the period increases, the mean offshore V/H ratio changes for all groups. The mean offshore V/H ratio changes with the moment magnitude in periods lasting longer than 1.0 s. The larger the moment magnitude, the larger the offshore V/H ratios. Differences are also found between the mean offshore V/H ratio for PGA and spectral periods of less than 0.05 s. The varying trends for different hypocentral distance groups are not obvious for periods longer than 2.0 s with the main difference being that the mean V/H ratio of the group for distances longer than 160 km is significantly larger than those of the other two groups with short moderate hypocentral distances for periods lasting longer than 2.0 s. For the effect of focal depth, the mean V/H ratio of depths of deeper than 60 km is smaller for the other two groups for periods longer than 1.0 s and is similar to those for periods of less than 1.0 s. We can confirm that the deeper the focal depth, the smaller the offshore V/H ratio, mainly for long periods (> 1.0 s). The tectonic source type also affects the offshore V/H ratio mainly for long periods. Therefore, the moment magnitude, hypocentral distance, focal depth, and earthquake type have little effect on the offshore V/H ratio for periods ranging from 0.05 to 1.0 s; however, these explanatory variables apparently have an effect for periods of longer than 1.0 s and have moderate effects on offshore V/H ratios for periods of less than 0.05 s.

Fig. 3
figure 3

Preliminary analysis of offshore ground motion V/H ratios for different magnitude groups (a), hypocentral distance groups (b), focal depth groups (c), and earthquake type groups (d)

Full size image

To compare differences in the effects of these variables on V/H ratios of the offshore and onshore ground motions, the varying trends of the mean onshore V/H ratios for different groups are presented in Fig. 4. The differences in onshore V/H ratio across these groups are not large for the entire period band, and the overall effects of these explanatory variables on the mean onshore V/H ratios are not as clear as those shown in Fig. 3. The effect level of these variables on the onshore V/H ratio is similar to those presented for other onshore regions (Bommer et al. 2011; Zolfaghari and Darzi 2019a). The spectral shapes of the offshore and onshore V/H ratios are significantly different, and the effects of variables on the V/H ratios are also not consistent. To find the best functional form and to avoid overcomplicating the form of the offshore V/H model, varying trends of the offshore V/H ratio with magnitude, distance, depth, and source type are investigated in Fig. 3 and compared to the onshore V/H ratios given in Fig. 4. Therefore, these variables are considered in the V/H prediction model by using a simple functional form.

Fig. 4
figure 4

Varying trends of onshore V/H ratios for different magnitude (a), hypocentral distance (b), focal depth (c), and earthquake source type groups (d)

Full size image

The characteristics of the observed offshore ground motion are considerably different from those of the onshore motions, but as soil condition data for the offshore sites are unavailable, an analysis of the site effect by the VS30 cannot be applied to the offshore sites. Therefore, we refer to the individual site term method of Takahashi et al. (2004) for the six offshore sites. Although the processing method of individual site terms is not the best for analyzing the offshore V/H ratio in considering the site effect, the individual site terms here could not only reduce the total sigma of the model by our preliminary analysis but also show differences between the offshore sites due to the different local site geologies present (Dhakal et al. 2017). As for the onshore stations, they are classified into four classes according to the obtained VS30 of these onshore stations as shown in Table 1.

Chen et al. (2017) presented a simplified design equation of offshore ground motion using only 54 offshore recordings. In their analysis, the mean V/H ratio of the six offshore sites is used, but according to Dhakal et al. (2017), the site geologies of offshore sites are not uniform, and therefore, the mean V/H ratio of offshore sites introduces uncertainty for predicting the offshore V/H ratio, and the prediction equation should be derived from more than 54 recordings. Although all available offshore ground motion records are used to develop the offshore V/H model in this study, the offshore dataset cannot provide robust constraint due to limited offshore records as shown in Fig. 2a. Therefore, we collected all available offshore recordings for the offshore area off Sagami Bay and fully considered the effects of the explanatory variables on the offshore V/H ratio.

The response spectra of the vertical offshore motion are much lower than those of the horizontal offshore motion mainly due to the effect of water layer (Boore and Smith 1999; Chen et al. 2015, 2017; Diao et al. 2014). The behaviors of median V/H ratios as functions of independent variables are investigated in Fig. 3. While referring to the prediction V/H ratio model developed by Gülerce and Abrahamson (2011) based on the Pacific Earthquake Engineering Research-Next Generation Attenuation of Ground Motions (PEER NGA) dataset and the prediction model for V/H ratios for Europe and the Middle East developed by Bommer et al. (2011), we considered the effect of the moment magnitude, hypocentral distance, focal depth, and tectonic source type on the offshore V/H ratio in the base functional form presented in Eq. (1):

$$ \ln \left(V/H\right)={b}_1{M}_w+{b}_2{M}_w^2+\left({b}_3+{b}_4{M}_w\right)\ln \left(\sqrt{R^2}+{b}_5^2\right)+{b}_{6^h}+{b}_7{F}_{\mathrm{I}}+{b}_8{F}_{\mathrm{S}}+{S}_k+{\mathrm{S}\mathrm{C}}_p $$
(1)

in which V/H is either V/H PGA or the 5%-damped V/H spectral acceleration ratio at spectral period T, Mw is the moment magnitude, R is the hypocentral distance in kilometers, and h is the focal depth in kilometers. FI and FS are the dummy variables for the tectonic source type. FI = 1.0 for the interface events, and FI = 0 for all other types of events; FS is 1 for subduction slab events and is 0 for all other events. Sk is the individual site term for a given station applying to offshore stations only, and S1–S6 represent the individual site term corresponding to offshore sites KNG201–KNG206, respectively; SCp is the site class term for a given site class applying to onshore stations only, and SC1–SC4 represent SC I–SC IV site classes for the onshore sites, respectively. In many previous studies (Gülerce and Abrahamson 2011; Bommer et al. 2011; Soghrat and Ziyaeifar 2016; Zolfaghari and Darzi 2019a, 2019b), coefficient b5 is kept as 5 km. Although the model is not well constrained over a short distance, the associated variability in our models is found to be at least as low as that obtained in other studies. When h is deeper than 130 km, h is set as 130 km so that a constant factor is used for deeper events. The horizontal PGA and horizontal spectral acceleration are both defined as the geometric mean of the two horizontal components.

The coefficients b1–b6, individual site term Sk, and site class term SCp were determined by regression analysis for each period, and the regression results of the base model shown in Eq. (1) are analyzed, echoing overfitting results shown in Bommer et al. (2011) and Zolfaghari and Darzi (2019a). Therefore, coefficients b2 and b4 are set as 0 to obtain a more reasonable functional form. The preliminary analysis of the base model shows that the base model without b2 and b4 (b2 = b4 = 0) can fit the offshore V/H ratio model better than the base model with b2 or b4, mainly because the number of offshore recordings is so limited that the magnitude square term and magnitude related attenuation term were not well constrained.

4 Regression analysis

Regression analyses to estimate the offshore V/H ratios for PGA and 5%-damped spectral accelerations of up to 10.0 s are conducted for the base model without b2 and b4; in turn, the final prediction model for the offshore and onshore V/H ratios is presented in Eq. (2):

$$ \ln \left(V/H\right)={b}_1{M}_w+{b}_3\mathrm{l}n\left(\sqrt{R^2+{b}_5^2}\right)+{b}_6\left(h-{h}_c\right){\delta}_h+{b}_7{F}_{\mathrm{I}}+{b}_8{F}_{\mathrm{s}}+{S}_k+{\mathrm{SC}}_p $$
(2)

The random effect model proposed by Abrahamson and Youngs (1992) was used in the V/H model of offshore and onshore ground motions, respectively. The total variability of the models can be expressed as the between-event (representing the event-to-event component of the total variability) and within-event (representing the site-to-site component of variability, path effects, and all other sources of variability not explicitly modeled) variability, and in this study, the between-event and within-event errors are assumed to be period dependent but independent of magnitude. Therefore, the model’s total standard deviation can be calculated as

$$ {\sigma}_T+\sqrt{\sigma^2+{\tau}^2} $$
(3)

in which σ and τ are the within-event and between-event standard deviations, respectively.

The regression results of Eq. (2) on the offshore and onshore V/H spectral ratio are presented in Tables 3 and 4, respectively. The last three columns of Tables 3 and 4 list the within-event, between-event, and total standard deviations of the offshore and onshore V/H model, respectively. Figure 5 shows the variations in the between-event, within-event, and total standard deviations for the offshore and onshore V/H models with respect to the spectral periods. The largest total standard deviations for the offshore and onshore V/H models are approximately 0.45 at 7.0 s and 0.48 at 0.25 s, respectively. The between-event variability is a minor contributor to the total variability, as is generally found in empirical GMPEs (Strasser et al. 2009), and the between-event variability between the onshore and offshore models is similar. We can conclude from Fig. 5 that the level of total sigma found in this study is similar to those presented in the proposed V/H models (Gülerce and Abrahamson 2011; Bommer et al. 2011; Zolfaghari and Darzi 2019a).

Table 3 Regression coefficients of the offshore V/H model
Full size table
Table 4 Regression coefficients of the onshore V/H model for comparison
Full size table
Fig. 5
figure 5

Variations of standard deviations of the offshore and onshore V/H model

Full size image

The validity of the offshore and onshore V/H spectral ratio models was investigated by conventional residual analysis. Figures 6 and 7 show the between-event residuals against moment magnitude Mw and focal depth, respectively, for PGA and spectral periods of T = 0.05, 0.2, 0.5, 1.0, and 3.0 s. The red error bars shown in Figs. 6 and 7 indicate average residuals within predetermined magnitude bins and depth bins and their corresponding ± σ bounds. The distributions of between-event residuals are unbiased with respect to magnitude and focal depth, and only a slight bias is found for long periods and large magnitudes most likely due to the poor distribution of the data. Figure 8 shows the distribution of within-event residuals in terms of hypocentral distance for PGA and periods of T = 0.05, 0.2, 0.5, 1.0, and 3.0 s. The distribution of the within-event residuals is unbiased within a hypocentral distance range of 15–300 km. A residual analysis of the onshore V/H model was also conducted and shows that the overall performance of the onshore model was well constrained. Therefore, the results of our analysis suggest that the offshore V/H prediction model given in Eq. (2) can be used to predict offshore V/H spectral ratios that are reasonably unbiased within a magnitude range of 4.0–7.8, a hypocentral distance of 15–300 km, and focal depths of 0–180 km.

Fig. 6
figure 6

Between-event residual distribution against the moment magnitude of the offshore V/H model for PGA and five spectral periods (T = 0.05, 0.2, 0.5, 1.0, and 3.0 s)

Full size image
Fig. 7
figure 7

Between-event residual distribution against the focal depth of the offshore V/H model for PGA and five spectral periods (T = 0.05, 0.2, 0.5, 1.0, and 3.0 s)

Full size image
Fig. 8
figure 8

Within-event residual distribution against the hypocentral distance of the offshore V/H model for PGA and five spectral periods (T = 0.05, 0.2, 0.5, 1.0, and 3.0 s)

Full size image

5 Predicted V/H spectral ratios and comparison with the onshore V/H model

In this section, we first show how the magnitude, hypocentral distance, focal depth, and tectonic source type influence the offshore V/H spectral ratio according to the regression results. To investigate the differences between the offshore and onshore V/H ratios, the attenuation characteristics of the two models are compared with varying hypocentral distances and different moment magnitudes. Figure 9 shows the varying trends of the offshore and onshore V/H ratios of given periods (PGA and T = 0.05, 0.2, 0.5, 1.0, and 3.0 s) with the hypocentral distance by setting magnitudes of 4, 5, and 6, respectively, focal depth of 20 km, the tectonic source type of the crustal earthquake, an S4 individual site term for offshore sites, and an SC2 site class term for onshore sites. The offshore V/H ratios are denoted by black lines, and the onshore V/H ratios are denoted by red lines in Fig. 9. Although the effect of the hypocentral distance is observed and this effect is different in different periods, the influence of hypocentral distance is not obvious. Moment magnitude effects for the offshore V/H ratios are also observed for PGA, T = 0.05, and T = 3.0 s, which is consistent with trends observed in Fig. 3. The moment magnitude mainly affects the shortest periods (T < 0.05 s) and longer periods (T > 1.0 s), and the effect of the hypocentral distance is almost absent for short periods (T < 0.5 s), and for long periods (T > 0.5 s), a longer distance will always correspond with larger offshore V/H ratios. The direct comparison of offshore and onshore V/H ratios given in Fig. 9 shows that offshore V/H ratios are much lower than onshore V/H ratios for periods of less than 0.5 s, and for longer periods, obvious differences between them are not observed, which is mainly attributable to the water layer (Chen et al. 2015; Diao et al. 2014). As the number of offshore records is limited for constraining the offshore V/H model, the physical explanation of the effects of these explanatory variables need further investigation after accounting for the effects of the water depth and the sediment thickness in the future with more offshore records.

Fig. 9
figure 9

Varying trend of the offshore and onshore V/H ratio of given periods (PGA and T = 0.05, 0.2, 0.5, 1.0, and 3.0 s) with the hypocentral distance by setting the magnitudes of 4, 5, and 6, respectively, focal depth of 20 km, the tectonic source type of the crustal earthquake, an S4 individual site term for offshore sites, and an SC2 site class term for onshore sites

Full size image

Figure 10 shows the effects of the tectonic source type and focal depth on the V/H ratios predicted from the offshore model. The basic model given in Eq. (2), i.e., where the source type and depth terms are both zero, is intended for crustal events with a focal depth of 15 km or less. Figure 10a shows that for periods of less than 0.1 s, the offshore V/H ratios show almost no differences with considering tectonic source types, i.e., crustal, interface, and slab earthquake events; beyond 0.1 s, offshore V/H ratios with interface events are smaller than those of the basic model with crustal events and represent approximately 80% of the offshore V/H ratios drawn from the basic model for periods of longer than 3.0 s. For slab events, the largest difference found between the basic model and the model with slab events is valued at roughly 10%; therefore, the slab events do not seem to have a strong influence on the offshore V/H ratios. Figure 10b shows the effects of the focal depth on the proposed offshore V/H model. The offshore V/H ratio for the deeper depth is larger than that for the shallower depth for spectral periods of shorter than 0.5 s and is smaller than that of the shallower depth for periods of longer than 0.5 s. Therefore, the effect of the focal depth is significant for the offshore V/H model, but the effect of the tectonic source type seems to be insignificant for periods of less than 5.0 s.

Fig. 10
figure 10

Scale factors for the a source types with respect to crustal events for the offshore V/H model and b focal depth with respect to events with a focal depth of h = 15 km or less for the offshore V/H model

Full size image

Figure 11 shows the variations in the predicted median V/H response spectral ratios of the offshore and onshore ground motions for specific magnitude and distance combinations for a crustal event with a focal depth of 20 km, using the S1 individual site term for offshore sites and the SC2 site class term for onshore sites. The hypocentral distance seems to have little effect on the offshore and onshore V/H ratios, but the magnitude significantly affects the offshore V/H ratio for periods shorter than 0.05 s and longer than 1.0 s. Most of the offshore V/H ratios are smaller than the onshore V/H ratios for spectral periods of less than 1.0 s; then, the offshore V/H ratios increase gradually to be comparable or even larger than the onshore V/H ratio for periods of 1.0 to 3.0 s, and for periods longer than 3.0 s, the offshore V/H ratios are slightly smaller than the onshore V/H ratio, which is consistent with the preliminary analysis given in Figs. 3 and 4. The overall reduction found for short moderate periods (T < 1.0 s) is mainly attributable to water layer and the deep deposition layer covering on the seafloor (Otsuka 1985; Chen et al. 2015; Hu et al. 2020). As Hu et al. (2020) stated in their study, both horizontal and vertical offshore response spectra are significantly larger than onshore response spectra, except that vertical response spectra for short moderate periods (T < 1.0 s) are slightly smaller than those of onshore motions. The observed amplification in offshore ground motions and the large variability in offshore site responses show site-specific studies are needed for offshore structures (Hu et al. 2020). Hence, the offshore V/H model can facilitate the construction of the vertical response spectrum in PSHA and can be used in seismic analysis for the combined input of vertical and horizontal ground motions.

Fig. 11
figure 11

Variations in the predicted median V/H response spectral ratio of the offshore and onshore ground motions for specific magnitude and distance combinations for a crustal event with a focal depth of 20 km, using S1 individual site term for offshore sites and SC2 site class term for onshore sites

Full size image

As local site geologies between the offshore sites are not uniform (Dhakal et al. 2017), we compared differences in offshore V/H ratios among the offshore sites as shown in Fig. 12. The individual site term S1 was used for comparisons in Fig. 11, but differences between the offshore sites are not considered in Fig. 11. Most of the offshore sites (KNG201, KNG203, KNG205, and KNG206) have a similar spectral shape, and the offshore V/H ratios observed in the four offshore sites are much smaller than the onshore V/H ratios for periods of less than 1.0 s and are comparable for longer periods. However, the offshore V/H ratios of KNG202 and KNG204 are apparently larger than those of the other four offshore sites and are comparable or even larger than the onshore V/H ratios for short and moderate periods. The large variability of V/H ratios in the offshore sites shows that the mean offshore V/H ratio of the offshore sites results in significant levels of uncertainty, and therefore, the site-specific studies for offshore V/H ratios are needed. The offshore V/H ratios are much different between offshore sites even with similar water depth, e.g., KNG201 and KNG202 from Fig. 12a, b. Therefore, the effect of water depth is unclear from this study and needs further investigation in the future by accounting for the water depth and the sediment thickness under offshore sites.

Fig. 12
figure 12

Comparison between the predicted offshore and onshore V/H ratio for different offshore sites and onshore class with SC2 site class

Full size image

Therefore, the prediction model used in this study considers the effect of moment magnitudes, hypocentral distances, focal depths, tectonic source types, and site differences. Among these explanatory variables, the individual site term mainly affects the spectral shape of the offshore V/H ratio, and the magnitude has a significant influence on the offshore V/H ratio while the effects of the hypocentral distance and tectonic source type are not as obvious as the effect of the magnitude. Given the large differences observed in offshore and onshore V/H ratios, the combination of vertical and horizontal ground motions for seismic analysis does not need to follow the recommendation to use a V/H ratio of 0.5 for the seismic analysis of an offshore platform.

6 Summary and conclusions

A prediction model for vertical-to-horizontal (V/H) response spectral ratios of offshore ground motions for the offshore area off Sagami Bay accounting for tectonic source types and focal depths was developed in this study. The onshore V/H model derived from an onshore dataset is also presented for comparisons. The prediction errors of our offshore V/H models are at least as low as those reported in other studies. The conventional residual analysis shows that our offshore V/H model is not biased with regard to magnitude, hypocentral distance, or focal depth. In the present model, predictions made in a near-source offshore region are not as reliable as predictions made on the moderate or far fields, as the offshore strong motion dataset does not include near-source records for hypocentral distances of 1–15 km. The magnitude range of the data for offshore models is 4.0–6.8, and the hypocentral distance range is 15–300 km.

As local site geologies of offshore sites are not uniform and as corresponding site condition data are unavailable, individual site terms were used for offshore sites in the offshore V/H model while site class terms were used for onshore sites in the onshore model. The regression results show that the hypocentral distance and tectonic source type have little influence on the offshore V/H ratios, but the magnitude and focal depth have a significant influence on the offshore V/H ratios. A direct comparison of offshore and onshore V/H ratios shows that the offshore V/H ratios are much smaller than the onshore V/H ratios for periods of less than 1.0 s and are comparable or even larger for periods of longer than 1.0 s. The deep deposition soil layer may amplify both horizontal and vertical ground motions. However, the water layer may reduce the amplitude of vertical motions, and this reduction decreases as periods increase.

Both horizontal and vertical offshore response spectra are significantly larger than onshore response spectra except that vertical response spectra for short moderate periods (T < 1.0 s) are slightly smaller than those of onshore motions (Hu et al. 2020). Therefore, the observed reduction in the offshore V/H ratios may also reflect the combined effect of water layer and the deep deposition layer. Due to the observed amplification in offshore motions across the entire period band (Hu et al., 2020), the common practice of selecting onshore records for the seismic design of offshore structures is inappropriate. Hence, the offshore V/H model can facilitate the construction of the vertical response spectrum in PSHA and can be used in seismic analysis for the combined input of vertical and horizontal ground motions.