Frequency dependence of long-period t*

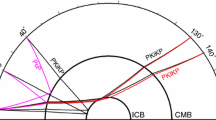
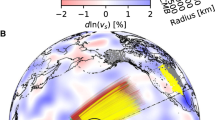
Abstract

Multi-phase long-period t* measurements are among the key evidences for the frequency-dependent mantle attenuation factor, Q. However, similarly to Q, poorly constrained variations of Earth’s structure may cause spurious frequency-dependent effects in the observed t*. By using an attenuation-coefficient approach which incorporates measurements of geometric spreading (GS), such effects can be isolated and removed. The results show that the well-known increase of body P-wave t* from ~0.2 s at short periods to ~1–2 s at long periods may be caused by a small and positive bias in the underlying GS, which is measured by a dimensionless parameter γ* ≈ 0.06. Similarly to the nearly constant t* at teleseismic distances, this GS bias is practically range-independent and interpreted as caused by velocity heterogeneity within the crust and uppermost mantle. This bias is accumulated within a relatively thin upper part of the lithosphere and may be closely related to the crustal body-wave GS parameter γ ~ 4–60 mHz reported earlier. After a correction for γ, P-wave t _P * becomes equal ~0.18 s at all frequencies. By using conventional dispersion relations, this value also accounts for ~40 % of the dispersion-related delay in long-period travel times. For inner-core attenuation, the attenuation coefficient shows a distinctly different increase with frequency, which is remarkably similar to that of fluid-saturated porous rock. As a general conclusion, after the GS is accounted for, no absorption-band type or frequency-dependent upper-mantle Q is required for explaining the available t* and velocity dispersion observations. The meaning of this Q is also clarified as the frequency-dependent part of the attenuation coefficient. At the same time, physically justified theories of elastic-wave attenuation within the Earth are still needed. These conclusions agree with recent re-interpretations of several surface, body and coda-wave attenuation datasets within a broad range of frequencies.

Appendix: Phase-velocity dispersion

Body-wave dispersion relations are often derived from Kramers–Krönig {XE “Kramers–Krönig”} integrals and relate the frequency dependence of phase velocity to Q. In this appendix, we show that the meaning of this Q corresponds to the “effective” Q _e given in Eq. (3).

Following Aki and Richards (2002, pp. 167–169), consider a harmonic wave of frequency ω, travelling in a uniform medium with phase velocity V(ω) = ω/k, with spectral amplitude u(ω) = exp(–iωx/V _∞ + ikx − αx), where k(ω) is the wavenumber, α(ω) is the attenuation coefficient and V _∞ = V(ω)| _{ω → ∞}. This expression describes a harmonic wave with an infinite-frequency onset at point x occurring at time t = 0. To ensure that also u (t) ≡ 0 for all t < 0 (causality), the Kramers–Krönig {XE “Kramers–Krönig”} identities require that the imaginary part of the wavenumber (α) is uniquely related to its real part (k) and vice versa. If we consider limits of α ₀ = α(0) and V _∞ to be finite, then k(ω) turns out to be insensitive to α ₀ and α(ω) is insensitive to V _∞, and the Kramers–Krönig integrals relate the deviations of k′ = k − ω/V _∞ and α′ = α − α ₀ from these reference levels (ibid):

$$ \left\{ {\matrix{ {k'\left( \omega \right) = \frac{\omega }{\pi }P\int_{{ - \infty }}^{\infty } {{\text d} \omega '} \frac{{\alpha '\left( {\omega '} \right)}}{{\omega ' - \omega }},} \\ {\alpha '\left( \omega \right) = - \frac{\omega }{\pi }P\int_{{ - \infty }}^{\infty } {{\text d} \omega '} \frac{{k'\left( {\omega '} \right)}}{{\omega '\left( {\omega ' - \omega } \right)}}.} \\ }<!end array> } \right. $$

(18)

Parameters V _∞ and α ₀ can also be viewed as regularization constants for the integrals in Eq. (18), which are otherwise divergent (Nussenzveig 1972).

Causality relations show that if some wave experiences attenuation (α > 0), it must also exhibit phase-velocity dispersion and vice versa. In principle, these equations allow expressing the phase-velocity spectrum if attenuation is known at all frequencies. However, these integrals converge very slowly near ω′ → ∞ and ω′ → ω, and therefore, much of the information required for using these expressions to predict either k(ω) or α(ω) lies in the regions of unphysically high or low frequencies.

The case of α proportional to ω is of particular interest because there exists good evidence for it in both observations (Morozov 2008, 2010a, b) and theory (Morozov 2010d). However, in this case, the integral in the first equation in Eq. (18) is divergent and needs to be regularized. Such regularization can be done, for example, by assuming that α ≈ α ₀ + α ₁ ω within the seismic frequency band but flattens out at some high frequencies |ω| ≫ ω ₀ (modified after Azimi et al. 1968),

$$ \alpha \left( \omega \right) = {\alpha_0} + \frac{{{\alpha_1}\omega }}{{1 + \frac{\omega }{{{\omega_0}}} }}. $$

(19)

From Eq. (18), the corresponding phase slowness is only sensitive to α ₁ and ω ₀:

$$ \frac{1}{{V\left( \omega \right)}} - \frac{1}{{{V_{\infty }}}} = C - \frac{{2{\alpha_1}}}{{\pi \left[ {1 - {{\left( { \frac{\omega }{{{\omega_0}}} } \right)}^2}} \right]}}\ln \left( {\frac{\omega }{{{\omega_0}}}} \right) \approx C - \frac{{2{\alpha_1}}}{\pi }\ln \left( {\frac{\omega }{{{\omega_0}}}} \right), $$

(20)

where C is yet another regularization constant which is formally equal infinity in order to satisfy a finite value of $\mathop{{\lim }}\limits_{{\omega \to \infty }} V\left( \omega \right) = {V_{\infty }}$. We can remove this constant by switching the reference velocity from V _∞ to V ₀ = V(ω ₀):

$$ \frac{1}{{V\left( \omega \right)}} - \frac{1}{{{V_0}}} \approx - \frac{{2{\alpha_1}}}{\pi }\ln \left( {\frac{\omega }{{{\omega_0}}}} \right). $$

(21)

Denoting, in accordance with our definition of Q _e, 2α ₁ = Q ⁻¹_e /V ₀, the velocity dispersion law becomes:

$$ V\left( \omega \right) \approx \frac{{{V_0}}}{{1 - \frac{1}{{\pi {Q_{\text{e}}}}}\ln \left( {\frac{\omega }{{{\omega_0}}}} \right)}}. $$

(22)

Equation (22) shows the general logarithmic phase-velocity increase with frequency in the presence of attenuation, which is supported by many attenuation models (e.g. Carcione {XE “Carcione, J.M.”} 2007). Parameters ω ₀ and V ₀ in Eq. (22) represent arbitrary constants on which the resulting values of phase velocities may depend very strongly. However, for Q and ω ₀ satisfying πQ _e ≫ |ln(ω/ω ₀)| and consequently V ≈ V ₀ within the observation frequency band, the ratios of V(ω) taken at frequencies ω ₁ and ω ₂ no longer depend on these regularization parameters (Aki {XE “Aki, K.”} and Richards {XE “Richards, P.G.”} 2002, p. 170):

$$ \frac{{V\left( {{\omega_1}} \right)}}{{V\left( {{\omega_2}} \right)}} \approx 1 + \frac{1}{{\pi {Q_{\text{e}}}}}\ln \left( {\frac{{{\omega_1}}}{{{\omega_2}}}} \right). $$

(23)

This ratio is often transformed into the “physical dispersion” relation and attributed to the viscoelastic moduli (Dahlen and Tromp 1998; p. 218), for example:

$$ \frac{{\mu \left( {{\omega_1}} \right)}}{{\mu \left( {{\omega_2}} \right)}} \approx 1 + \frac{2}{{\pi {Q_{\mu }}}}\ln \left( {\frac{{{\omega_1}}}{{{\omega_2}}}} \right). $$

(24)

The above equations can also be expressed as variations of V and μ with frequency:

$$ \delta \left( {\ln V} \right) \approx \frac{1}{{\pi Q}}\delta \left( {\ln \omega } \right){\text{ and}}\;\delta \left( {\ln \mu } \right) \approx \frac{2}{{\pi {Q_{\mu }}}}\delta \left( {\ln \omega } \right). $$

(25)

In order to understand the meaning of Q in dispersion laws (25), it is useful to try adding another “relaxation mechanism” with a different ω ₀ to Eq. (19):

$$ \alpha \left( \omega \right) = {\alpha_0} + \frac{{{\alpha_1}\omega }}{{1 + \frac{\omega }{{{\omega_{{0,1}}}}} }} + \frac{{{\alpha_2}\omega }}{{1 + \frac{\omega }{{{\omega_{{0,2}}}}} }}. $$

(26)

By combining such terms, practically any monotonic α(ω) functions increasing not faster than ω can be constructed. It is easy to verify that subject to the same approximation V ≈ V ₀, expression (23) becomes:

$$ \frac{{V\left( {{\omega_1}} \right)}}{{V\left( {{\omega_2}} \right)}} \approx 1 + \frac{1}{\pi }\left( {\frac{1}{{{Q_{{{\text{e}},1}}}}} + \frac{1}{{{Q_{{{\text{e}},2}}}}}} \right)\ln \left( {\frac{{{\omega_1}}}{{{\omega_2}}}} \right). $$

(27)

where 1/Q _e,1,2 = 2V _∞ α _1,2. This shows that velocity dispersion is sensitive to the derivative dα/dω = α ₁ + α ₂ near ω = 0 rather than to the cutoff frequency ω ₀. Therefore, the Q factor in expressions (22) and (23) should correspond to the derivative dχ/dω evaluated after the zero-frequency limit of χ is removed, which corresponds to our Q _e value (Eq. (3)). This is reflected in our notation in Eqs. (22) and (23).

In summary, causality constraints require velocity dispersion in the presence of attenuation, and yet the exact form of this dispersion should be determined from the specific wave models. Normally, any mechanical system possessing a time-domain (Lagrangian) description should behave causally. Similarly, Kramers–Krőnig integrals require a frequency-dependent attenuation α(ω) at least at the very high and very low frequencies. However, for practical purposes, this requirement is not very useful because the low-frequency cutoff below which Q ⁻¹ must decrease is about 10⁻⁹⁹ Hz for Q ≥ 30 (Futterman 1962). Thus, the causality principle only weakly constrains the properties of the medium and does not constrain any definite frequency dependence of V or Q within the seismological frequency band.