Skip to main content
SpringerLink
Log in

Stochastic ground-motion simulation of two Himalayan earthquakes: seismic hazard assessment perspective

  • Original article
  • Published:
Journal of Seismology Aims and scope Submit manuscript

An Erratum to this article was published on 23 November 2011

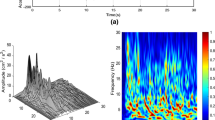
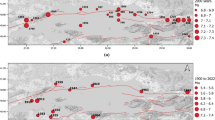
Abstract

The earthquakes in Uttarkashi (October 20, 1991, M w 6.8) and Chamoli (March 8, 1999, M w 6.4) are among the recent well-documented earthquakes that occurred in the Garhwal region of India and that caused extensive damage as well as loss of life. Using strong-motion data of these two earthquakes, we estimate their source, path, and site parameters. The quality factor (Q β ) as a function of frequency is derived as Q β (f) = 140f 1.018. The site amplification functions are evaluated using the horizontal-to-vertical spectral ratio technique. The ground motions of the Uttarkashi and Chamoli earthquakes are simulated using the stochastic method of Boore (Bull Seismol Soc Am 73:1865–1894, 1983). The estimated source, path, and site parameters are used as input for the simulation. The simulated time histories are generated for a few stations and compared with the observed data. The simulated response spectra at 5% damping are in fair agreement with the observed response spectra for most of the stations over a wide range of frequencies. Residual trends closely match the observed and simulated response spectra. The synthetic data are in rough agreement with the ground-motion attenuation equation available for the Himalayas (Sharma, Bull Seismol Soc Am 98:1063–1069, 1998).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  • Aki K (1980) Attenuation of shear waves in the lithosphere of frequencies from 0.05 to 25 Hz. Phys Earth Planet Interiors 21:50–60

    Article  Google Scholar 

  • Atkinson GM (1984) Attenuation of strong ground motion in Canada from a random vibration approach. Bull Seismol Soc Am 74:2629–2653

    Google Scholar 

  • Atkinson GM (2004) Empirical attenuation of ground-motion spectral amplitudes in southeastern Canada and the northeastern United States. Bull Seismol Soc Am 94:1079–1095

    Article  Google Scholar 

  • Atkinson GM, Boore DM (1995) Ground motion relations for eastern North America. Bull Seismol Soc Am 85:17–30

    Google Scholar 

  • Atkinson GM, Boore DM (2006) Earthquake ground-motion prediction equations for eastern North America. Bull Seismol Soc Am 96:2181–2205

    Article  Google Scholar 

  • Atkinson GM, Cassidy J (2000) Integrated use of seismograph and strong motion data to determine soil amplification in the Fraser delta: results from Duvall and Georgia state earthquakes. Bull Seismol Soc Am 90:1028–1040

    Article  Google Scholar 

  • Beresnev IA, Atkinson GM (2002) Source parameters of earthquakes in eastern and western North America based on finite-fault modeling. Bull Seismol Soc Am 92:695–771

    Article  Google Scholar 

  • Boore DM (1983) Stochastic simulation of high-frequency ground motions based on seismological models of the radiated spectra. Bull Seismol Soc Am 73:1865–1894

    Google Scholar 

  • Boore DM (1986) The effect of finite bandwidth on seismic scaling relationships. In: Das S, Boatwright J, Scholz C (eds) Earthquake source mechanics, geophysical monograph 37. American Geophysical Union, Washington DC, pp 275–283

    Chapter  Google Scholar 

  • Brune JN (1970) Tectonic stress and the spectra of seismic shear waves from earthquakes. J Geophys Res 75(26):4997–5009

    Article  Google Scholar 

  • Brune JN (1971) Corrections. J Geophys Res 76(26):6488

    Article  Google Scholar 

  • Chandrasekaran AR, Das JD (1992) Analysis of strong motion accelerogram of Uttarkashi earthquake of October 20, 1991. Bull Indian Soc of Earthq Tech 29(1):35–55

    Google Scholar 

  • Dewey JF, Bird JM (1970) Mountain belts and new global tectonics. J Geophys Res 75:2625–2647

    Article  Google Scholar 

  • Frankel A (1995) Simulating strong motions of large earthquakes using recordings of small earthquakes—the Loma Prieta main-shock as a test case. Bull Seismol Soc Am 85:1144–1160

    Google Scholar 

  • Gupta SC, Kumar A (2002) Seismic wave attenuation characteristics of three Indian regions: a comparative study. Curr Sci 82:407–413

    Google Scholar 

  • Gupta SC, Teotia SS, Rai SS, Gautam N (1998) Coda Q estimates in the Koyna region, India. Pure and Appl Geophys 153:713–731

    Article  Google Scholar 

  • Gupta SC, Singh VN, Kumar A (1995) Attenuation of coda waves in the Garhwal Himalaya, India. Phys of Earth and Planet Interiors 87(3):247–253

    Article  Google Scholar 

  • Hanks TC, McGuire RK (1981) The character of high frequency strong ground motion. Bull Seismol Soc Am 71:2071–2095

    Google Scholar 

  • Hermann RB (1985) An extension of random vibration theory estimated of strong ground motion to large distances. Bull Seismol Soc Am 75:1447–1553

    Google Scholar 

  • Huang CH, Teng TL (1999) An evaluation of H/V ratio vs. spectral ratio for the site-response estimation using the 1994 Northridge earthquake sequences. Pure and App Geophys 156:631–649

    Article  Google Scholar 

  • Joshi A (2004) A simplified technique for simulating wide-band strong ground motion for two recent earthquakes. Pure and App Geophys 161:1777–1805

    Article  Google Scholar 

  • Joshi A (2006) Use of acceleration spectra for determining the frequency dependent attenuation coefficient and source parameter. Bull Seismol Soc Am 96:2165–2180

    Article  Google Scholar 

  • Khattri KN, Chander R, Gaur VK, Sarkar I, Kumar S (1989) New seismological results on the tectonics of the Garhwal Himalaya. Proc Indian Acad Earth Planet Sci 98:91–109

    Google Scholar 

  • Kumar N, Parvez IA, Virk HS (2004) Estimation of coda waves attenuation for NW Himalayan region using local earthquakes, research report CM-0404, C MMACS, India

  • Kumar D, Sarkar I, Sriram V, Khattri KN (2005) Estimation of the source parameters of the Himalaya earthquake of October 19, 1991, average effective shear wave attenuation parameter and local site effects from accelerogram. Tectonophysics 407:1–24

    Article  Google Scholar 

  • Langston CA, Chi Chiu SC, Lawrence Z (2010) Array observations of micro-seismic noise and the nature of H/V in the Mississippi embayment. Bull Seismol Soc Am 99(5):2893–2911

    Article  Google Scholar 

  • Le fort P (1975) Himalaya, the collided range. Am J Sci 278:1–44

    Google Scholar 

  • Lermo L, Chavez-Garcia FJ (1993) Site effect evaluation using spectral ratio with only one station. Bull Seismol Soc Am 83:1574–1594

    Google Scholar 

  • Mandal P, Rastogi BK (1998) A frequency-dependent relation of coda Qc for Koyna Warna region, India. Pure Appl Geophys 153:163–177

    Article  Google Scholar 

  • Molnar P, Tapponnier P (1975) Cenozoic tectonics of Asia: effect of continental collision. Science 489:419–426

    Article  Google Scholar 

  • Motazedian D, Atkinson GM (2005) Stochastic finite-fault modeling based on dynamic corner frequency. Bull Seismol Soc Am 95(3):995–1010

    Article  Google Scholar 

  • Motazedian D (2006) Region specific key seismic parameters of earthquakes in northern Iran. Bull Seismol Soc Am 96:1383–1395

    Article  Google Scholar 

  • Nakamura Y (1989) A method of dynamic characteristics estimation of subsurface using micro-tremor on the ground surface. Quarterly Report on Railroad Research 30:25–33

    Google Scholar 

  • Narula PL (1992) Neo-tectonic activity, seismicity and related contemporary deformation in the NW Himalaya. Intl Symp on Himalayan Geology, Shimate, Japan, pp 33–36

  • Paul A, Gupta SC, Pant CC (2003) Coda Q estimate from Kumaon Himalaya. Proc Ind Acad Soc Earth Planet Sc 112:569–678

    Google Scholar 

  • Schnabel PB, Lysmer J, Seed HB (1972) A computer program of earthquake response analysis of horizontally layered sites. Report no. EERC72-12, University of California, Berkeley

  • Sharma ML (1998) Attenuation relationship for estimation of peak ground horizontal acceleration using data from strong motion arrays in India. Bull Seismol Soc Am 98:1063–1069

    Google Scholar 

  • Seeber L, Armbruster JG (1981) Great detachment earthquakes along the Himalayan arc and long term earthquake prediction: an international review. American Geophysical Union, Washington, DC, pp 259–277

    Google Scholar 

  • Silva W, Gregor N, Darragh R (2002) Department of Regional Hard Rock Attenuation Relations for Central and Eastern North America. ftp://ftp.pacificengineering.org/CEUS/

  • Singh SK, Ordaz M, Dattatrayam RS, Gupta HK (1999) A spectra analysis of the 21 May 1997, Jabalpur, India earthquake (Mw 5.8) and estimation of ground motion from future earthquakes in the Indian shield region. Bull Seismol Soc Am 89(6):1620–1630

    Google Scholar 

  • Singh SK, Garcia D, Pacheo JF, Valenzuela R, Bansal BK, Dattatrayam RS (2004) Q of Indian shield. Bull Seismol Soc Am 94:1564–1570

    Article  Google Scholar 

  • Suzuki T, Adachi Y, Tanaka M (1995) Application of micro tremor measurement to the estimation of earthquake ground motion in Kushiro City during the Kushiro-Oki earthquake of 15 January 1993. Earthq Eng Struct Dyn 24:595–613

    Article  Google Scholar 

  • Thakur VC (1993) Geology of Western Himalaya. Pergman, Oxford, p 355

    Google Scholar 

  • Thakur VC, Kumar S (1995) Seismotectonics of the 20 October 1991 Uttarkashi earthquake in Garhwal Himalaya, North India. Memoir Geol Soc of India 30:101–108

    Google Scholar 

  • Theodulis NP, Bard PY (1995) Horizontal to vertical spectral ratio and geological conditions: an analysis of strong motion data from Greece and Taiwan (SMART-1). Soil Dyn Earthq Eng 14:177–197

    Article  Google Scholar 

  • Toro GR, McGuire RK (1987) An investigation into earthquake ground motion characteristics in the eastern North America. Bull Seismol Soc Am 77:468–489

    Google Scholar 

  • Valdiya KS (1988) Tectonics and evolution of the central sector of the Himalaya. Phil Trans Roy Soc London A 326:801–803

    Google Scholar 

  • Vladimir Yu, Sokolov Chin-Hsiung Loh, Jean Wen-Yu (2007) Application of horizontal to-vertical (H/V) Fourier spectral ratio for analysis of site effect on rock (NEHRP-class B) sites in Taiwan. Soil Dyn and Earthq Eng 27(4):314–323

    Article  Google Scholar 

  • Yu G, Khattri KN, Anderson JG, Brune JN, Zeng Y (1995) Strong ground motion from the Uttarkashi, Himalaya, India Earthquake: comparison of observation with synthetics using the composite source model. Bull Seismol Soc Am 85:31–50

    Google Scholar 

Download references

Acknowledgments

Thanks are due to anonymous reviewers for their constructive comments and suggestions for improving the article. We are also thankful to the Department of Earthquake Engineering, IIT Roorkee and the Indian Meteorological Department for providing Earthquake data. The support of the Centre of Excellence in Disaster Mitigation & Management, IIT Roorkee is gratefully acknowledged.

Author information

Authors and Affiliations

  1. Department of Earthquake Engineering, Indian Institute of Technology, Roorkee, India

    Ashish Harbindu & Mukat Lal Sharma

  2. Department of Earth Sciences, Indian Institute of Technology, Roorkee, India

    Kamal

Authors
  1. Ashish Harbindu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mukat Lal Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kamal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mukat Lal Sharma.

Additional information

An erratum to this article can be found at http://dx.doi.org/10.1007/s10950-011-9259-2.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Harbindu, A., Sharma, M.L. & Kamal Stochastic ground-motion simulation of two Himalayan earthquakes: seismic hazard assessment perspective. J Seismol 16, 345–369 (2012). https://doi.org/10.1007/s10950-011-9247-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10950-011-9247-6

Keywords

Search

Navigation