Crystal Growth and Magneto-transport of Bi₂Se₃ Single Crystals

Abstract

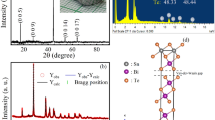
In this letter, we report on the growth and characterization of bulk Bi ₂Se ₃ single crystals. The studied Bi ₂Se ₃ crystals are grown by the self-flux method through the solid-state reaction from high-temperature (950 °C) melt of constituent elements and slow cooling (2 ℃/h). The resultant crystals are shiny and grown in the [00l] direction, as evidenced from surface XRD. Detailed Reitveld analysis of powder X-ray diffraction (PXRD) of the crystals showed that these are crystallized in the rhombohedral crystal structure with a space group of R3m (D5), and the lattice parameters are a = 4.14 (2), b = 4.14 (2), and c = 28.7010 (7) Å. Temperature versus resistivity (ρ−T) plots revealed metallic conduction down to 2 K, with typical room temperature resistivity (ρ _{300 K}) of around 0.53 m Ω-cm and residual resistivity (ρ _{0 K}) of 0.12 m Ω-cm. Resistivity under magnetic field [ ρ(T)H] measurements exhibited large + ve magneto-resistance right from 2 to 200 K. Isothermal magneto-resistance [ ρH] measurements at 2, 100, and 200 K exhibited magneto-resistance (MR) of up to 240 %, 130 %, and 60 %, respectively, at 14 T. Further, the MR plots are nonsaturating and linear with the field at all temperatures. At 2 K, the MR plots showed clear quantum oscillations at above say 10 T applied field. Also, the Kohler plots, i.e., Δρ/ ρ _oversus B/ ρ, were seen consolidating on one plot. Interestingly, the studied Bi ₂Se ₃ single crystal exhibited the Shubnikov-de Haas (SdH) oscillations at 2 K under different applied magnetic fields ranging from 4 to 14 T.