DFT study of the geometrical and electronic structure of substituted cumulenes in netral and cationic forms

Abstract

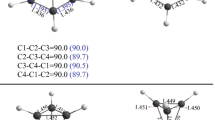
The geometrical and basic energy parameters of monosubstituted cumulenes and their singly and doubly charged cations were calculated by the Hartree-Fock and density functional (DFT) methods at a B3LYP level of theory using the 6-31G(d) basis set. The substituent was fluorine, cyan, amino group, phenyl, cyanophenyl, aminophenyl, or dimethylaminophenyl. In extended linear carbon systems based on cumulene, rotation of a terminal fragment depends on the character of the highest occupied molecular orbital (HOMO) from which electrons are removed. The terminal group rotates through 90 only when the contribution of electron density from the π molecular orbital (MO) of unsubstituted cumulene to the HOMO of substituted cumulene is over 70%. Otherwise, the terminal group rotates through a smaller angle; with a contribution of less than 30%, the dication is planar in any substituted cumulene. Thus quantitative criteria have been determined to evaluate the specific structural effect due to ionization of substituted cumulenes.