MPBPK-TMDD models for mAbs: alternative models, comparison, and identifiability issues

Abstract

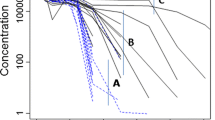
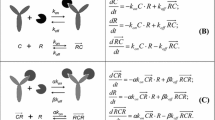
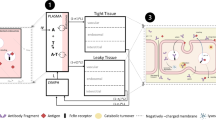
The aim of the present study was to evaluate model identifiability when minimal physiologically-based pharmacokinetic (mPBPK) models are integrated with target mediated drug disposition (TMDD) models in the tissue compartment. Three quasi-steady-state (QSS) approximations of TMDD dynamics were explored: on (a) antibody-target complex, (b) free target, and (c) free antibody concentrations in tissue. The effects of the QSS approximations were assessed via simulations, taking as reference the mPBPK-TMDD model with no simplifications. Approximation (a) did not affect model-derived concentrations, while with the inclusion of approximation (b) or (c), target concentration profiles alone, or both drug and target concentration profiles respectively deviated from the reference model profiles. A local sensitivity analysis was performed, highlighting the potential importance of sampling in the terminal pharmacokinetic phase and of collecting target concentration data. The a priori and a posteriori identifiability of the mPBPK-TMDD models were investigated under different experimental scenarios and designs. The reference model and QSS approximation (a) on antibody-target complex were both found to be a priori identifiable in all scenarios, while under the further inclusion of QSS approximation (b) target concentration data were needed for a priori identifiability to be preserved. The property could not be assessed for the model including all three QSS approximations. A posteriori identifiability issues were detected for all models, although improvement was observed when appropriate sampling and dose range were selected. In conclusion, this work provides a theoretical framework for the assessment of key properties of mathematical models before their experimental application. Attention should be paid when applying integrated mPBPK-TMDD models, as identifiability issues do exist, especially when rich study designs are not feasible.

Appendix

Model equations for the four mPBPK-TMDD models (Full, A, B, and C) are here provided. Parameter and variables notations are as introduced in the sections The full mPBPK-TMDD model and Other mPBPK-TMDD models: quasi-steady-state approximations.

Full Model

$$\begin{aligned} C_p=\, & {} A_p/V_p \nonumber \\ \frac{dA_p}{dt}=\, & {} In(t)+C_{lymph} L-C_p L_1 (1-\sigma _1) - C_p L_2 (1-\sigma _2)-C_p C\! L_p \nonumber \\ \frac{dC_{tight}}{dt}= & {} \frac{1}{V_{tight}}\left[ L_1 (1-\sigma _1) C_p - L_1 (1-\sigma _L) C_{tight}\right] \nonumber \\ \frac{dC_{leaky_{free}}}{dt}= & {} \frac{1}{V_{leaky}}\left[ L_2 (1-\sigma _2) C_p - L_2 (1-\sigma _L) C_{leaky_{free}}\right] \nonumber \\&-k_{on} C_{leaky_{free}} R_{leaky_{free}} + k_{off} C\! R_{leaky} \nonumber \\ \frac{dR_{leaky_{free}}}{dt}=\, & {} k_{syn} - k_{deg} R_{leaky_{free}} - k_{on} C_{leaky_{free}} R_{leaky_{free}}+ k_{off} C\! R_{leaky} \nonumber \\ \frac{dC\! R_{leaky}}{dt}=\, & {} k_{on} C_{leaky_{free}} R_{leaky_{free}}- k_{off} C\! R_{leaky} - k_{int} C\! R_{leaky} \nonumber \\ \frac{dC_{lymph}}{dt}=\, & {} \frac{1}{V_{lymph}}[L_1 (1- \sigma _L) C_{tight} + L_2 (1-\sigma _L) C_{leaky_{free}}-C_{lymph} L] \end{aligned}$$

(4)

Model A

$$\begin{aligned} C_p=\, & {} A_p/V_p \nonumber \\ \frac{dA_p}{dt}=\, & {} In(t)+C_{lymph} L-C_p L1 (1-\sigma _1) - C_p L_2 (1-\sigma _2)-C_p C\! L_p \nonumber \\ \frac{dC_{tight}}{dt}=\, & {} \frac{1}{V_{tight}}\left[ L_1 (1-\sigma _1) C_p - L_1 (1-\sigma _L) C_{tight}\right] \nonumber \\ \frac{dC_{leaky_{total}}}{dt}=\, & {} \frac{1}{V_{leaky}}\left[ L_2 (1-\sigma _2) C_p - L_2 (1-\sigma _L) C_{leaky_{free}}\right] -k_{int} C\! R_{leaky} \nonumber \\ \frac{dR_{leaky_{total}}}{dt}=\, & {} k_{syn} - k_{deg} R_{leaky_{free}} - k_{int} C\! R_{leaky} \nonumber \\ \frac{dC_{lymph}}{dt}=\, & {} \frac{1}{V_{lymph}}\left[ L_1 (1- \sigma _L) C_{tight} + L_2 (1-\sigma _L) C_{leaky_{free}}-C_{lymph} L\right] \end{aligned}$$

(5)

where $C_{leaky_{free}}$ and $C\! R_{leaky}$ are computed as:

$$\begin{aligned} C_{leaky_{free}}= & {} \frac{1}{2}(C_{leaky_{total}}-R_{leaky_{total}} - k_{ss} \nonumber \\&+ \sqrt{(C_{leaky_{total}}-R_{leaky_{total}}-k_{ss})^{2}+4 k_{ss} C_{leaky_{total}}}) \nonumber \\ C\! R_{leaky}= & {} \frac{R_{leaky_{total}} C_{leaky_{free}}}{k_{ss}+C_{leaky_{free}}} \end{aligned}$$

(6)

Model B

$$\begin{aligned} C_p= \,& {} A_p/V_p \nonumber \\ \frac{dA_p}{dt}=\, & {} In(t)+C_{lymph} L-C_p L1 (1-\sigma _1) - C_p L_2 (1-\sigma _2)-C_p C\! L_p \nonumber \\ \frac{dC_{tight}}{dt}=\, & {} \frac{1}{V_{tight}}\left[ L_1 (1-\sigma _1) C_p - L_1 (1-\sigma _L) C_{tight}\right] \nonumber \\ \frac{dC_{leaky_{total}}}{dt}=\, & {} \frac{1}{V_{leaky}}\left[ L_2 (1-\sigma _2) C_p - L_2 (1-\sigma _L) C_{leaky_{free}}\right] -k_{int} C\! R_{leaky} \nonumber \\ \frac{dC_{lymph}}{dt}=\, & {} \frac{1}{V_{lymph}}\left[ L_1 (1- \sigma _L) C_{tight} + L_2 (1-\sigma _L) C_{leaky_{free}}-C_{lymph} L\right] \end{aligned}$$

(7)

where:

$$\begin{aligned} \alpha&= k_{int} \nonumber \\ \beta&= k_{ss} k_{deg} - k_{int} C_{leaky_{total}} + k_{syn} \nonumber \\ \gamma&= -k_{ss} k_{deg} C_{leaky_{total}} \nonumber \\ C_{leaky_{free}}&= \frac{1}{2 \alpha }\left( -\beta + \sqrt{\beta ^2 - 4\alpha \gamma }\right) \nonumber \\ R_{leaky_{free}}&= \frac{k_{syn} k_{ss}}{(k_{ss} k_{deg}+k_{int} C_{leaky_{free}})} \nonumber \\ C\! R_{leaky}&= \frac{R_{leaky_{free}} C_{leaky_{free}}}{k_{ss}} \end{aligned}$$

(8)

Model C

$$\begin{aligned} C_p=\, & {} A_p/V_p \nonumber \\ \frac{dA_p}{dt}=\, & {} In(t) + C_{lymph} L - C_p L_1 (1 - \sigma _1) - C_p L_2 (1 - \sigma _2) - C_p C\! L_p \nonumber \\ \frac{dC_{tight}}{dt}=\, & {} \frac{1}{V_{tight}}\left[ C_p L_1 (1-\sigma _1) - L_1 (1-\sigma _L) C_{tight}\right] \nonumber \\ \frac{dC_{lymph}}{dt}=\, & {} \frac{1}{V_{lymph}}\left[ L_1 (1-\sigma _L) C_{tight} + L_2 (1-\sigma _L) C_{leaky_{free}} - C_{lymph} L \right] \end{aligned}$$

(9)

where $C_{leaky_{free}}$, $R_{leaky_{free}}$ and $C\! R_{leaky}$ are obtained as:

$$\begin{aligned} \alpha&= -k_{int} L_2 (1-\sigma _L) \nonumber \\ \beta&= k_{int} C_p L_2 (1-\sigma _2)-k_{ss} k_{deg} L_2 (1-\sigma _L)-k_{int} V_{leaky} k_{syn} \nonumber \\ \gamma&= k_{ss} k_{deg} C_p L_2 (1-\sigma _2) \nonumber \\ C_{leaky_{free}}&= \frac{1}{2\alpha }\left( -\beta - \sqrt{\beta ^2 - 4\alpha \gamma }\right) \nonumber \\ R_{leaky_{free}}&= \frac{k_{syn} k_{ss}}{(k_{ss} k_{deg}+k_{int} C_{leaky_{free}})} \nonumber \\ C\! R_{leaky}&= \frac{R_{leaky_{free}} C_{leaky_{free}}}{k_{ss}}\end{aligned}$$

(10)