Abstract
Increasing the safety demands of various progressively complex structures (e.g., in aerospace, automotive engineering, and wind power technology) and the parallel goal of reducing inspection costs set new objectives in the field of ultrasonics and guided elastic wave measurements. The focus is to deliver applicable sensors attached permanently to a particular structure for on-demand inspections. Piezoelectric fiber patches (PFPs) are known as lightweight and structure-conforming transducers for guided elastic wave generation and detection. We propose a new PFP concept combining advantages of different previous designs. With the new approach, a user can switch between a Lamb wave and a shear horizontal wave excitation by partially changing the polarity of the transducer electrodes. After summarizing the existing PFP variants, the new concept is introduced and experimentally verified by a three-dimensional laser Doppler vibrometer visualization of excited waves. Moreover, the first prototype of the new PFP transducer is presented.
Similar content being viewed by others
1 Introduction
Structural health monitoring (SHM) refers to the process of implementing a damage detection and characterization system for engineering structures based on permanently installed transducers. Numerous physical principles can be used for this purpose. In particular, elastic waves guided in plate- and shell-like structures have been widely applied. In fact, guided elastic waves (GEWs) have already been used in acoustic emissions for the survey of pressure vessels long before the SHM became popular. To excite and detect GEWs, appropriate transducers are required; in most cases, they can act as both a transmitter and receiver.
A few criteria are important for the choice of transducer, including the following:
-
(1)
a small size and mass with negligible effect on the investigated structure.
-
(2)
a relatively low price, especially when a large number of transducers is required, which is typical in many SHM applications.
-
(3)
conformity to the investigated structure, in particular to curved surfaces.
-
(4)
directivity to be sensitive to certain regions of interest, or omnidirectional radiation characteristics for equal sensitivity in all directions (for the survey of large structures).
-
(5)
mode selectivity for the excitation of the most suitable wave modes for damage detection and for reducing the complexity of the received signal evaluation.
Some of the mentioned criteria are also valid for conventional nondestructive testing; however, the first two are specific for SHM, where typically many transducers are permanently attached to the structure.
The main advantage of using GEWs is that they follow slightly curved structures without significant disturbances. For plates and plate-like structures, guided waves can be classified into Lamb and horizontally polarized shear waves. Lamb waves are polarized in the sagittal plane and can exist in two basic types: symmetric (S0, S1, S2, …) and antisymmetric (A0, A1, A2, …). Horizontally polarized shear waves have a vibration direction perpendicular to both the wave propagation direction and the surface normal. Tubes and bars allow for additional modes [1], most of them being dispersive, which means that the propagation velocity depends on the frequency. This dispersion causes unwanted effects, such as the spreading of wave packets, and a difference between the phase and group velocity. The complex mode structure of GEWs together with their dispersion complicate the interpretation of transmitted signals in a GEW-SHM system. Therefore, it is advantageous to limit the signal complexity by exciting and sensing only a limited number of modes—preferentially in their range of week dispersion—and by using the nondispersive SH0 mode. A further simplification can be attained using a distinct transducer directivity. Therefore, mode selective transducers with the desired directivity are required and appear promising for a large number of applications. A directional wave field appears to be particularly useful where objects to be monitored are difficult to access. These include pipelines and storage tanks in the chemical industry and in power plant technology, as well as components made of fiber composite materials in aerospace and wind turbines [2]. Especially for the former case, mode selective transducers appear to be particularly useful regarding the interaction with different damages within the same object. Dispersive Lamb waves can be used to detect changes in wall thickness (corrosion, abrasion, sedimentation, fouling, etc.), whereas the non-dispersive SH0 mode is particularly suitable for crack detection.
Previously, various types of transducers have been proposed for GEW generation and detection. Electromagnetic acoustic transducers generate elastic waves directly in conductive materials such that their application is restricted to metals, in general [3, 4]. Magnetostrictive transducers generate stress in a magnetostrictive layer contained in the transducer. The corresponding strain is transferred via a coupling layer to the specimen [5,6,7,8]. Both transducer types rely on strong static magnetic fields, which render them rather bulky and large in mass. Another option is to excite GEWs by laser [9] and/or detect wave fields by laser Doppler vibrometry [10, 11]. Laser excitation and detection is advantageous for investigating the physical wave propagation of GEWs experimentally. This is especially true if the full vector of the displacement is recorded using a three-dimensional (3D) laser Doppler vibrometer [12, 13].
The types of transducers mentioned thus far are extremely heavy; furthermore, the laser detection is expensive, rendering the specified transducers unsuitable for SHM applications. Compared with those transducers, piezoelectric transducers are lightweight and cheap. Typically, small piezoelectric discs (sometimes called wafers) are glued to the surface [1]. More flexibility (and hence shape compliance) is provided by PVDF foils [14] and different variants of piezoelectric fiber materials [15,16,17,18,19,20]. To utilize the high flexibility and avoid the lower efficiency of PVDF, we will focus on piezoelectric fiber materials in the following.
The objective of this paper is to introduce the reader to piezoelectric fiber composites as transducers for GEW generation and detection, discuss already published designs, and propose a new design with superior flexibility based on that. In Sect. 2.1, we discuss the interaction of piezoelectric active elements with the surface of an object by generating stress fields. This is applied to transducers based on piezoelectric fiber patches (PFPs) (Sect. 2.2). They are made of a piezoelectric fiber/plastic matrix composite, which is encapsulated to form a patch. The early type of PFP has only one layer of parallel fibers and acts preferentially as a Lamb wave transducer. This type is described in Sect. 2.2.1. When interdigital electrodes (IDEs) are grouped to control them individually as in a phased array, different areas of the transducer can be excited independently. Hence, Lamb wave modes are excited selectively and one-sided directivity can be obtained [17]. In these PFPs, the fibers are arranged unidirectionally in one layer and the intended wave propagation direction is parallel to the fibers. In this paper they are called Lamb mode array PFP. Furthermore, horizontally polarized modes can be excited preferentially by another arrangement called shear horizontal piezoelectric fiber patches (SHPHFPs) [21]. We describe these SHPFPs in more detail in Sect. 2.2.2. In Sect. 2.3, we introduce a new PFP configuration by combining the ideas of SHPFPs and Lamb mode array PFPs. This results in a transducer, which is not only a type of array SHPFP similar to the previous Lamb wave array PFP, but also allows the SH mode and Lamb mode operations to be switched. The aim of the present study is not to describe this type of transducer in all its possible variants and characteristics, but to demonstrate how existing principles can be combined to obtain a new transducer type with extended capabilities. The first prototype of the new PFP is presented in Sect. 3. The paper is summarized and conclusions are presented in Sect. 4.
2 Various Options for PFP Transducer Operation
2.1 General Remarks
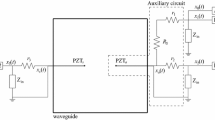
The interactions of piezoelectric structures glued onto the surface of a specimen for generating elastic waves have been discussed in detail in [21]. A summarized discussion is provided herein for convenience (Fig. 1). The total force introduced into the surface of the specimen at the transducer interface is equal to the integral over the surface force density. Either this total force is already zero owing to the type of used piezoelectric element, as in Fig. 1 cases (a), (d) and (e), or it has to be compensated by a counter force, as physics requires. In the thickness mode (b) and thickness-shear mode (c), the counter force is provided by the inertia of a backing mass. Without such a backing mass the only counter force would be the rather weak accelerating force of the deforming piezoelement. As SHM applications require lightweight transducers, additional masses should be avoided. Therefore, we consider the in-plane omnidirectional mode (a), face-shear mode (d) and in-plane unidirectional modes (e) only. Case (a) represents the typical piezoelectric wafer, which has been studied widely (see [1]) and is used in this study as a reference only.

Figure reproduced from [21] with permission from Elsevier (Color figure online)
Surface tractions on a waveguide, exerted by applied piezoelectric wafers. For each situation, the surface tractions are indicated by arrows in the top image and cross section (through the waveguide plus transducer) in the bottom image. The mode notation corresponds to the deformation of the piezoelectric wafer in its free state (see [21]). Thereby, the first index stand for the electric field direction and the second index for the relevant deformation. The Voigt notation is applied for the index (“ii” ≥ I,“33” ≥ “3”, “12” ≥ “6”, etc.). To exert significant tractions, an inertial mass (dark blue) was added in the thickness mode (b) and thickness-shear mode (c). The main wave modes generated in the waveguide are indicated as well.
In the argumentation above, the action of the transducer to the sample is described by the given surface tractions. Strictly speaking this is only correct in the limiting case of a vanishing interaction between transducer and object. In practice they are elastically coupled due to the finite mass and stiffness ratios. Consequently, a multiphysics problem arise, which in most cases can only be solved by numerical simulations [22]. However, situations exist in which the systems are decoupled. In the limiting case of a sample surface, which is stiff compared to the transducer, the transducer can be considered as “clamped” by the sample. The surface tractions generated by the piezoelectric material in the sample can be calculated from analytic expressions. In the other limiting case of a “compliant” sample surface, the transducer is free to move and its displacement will be transferred individually to the sample surface. In both cases, the behavior of the transducer can be calculated without the specimen’s feedback. Hereinafter, the “stiff sample” description is used as it appears to be the most typical case. This approach has been used in a few of our early simulations of GEWs generated by PFPs [23] and in similar investigations by Salas [20]. The discussion will be similar for the other limiting case of the “soft sample.” The intermediate case may be slightly more complex if addressed quantitatively and hence will be studied later numerically and described in a forthcoming publication.
2.2 Summary of Known PFP Transducer Concepts
2.2.1 Lamb Wave Transducer
By dividing a solid piezoelectric material into fibers and forming a 1–3 composite, flexible piezoelectric fiber patches can be fabricated. These transducers were originally invented for adaptronic applications. Several names have been penned for slightly different technological variants. Active fiber composites (AFC) contain round fibers, whereas macrofiber composites (MFCs) contain rectangular-shaped fibers. Additionally, the use of hollow fibers in composites have been proposed. The paper by Williams et al. [24] provides a good overview of the existing variants. Currently, these piezoelectric composites are studied extensively as guided wave transducers.
The ideas discussed in the present study are not restricted to a special variant of piezoelectric fiber composites. Therefore, the general term, PFP is used throughout the manuscript. It is noteworthy that the fiber patch realizations used in the experimental part of this study (see Sect. 3) are based on MFC technology and the transducers were produced by MFC manufacturer, Smart-Material. MFCs exist in two variants. In the “d33” variant, dielectric fibers are poled in the fiber length direction and the electric field is generated by IDEs also in this direction. Meanwhile, the “d31” variant has an electric field oriented perpendicular to the fibers. Hereinafter, only the “d33” version is considered.
The peculiarity of the PFPs as a composite material versus homogeneous piezoelectric wafers is their strong anisotropy in the material property tensor. This concerns the mechanical stiffness, piezoelectric properties, and dielectric constants in particular. As the components of the composite—the piezoelectric fibers and the embedding plastics—differ significantly in terms of material parameters, the anisotropy is also very strong.
As mentioned previously, the PFPs were originally developed and applied for the actuation and active deformation of structures. However, researchers realized soon after that they could be used as a transmitter and/or receiver of GEWs. Brunner [18] demonstrated their use as acoustic emission sensors and as transducers for SHM. The strong anisotropy in the patch properties is reflected in the spatial distribution of the generated wave field. However, the generated wave field depends on the ratio between the transducer dimension and the wavelength. For GEWs, this is a complex subject, as a number of wave modes with different wavelengths are involved. To visualize the complexity of the wave fields, numerical simulation results are presented in Fig. 2. The images show the wave fields generated in a 1.5-mm-thick aluminum plate by three rectangular PFPs of different sizes. For the simulation, the “stiff sample” approximation was used, i.e., the action of the transducer was replaced by surface tractions acting at the end of the fibers in the z-direction. The time history of the applied surface tractions was assumed to be identical to that of the excitation signal which is a raised cosine with two cycles (RC2).
Magnitude of the absolute value of particle velocity across the surface of a 1.5-mm-thick aluminum plate excited by PFPs of different sizes varying from 8 mm × 10 mm (on the left) over 15 mm × 20 mm (center) to 30 mm × 40 mm (on the right). The fiber orientation is in the z-direction and the excitation was realized using an RC2 pulse with a center frequency of 300 kHz for the corresponding surface tractions. The images show the velocity distribution at t = 17.1 µs after the excitation (Color figure online)
The snapshots show that the patch size affects the wave field significantly. A small transducer acts as a dipole of surface tractions (see Fig. 2, left). If the transducer becomes larger, the superposition of the tractions and constructive/destructive interferences will results in an increase and/or decrease of the given mode. Readers from the ultrasonic NDE community might be familiar with the sound field of ultrasonic probes. The main beam of a longitudinal wave probe is a compression wave accompanied by shear waves emanating from the aperture edges. The same principles apply here.
The dependence of the generated wave field on the size of the active PFP was used by Salas and Cesnik [20]. They changed the size of the active PFP area by connecting only a variable part of the IDE to the excitation voltage. Using this approach, they tuned the transducer selectivity to the desired wave modes. In another paper, they used the pronounced directivity of appropriate PFPs to form a composite transducer. They arranged the fibers in a circular PFP radially and used IDE groups to excite selected segments only. By changing the excited segments, they could control the generated waves over the full angular range of 2π. They called this type the composite a long-range variable-direction emitting radar (CLoVER) transducer [19].
It is technologically relatively simple to connect certain IDE groups to the excitation electronics to change both the excited groups and the polarity in this connection. Therefore, it is obvious that the desired wave mode can be enhanced by matching the spatial excitation periodicity with the wavelength by controlling the IDE groups. This was demonstrated by Manka et al. in [25], in which they used PFPs to achieve that accomplished using PZT wavers previously [26].
The results discussed thus far for rectangular transducer realizations enable single wave modes to be selected. However, these modes are always emitted equally from both sides of the transducer. Zhu [27] overcame this problem by dividing the excitation area into regions with a length smaller than λ/2 and by exciting it with a certain time delay between subgroups. This was discussed and demonstrated for piezoelectric wafers and PVDF materials. To the best of our knowledge, these ideas have not been implemented in PFPs.
Moreover, the concepts discussed thus far for mode selection rely on narrowband signals. They generate pulses with a certain length, so that wave parts generated in different areas of the transducer can interfere with each other. If the interest is in short pulses and therefore wideband signals, the concept of time-delayed excitation must be introduced [17]. For enabling independent control, separate external excess to several IDE groups along the propagation direction must be implemented. We call this arrangement the array PFP (A-PFP). Figure 3 shows the numerically calculated displacement in such a PFP, where only one of the IDE groups is excited by a bipolar pulse. Here, the wave propagates in both fiber length directions with opposite polarity. However, if the excitation of all groups moves in one direction with time delays corresponding to the velocity of a given mode, this mode is excited preferentially in the given direction as expected (Fig. 4).

reproduced from [23] with permission from the American Institute of Physics (Color figure online)
ux displacement of a free A-PFP with bipolar excitation of only one IDE group. PFP size 90 mm × 50 mm; active area size 34,5 mm × 20 mm; excitation time 2 µs; snapshots captured at 3.28, 9.85, and 6.42 μs;

These experimental B-scans are reproduced from [23] with permission from the American Institute of Physics (Color figure online)
Upper row: sketch of the A-PFP with the excited IDE group indicated by red and blue; left: only excitation of the rightmost group; right: stacked sketches indicating the time sequence of excitation from right to left; bottom row: B-Scans of the wave fields generated by an A-PFP on a 3 mm PMMA plate, left column: excitation of only one IDE group with an unipolar pulse of duration t = 0.5 µs, middle and right column: successive time delayed excitation of the IDE groups with an RC3 of 100 kHz. The delay is from right to left with a velocity of 1 mm/µs (middle) and 2.4 mm/µs (image on the right) for a preferrd excitation of A0 and S0 modes, respectively. The horizontal and vertical axis in the lower row images are from 0 to 152 mm and from 0 to 100 µs, respectively.
2.2.2 Shear Wave Transducer
As mentioned previously, a number of publications have described piezoelectric wafer transducers for the generation of horizontally polarized shear waves. With appropriate poling and electrodes for the generating electric fields, both face-shear [28,29,30,31,32,33] and thickness-shear are realized [34,35,36]. Additionally, studies describing a method to excite horizontal shear waves with PFPs exist [37, 38]. These studies are based on generating a shear stress in individual fibers, which are poled along the fiber length direction. The electric field is introduced by the IDE orthogonal to the poling, either in the transducer thickness direction or across the fibers in the lateral direction. The first variant should excite the thickness-shear and the second variant face-shear. In our opinion, the thickness-shear might require backing for efficient excitation and the face-shear will be inefficient because the electric field is perpendicular to the fibers. This will result in a considerable reduction in the electric field in the piezomaterial if the field must cross the epoxy from fiber to fiber. The reduction is owing to the significant (approximately three orders of magnitude) ratio of the dielectric constants.
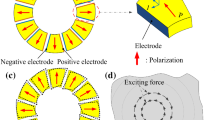
Additionally, special arrangements of d33-mode PFPs can generate pure face-shear [21]. Two fiber layers with orthogonal fiber orientation are combined and operated contrastingly (i.e., when one is extending, the other is contracting). MFCs with a 45° fiber orientation designed for twisting the deformation of parts (Fig. 5 right) were available from Smart Material GmbH. Two patches were stacked one over the other and operated as shown in Fig. 5, left. To demonstrate the excitation of shear waves, a releasable viscous coupling between the two patches in the stack and between the stack and the plate was used in laboratory measurements to keep the individual patches for further experiments. It was verified that strong shear horizontal waves could be excited in this PFP combination, which we called shear horizontal PFP (SHPFP) [21]. The purity defined as the amplitude ratio of the desired SH wave to the unwanted Lamb waves was also investigated [22]. It was shown that the directivity and purity of the SH wave generation could be improved by operating two SHPFP stacks instead of one. The stacks were placed one next to the other, and they were operated in opposite phases.

with permission from Elsevier (left image) and Smart Material GmbH (right image) (Color figure online)
Stacking scheme of two MFC-F1 patches resulting in an SHPFP for pure shear excitation (left picture) [21]. Picture on the right: An MFC-F1 transducer in the twisting operation. It was developed for the twisting operation of objects;
2.3 Concept of a Mode-Switchable PFP
A mode-switchable PFP combines the advantages of the A-PFP and the SHPFP. For this new type of transducer, the orientation between the IDE and fibers must be changed from 90° to 45° such that the IDEs are orientated parallel to the sides of the rectangular patch, and individual IDE groups can be connected separately by external contacts to the electronics. Therefore, horizontal stripe areas of the patch can be excited (see Fig. 6, upper row). The width of the active area of the patch can be affected by the number of finger pairs connected to the electrical excitation. The possibility to change the relative orientation between the piezofibers and IDE electrodes from perpendicular to 45° has been reported in [21] (see Fig. 7 herein) but not yet realized experimentally. We do not have evidence that both arrangements are equivalent but rely on the simple argument that the generated electric fields will follow the fibers. This will occur because of the high ratio between the dielectric constants of PZT and epoxy. The new electrode layout might be slightly less effective compared with the original one, as the electric field path from one electrode to the next is increased by a factor of \(\sqrt{2}\) owing to the 45° arrangement. This results in a correspondingly reduced field. The electric field can be increased again, e.g., by reducing the distance of the IDE correspondingly; however, such an optimization is out of the scope of this paper and is subject to further investigations.
Schematic drawing of both layers for a MS-PFP (upper two rows) with a group of two IDE pairs excited electrically. Arrows indicate the force intensities generated in the layers under clamped conditions. The drawings in the bottom row show the overlay of the layers above with resulting force intensities indicated by arrows. Left: Shear excitation for the generation of SH modes, right: dilatational excitation for the excitation of Lamb modes. The blue arrows in the bottom row images indicate the width of the excited IDE group for preferential excitation of the corresponding wave mode with half the wavelength (Color figure online)
Stresses generated in an MS- PFP when two successive IDE groups are excited with an inverse phase. Left picture: SH wave generation corresponding to the dual SHPFP transducer; picture on the right: excitation of Lamb waves in the vertical direction with wavelength \({\varvec{\lambda}}\) (Color figure online)
In Fig. 6, the upper two rows show both layers of the stack individually, whereas the lower row shows an overlay. Only one group of IDE fingers in the lower part of the layer is charged to demonstrate selective excitation.
In the left column of Fig. 6, the two layers of the stack are excited to obtain a shear excitation. This is equivalent to the SHPFP operation but restricted to a part of the transducer. The blue arrow with λ/2 annotation indicates that the excitation of a shear wave will be the most efficient when the width of the excited area matches half the wavelength of the excited shear wave mode.
Several variants of the proposed design can be obtained. Individual IDE fingers can be combined to a number of electrode groups and connected to external electronics. When these electronics have several independent channels, the transducer can be operated as an array SHPFP. The excitation can be selected freely. Furthermore, the unidirectionality and shear wave mode selectivity can be attained similar to those described in Sect. 2.2.2. for the Lamb wave array PFP. This is at the disadvantage of a high electronic equipment expenditure. However, simpler options exist at the expense of giving up the unidirectionality option, e.g., fixating the wave mode more strictly by prescribing a spatial excitation pattern. The wavelength can be changed simply by reconnecting the finger pairs to smaller or larger groups. The left drawing of Fig. 7 shows an example where a full wavelength λ is inscribed instead of only half of the wavelength. Our new design includes the double SHPFP of [22] with all the advantages reported in that previous publication.
In addition to the abovementioned options from the array-like IDE grouping, the new PFP design enables a switch between face-shear and extensional excitation. This is demonstrated in the right column of Fig. 6. If the polarity of the excitation in one layer is changed, the signature of the forces generated in that layer changes; hence the vector sum of forces generated in both layers changes its orientation by 90°. It is noteworthy that all forces are perpendicular to the excited area (see bottom right drawing of Fig. 6). The force field corresponds to a pure lateral extension; therefore, it will excite (symmetric and antisymmetric) Lamb modes. However, a simple change in polarity in one layer allows switching between shear and Lamb mode excitations. This property justifies the use of the term “mode-switchable PFP” (MS-PFP) for the proposed design. All the array considerations discussed for the face-shear excitation apply for the extensional excitation as well.
3 Experimental Realization and First Proof of Operation
3.1 Design and Realization of the Mode-Switchable PFP
PFPs can be produced using various methods following the concepts mentioned in the preceding section, which differ in their realization details. We herein describe only one of them, which was realized for the basic demonstration of the MS-PFP operation. The drawing in Fig. 8 (left) shows the setup. The two layers of PZT fibers are mechanically connected without a layer of electrodes between them. The electrodes controlling the fibers are immediately above and below this fiber compound. This drawing only demonstrates the main principle; in fact, the number of external connections differs from the actual layout. A photograph of one of the PFPs produced by Smart Material is shown in Fig. 8 (right). The solder pads visible on both sides of the patch clearly indicate the endpoints of the electrodes. Each of the two layers contain 16 electrode pairs. Each electrode pair connects two couples of IDE fingers.
3.2 First Measurement Results
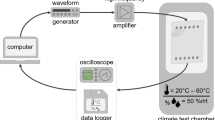
The mode-switchable PFP was attached to a steel plate of thickness 2 mm. The orientation in space was such that the IDE electrodes were orientated vertically. The four furthest left electrode pairs were connected to the IKTS electronics MAS2. This IDE group excited an area of width 7 mm, corresponding to approximately ¼ of the full PFP width of 31 mm. The electrical excitation was performed using a RC3 pulse with center frequency 150 kHz and peak-to-peak voltage 150 V. The waves generated in the steel plate were detected by a Polytec 3D laser Doppler vibrometer. Figure 9 shows the entire measurement setup.
The PFP was coupled to the steel plate by the viscous medium honey and then pressed to it by magnets. Releasable viscous coupling was used such that the patch remained intact for other configurations. No coupling medium was introduced between magnets and the PFP that could transfer shear forces to the magnets. Therefore, we do not expect any significant generation of unwanted waves in the magnets. For subsequently practical applications, the patch will be glued to the substrate to ensure reliable mechanical coupling and to avoid the need for magnets.
Figure 10 presents measurements proving that the new PFP design can preferentially excite both SH and Lamb modes, by only reconnecting (switching) some electrodes. The left column of Fig. 10 shows the x, y, and z particle velocities at time t = 32 µs after excitation. It is clear that the y-component, vy of the velocity is much larger than vx and vz. The wave packet traveling to the left is farther from the center of the PFP as the packet travels to the right. This is in accordance with the excitation of the left quarter of the patch only.
Snapshots of the wave propagation generated in the plate by one group of IDE, switched between SH wave excitation (left column) and extensional Lamb wave excitation (right column). The IDEs are orientated vertically (compare with Fig. 8). The excited IDE group is the furthermost left one. It is noteworthy that the times when the snapshots were captured were different: left column, 32 µs and right column, 25 µs. In addition, the color bar is scaled slightly differently (Color figure online)
In the measurement displayed in the right column of Fig. 10, the contacts of the upper layer were switched to change the polarity in one of the layers. Instead of shear excitation, an extensional excitation was obtained as discussed in Sect. 2.3. Therefore, the x-velocity component is now the largest and shows a clear wave packet. Hence, we present an earlier snapshot (t = 25 µs), where the wave packet is still in the scan field. This is in accordance with the higher wave speed of the S0 mode, which is expected to be observed. The assumption that S0 is displayed is supported by the larger wavelength in the right column compared with the left one.
B-scans generated from the same measured dataset are displayed in Fig. 11. The scan line selected is in the middle of the left scan field, as indicated by the dashed line in Fig. 10. For the shear excitation, a strong vy component was observed (left column, graph in the middle). As shown, a time of 27 µs is estimated for a travel distance of 90 mm. This yields a wave speed of 3.3 mm/µs fitted to the velocity of the SH0 mode in the plate. The apparent dispersion free behavior of the wave—recognizable as the individual phases moves as fast as the entire wave packet—supports this interpretation. This is different for the waves visible in the B-scan of the vz component (left column bottom graph). A weak wave packet is identified therein, which is enclosed by dashed green lines with a wave speed of approximately 2.57 mm/µs. The points of equal phase move with a different velocity of 1.55 mm/µs. Both values are close to that of the A0 mode phase and group velocities obtained from the dispersion diagram of a steel plate of thickness 2 mm at a frequency of f = 150 kHz. The x-component of the velocity (left column, top graph) shows an almost dispersion-free wave with a velocity of approximately 5.6 mm/µs. This fits the S0 wave in the plate. This wave is more pronounced when an extensional excitation is applied (right column top graph). For an extensional excitation, the SH0 wave is visible but with a much smaller amplitude. The A0 wave trains are visible again in the out-of-plane displacement graph (left column, bottom graph). Having identified it in the out-of-plane component (vz) once, the A0 wave trace is easily recognizable in the graph of the vx component as well.
B-scans generated from the same measurement as shown in Fig. 10. The scan line for the B-scans is indicated in the vx snapshot of the shear excitation (upper left image) in Fig. 10. The geometrical arrangement of the different B-scans in the figure is the same as that for the arrangement of the snapshots in Fig. 10. In all images, the linear gray scale represents the same displacement velocity range from − 6 × 10–4 to 6 × 10–4 m/s (Color figure online)
4 Summary and Discussion
Existing PFP transducers can excite Lamb waves and shear horizontal waves bidirectionally. Additionally, by controlling IDE groups in a timely or phase-shifted manner, Lamb waves can be excited unidirectionally and mode selectively. We herein proposed a new concept, the MS-PFP, which combines all mentioned features into one design. The additional advantage is that a change between shear horizontal and Lamb wave excitation can be realized by switching the electrical connections. This connection switching can be performed using multiplexer electronics with only moderate effort. In addition to the idea and basic layout description, a realization was presented together with first measurements of the generated wave fields obtained by 3D laser Doppler vibrometry. The measurements demonstrated the validity of the ideas although they could be further improved. The shear wave was clearly dominant for the shear excitation, while the S0 wave was the strongest in terms of extensional excitation but not as dominant as expected. This momentary drawback was likely because the size of the excited transducer area of 7 mm had not yet matched the half wavelength of the S0 mode, which was estimated to be 19 mm.
We discussed the main operation principles of the MS-PFP and proved its ability to generate waves. However, in practice, the transducer must also function as a receiver. Therefore, all the considerations and experimental work should be repeated for the receiver case, in principle. However, this is not necessary owing to the reciprocity theorem [39]. To be more precise, the theorem has to be adapted to each specific situation, e.g., by specifying the electrical termination and defining what is measured exactly on both the electrical and mechanical sides of the transducer. Depending on the deviations from the necessary conditions, slight differences in the transmission and reception properties are expected. However, we agree with many scholars, in that the reciprocity is fulfilled to a high approximation under normal operating conditions; furthermore, we assumed that this applied to our specific situation. Therefore, in the present study, the investigations were restricted to the excitation case without an explicit consideration of the receiving case.
The MS-PFP has more potential than we could demonstrate in this first paper. We have already discussed the ability to excite groups of elements separately as in an ultrasonic phased array. We did not yet demonstrate the advantage of this array PFP (A-PFP) e.g. in generating unidirectionally directed pure wave modes. However, corresponding experimental and simulation work is in progress and the results will be included in a future paper.
References
Giurgiutiu, V.: Structural Health Monitoring: With Piezoelectric Wafer Active Sensors. Academic Press, Burlington (2007)
Weihnacht, B., Lieske, U., Gaul, T., Tschöke, K.: Handbook of Advanced Non-Destructive Evaluation. Springer Nature Switzerland AG, Berlin (2018)
Thompson, R.B.: Physical principles of measurements with EMAT transducers. Phys. Acoust. 19, 157–200 (1990)
Wilcox, P., Lowe, M., Cawley, P.: Omnidirectional guided wave inspection of large metallic plate structures using an EMAT array. IEEE Trans. UFFC 52, 653–665 (2005)
Kannan, E., Maxfield, B., Balasubramaniam, K.: SHM of pipes using torsional waves generated by in situ magnetostrictive tapes. Smart Mater. Struct. 16, 2505–2515 (2007)
Lee, M.K., Lee, J.S., Young Kim, Y.: An SH wave magnetostrictive patch transducer for ultrasonic inspection of a plate-like structures. In Proceedings of the 2010 IEEE Ultrasonics Symposium (IUS), San Diego, CA, USA, 11–14 October 2010; pp. 1164–1165.
Seung, H.M., Kim, H.W., Kim, Y.Y.: Development of an omni-directional shear-horizontal wave magnetostrictive patch transducer for plates. Ultrasonics 53, 1304–1308 (2013)
Kim, H.W., Lee, J.K., Kim, Y.Y.: Circumferential phased array of shear-horizontal wave magnetostrictive patch transducers for pipe inspection. Ultrasonics 53, 423–431 (2013)
Chia, C.C., Jeong, H.M., Lee, J.R., Park, G.: Composite aircraft debonding visualization by laser ultrasonic scanning excitation and integrated piezoelectric sensing. Struct. Control Health Monit. 19(7), 605–620 (2012)
Köhler, B., & Blackshire, J. L.: Laser vibrometric study of plate waves for structural health monitoring (SHM). In AIP Conference Proceedings (vol. 820(1), pp. 1672–1679). AIP (2006).
Yu, L., Tian, Z.: Lamb wave structural health monitoring using a hybrid PZT-laser vibrometer approach. Structural Health Monitoring 12(5-6), 469–483 (2013)
Barth, M., Köhler, B., Schubert, L.: 3D-Visualisation of Lamb waves by laser vibrometry. In Proceedings of the 4th European Workshop on Structural Health Monitoring 2008, Krakow, 2–4 July 2008; pp. 640–647.
Staszewski, W., Lee, B., Traynor, R.: Fatigue crack detection in metallic structures with Lamb waves and 3D laser vibrometry. Meas. Sci. Technol. 18(3), 727–739 (2007)
Monkhouse, R., Wilcox, P., Cawley, P.: Flexible interdigital PVDF transducers for the generation of Lamb waves in structures. Ultrasonics 35, 489–498 (1997)
Mańka, M., Rosiek, M., Martowicz, A., Stepinski, T., Uhl, T.: Lamb wave transducers made of piezoelectric macro-fiber composite. Struct. Control Health Monit. 20, 1138–1158 (2013)
Schubert, L., Barth, M., Klesse, T., Köhler, B., Frankenstein, B.: Guided elastic waves and their impact interaction in CFRP structures characterized by 3D laser scanning vibrometry. In Proceedings of the 15th International Symposium on: Smart Structures and Materials Nondestructive Evaluation and Health Monitoring 2008, San Diego, 9–13 March 2008.
Köhler, B., Schubert, F., Barth, M., Frankenstein, B.: Selective excitation and detection of Lamb waves for SHM applications. In Proceedings of the Fourth European Workshop on Structural Health 2008, Krakow, July 2–4, 2008; pp. 706–714
Brunner, A.J., Barbezat, M., Huber, C., Flüeler, P.H.: The potential of active fiber composites made from piezoelectric fibers for actuating and sensing applications in structural health monitoring. Mater. Struct. 38(5), 561–567 (2005)
Salas, K.I., Cesnik, C.E.: Guided wave excitation by a CLoVER transducer for structural health monitoring: theory and experiments. Smart Mater. Struct. 18(7), 075005 (2009)
Salas, K.I., Cesnik, C.E.: Design and characterization of a variable-length piezocomposite transducer for structural health monitoring. J. Intell. Mater. Syst. Struct. 21(3), 349–360 (2010)
Köhler, B., Gaul, T., Lieske, U., Schubert, F.: Shear horizontal piezoelectric fiber patch transducers (SH-PFP) for guided elastic wave applications. NDT E Int. 82, 1–12 (2016)
Kim, Y., Gaul, T., Köhler, B.: Improved SH0 guided wave transducers based on piezoelectric fiber patches. Sensors 19(13), 2990 (2019)
Koehler, B., Frankenstein, B., Schubert, F., Barth, M.: Novel piezoelectric fiber transducers for mode selective excitation and detection of lamb waves. AIP Conf. Proc. 1096, 982–989 (2009)
Williams, R. B., Park, G., Inman, D. J., & Wilkie, W. K.: An overview of composite actuators with piezoceramic fibers. In Proceeding of IMAC XX, 47 (2002).
Mańka, M., Martowicz, A., Rosiek, M., Stepinski, T., Uhl, T.: Tunable interdigital transducers made of piezoelectric macro-fiber composite. Smart Mater. Struct. 25(11), 115022 (2016)
Mańka, M., et al.: PZT based tunable Interdigital Transducer for Lamb waves based NDT and SHM. Mech. Syst. Signal Process. 78, 71–83 (2016)
Zhu, W., Rose, J.L.: Lamb wave generation and reception with time-delay periodic linear arrays: a BEM simulation and experimental study. IEEE Trans. Ultrasonics Ferroelect. Freq. Control 46(3), 654–664 (1999)
Zhang, S., Jiang, W., Meyer Jr., R.J., Li, F., Luo, J., Cao, W.: Measurements of face shear properties in relaxor-PbTiO3 single crystals. J. Appl. Phys. 110, 064106 (2011)
Kamal, A., Giurgiutiu, V.: Shear horizontal wave excitation and reception with shear horizontal piezoelectric wafer active sensor (SH-PWAS). Smart Mater. Struct. 23, 085019 (2014)
Zhou, W., Li, H., Yuan, F.: Fundamental understanding of wave generation and reception using d 36 type piezoelectric transducers. Ultrasonics 57, 135–143 (2015)
Miao, H., Dong, S., Li, F.: Excitation of fundamental shear horizontal wave by using face-shear (d36) piezoelectric ceramics. J. Appl. Phys. 119, 174101 (2016)
Miao, H., Huan, Q., Li, F.: Excitation and reception of pure shear horizontal waves by using face-shear d24 mode piezoelectric wafers. arXiv2016, arXiv:1604.03765.
Miao, H., Huan, Q., Wang, Q., Li, F.: A new omnidirectional shear horizontal wave transducer using face-shear (d 24) piezoelectric ring array. Ultrasonics 74, 167–173 (2017)
Boivin, G., Viens, M., Belanger, P.: Development of a low frequency shear horizontal piezoelectric transducer for the generation of plane SH waves. AIP Conf. Proc. 1706, 030019 (2016)
Huan, Q., Miao, H., Li, F.: A nearly perfect omnidirectional shear-horizontal (SH) wave transducer based on a thickness poled, thickness-shear (d15) piezoelectric ring. arXiv2017, arXiv:1704.03629.
Belanger, P., Boivin, G.: Piezoceramic omnidirectional transduction of the fundamental shear horizontal guide wave mode. In Nondestructive Characterization and Monitoring of Advanced Materials, Aerospace, and Civil Infrastructure; International Society for Optics and Photonics: Bellingham, 2016; Volume 98040.
Yin, C. C., & Tsai, W. C.: Flexible ultrasonic transducers for transverse horizontal plate waves. In 2015 IEEE International Ultrasonics Symposium (IUS) (pp. 1–4). IEEE (2015).
Yin, C., Chiu, C., Tsai, W., & Chen, J. (2016). Flexible transducers for guided wave structural health monitoring of porous composite plates. In Proceeding of the 19th World Conference Non-Destruct. Test. (pp. 1–8).
Auld, B.: General electromechanical reciprocity relations applied to the calculation of elastic wave scattering coefficients. Wave Motion 1, 3–10 (1979)
Acknowledgements
Open Access funding provided by Projekt DEAL. This work was funded in part by the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska–Curie grant agreement N. 722134—NDTonAIR. We thank the company, Smart Material for intense discussions and the supply of the mode-switchable PFP prototype.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Köhler, B., Kim, Y., Chwelatiuk, K. et al. A Mode-Switchable Guided Elastic Wave Transducer. J Nondestruct Eval 39, 45 (2020). https://doi.org/10.1007/s10921-020-00690-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10921-020-00690-5