Introduction

COVID-19 is an ongoing pandemic caused by SARS-CoV-2 virus and was detected in Wuhan city of China in Dec 2019 [1]. Severe illness by this virus has no effective treatment or vaccine to date. By 15th August 2020, nearly 21.2 million cases were globally infected causing 767,000 deaths https://www.worldometers.info/coronavirus/. The symptoms of COVID-19 include fever and dry coughing due to acute respiratory infections. It was considered that the main mode of transmission for SARS-CoV-2 is through saliva droplets or nasal discharge https://www.who.int/health-topics/coronavirus#tab=tab 1.

Lungs may be severely affected by coronavirus and abnormalities reside mostly in the inferior lobes [2,3,4,5,6,7,8,9,10]. The congestion in the lungs is visible in the lung Computer Tomography (CT) scans. It is, however, difficult to differentiate it from interstitial pneumonia, or other lung diseases and manual classification may be biased depending on expert’s opinion. Hence there is an urgent need to classify and characterize the disease using an automated Computer-Aided Diagnostics (CADx), as it offers high accuracy due to low inter- and intra-observer variability [11, 12]. Further, one can use CADx to locate the disease in lung CT correctly without any bias [13].

After the outbreak of COVID-19 (COVID) many research groups have published Artificial Intelligence (AI)-based programs for automatic classification of COVID patients against Controls (or asymptomatic patients) [14]. Deep Learning (DL) [15,16,17,18,19,20] is a branch of AI that was mostly used for COVID classification. There are many research studies using Transfer Learning (TL)-based [21,22,23,24,25,26].

approaches, which is also a part of DL. Machine Learning (ML) is another class of AI which is also very useful in medical diagnosis [27,28,29,30]. Thus, automated systems can be developed using ML methods such as Artificial Neural Networks (ANN), decision tree (DT), random forest (RF), which are popular once. More important in lung CT COVID analysis is to know which part of the CT lung is most affected by COVID. Few studies have been published [2, 3], but they are not automated strategies for COVID severity locations (CSL). Thus, there is a clear need for a simple classification paradigm while being able to identify CSL.

Deep learning and transfer learning-based solutions can learn features automatically using their hidden layers and are generally trained on supercomputers to save training time. ML-based systems can also achieve higher accuracy when optimized with powerful feature extraction and selection methods [31, 32]. Also, if the extracted manual feature is rightly chosen, one can achieve higher accuracy for classification and able to characterize the disease [33]. Due to above the reasons, we hypothesize that DL and TL systems are relatively superior to ML.

This study presents nine kinds of AI-models. First, one DL based CNN, five deep learning-based transfer learning methods namely VGG16, DenseNet121, DenseNet169, DenseNet201, and MobileNet. The remaining three kinds of machine-learning (ML) models namely artificial neural network (ANN), decision tree (DT), and random forest (RF) were designed for classification of CT segmented lung COVID against Controls.

As part of the tissue characterization system, we attempt three kinds of novel tissue characterization subsystems for pinpointing the location of COVID severity. This includes (a) Block imaging for COVID severity location; (b) Bispectrum analysis; and (c) Block entropy. This Block imaging describes a novel approach of dividing the lungs into grid-style blocks; it detects the COVID severity of disease in each block and displays it to the user in the form of color-coded blocks to identify the most infected parts of the lungs. Higher-Order Spectra (HOS) [34] was also introduced which is a powerful strategy to detect the presence of disease congestion in the lungs of COVID patients. Further, since the ground glass opacities are fuzzy in nature and cause randomness in the lungs, we compute entropy as part of the tissue characterization system. Performance evaluation of the system was computed using diagnostics odds ratio (DOR) [35] and receiving operating curves (ROC) curve.

The rest of the paper is organized as follows: Section 2 contains the related work in COVID-19 classification. Section 3 contains methods and materials description. Section 4 contains results, while section 5 presents the lung tissue characterization. Section 6 discusses the performance evaluation, followed by a discussion in section 7. Finally, the paper concludes in section 8.

Background literature

Several research studies describe the process of identifying COVID-19 based on CT scan images. Most of these studies use lung segmentation prior to classification. Zhang et al. [21] have described lung segmentation using the DeepLabv3 model. As part of the classification, the authors used a multi-class paradigm having three classes: COVID-19, common pneumonia, and normal. Authors have used 3D ResNet-18 and obtained a classification accuracy of 92.49% with an AUC of 0.9813. Similarly, Wang et al. [22] have used DenseNet 121 for the creation of a lung mask to segment the lungs. Subsequently, authors have used DenseNet like structure for the classification of normal and COVID patients and achieved an AUC of 0.90, with sensitivity and specificity of 78.93%, and 89.93%, respectively.

Oh et al. [23] had used X-ray images and segmented lungs using fully connected DenseNet by getting a lung mask and then separating the lungs from X-ray images. For classification, the authors have randomly chosen several patches of size 224 × 224 covering the lungs from the segmented lungs and train ResNet18. During the prediction process, the authors chose randomly K patches and based on majority voting of classification results authors were able to predict the presence or absence of COVID-19 disease. The authors have shown an accuracy of 88.9% on the testing data set.

Yang et al. [24] had used CT scan images and initially identified the pulmonary parenchyma area by lung segmentation and used DenseNet for classification that gave an accuracy of 92% with an AUC of 0.98 on the test set. Wu et al. [25] have used lung regions extracted as nodules and no nodules using radiologist’s annotations and then used four different methods to classify between the two classes using 10-fold cross-validation. Authors tested on Curvelet and SVM, VGG19, Inception V3, and ResNet 50 and further obtained the best accuracy of 98.23% with AUC of 0.99.

Pan et al. [2] have shown how to estimate the severity of lung involvement in COVID-19. The authors have given scores to each of the five lung lobes visually on a scale of 0 to 5, with 0 indicating no involvement and 5 indicating more than 75% involvement. The total CT score was determined as the sum of lung involvement, ranging from 0 (no involvement) to 25 (maximum involvement). The study showed that inferior lobes were more inclined to be involved with higher CT scores in COVID-19 patients.

Wong et al. [3] used a severity index for each lung. The lung scores were summed to produce a final severity score. A score of 0–4 was assigned to each lung depending on the extent of involvement by consolidation. The scores for each lung were summed to produce the final severity score. The authors found that Chest X-ray findings in COVID-19 patients frequently showed bilateral lower zone consolidation.

Methodology

Patient demographics and data acquisition

COVID disease and Control patients’ data were collected using CT scans from a pool of 60 patients (30 COVID patients with age in the range of 29–85 years (21 males and 9 females) and 30 Control patients. Real-time reverse transcriptase-polymerase chain reaction (RT-PCR assay with throat swab samples) tests were done to confirm COVID disease patients. The control group was completely normal and reviewed by the experienced radiologist. 17 out of 60 (i.e., 28%) patients died who were suffering from ARDS due to COVID-19. The Acute respiratory distress syndrome can be caused by different pathologies but in the cases which we have included was due to the COVID-19 and it was the cause of death. Other cases with ARDS determined by other types of pathologies (cardiac impairment, cardiac pretension, etc.) were not included. The age was in the range of 17–93 years (9 males and 21 females) and the data was collected during March–April 2020 (approval was obtained from the Institutional Ethics Committee, Azienda Ospedaliero Universitari (A.O.U.), “Maggiore d.c.” University of Eastern Piedmont, Novara, ITALY.

Data acquisition

All chest CT scans were performed during a single full inspiratory breath-hold in a supine position on a 128-slice multidetector-row CT scanner (Philips Ingenuity Core, Philips Healthcare, Netherlands). No intravenous or oral contrast media were administered. The CT examinations were performed at 120 kV, 226 mAs (using automatic tube current modulation – Z-DOM, Philips), 1.08 spiral pitch factor, 0.5-s gantry rotation time, and 64*0.625 detector configurations. One-mm thick images were reconstructed with soft tissue kernel using a 512 × 512 matrix (mediastinal window) and with lung kernel using a 768 × 768 matrix (lung window). CT images were reviewed on the Picture Archiving and Communication System (PACS) workstation equipped with two 35 × 43 cm monitors produced by Eizo, with 2048 × 1536 matrix. The data comprised of 20–35 slices per patient giving 990 CT scans for Controls and 705 CT scans for COVID patients. A grid of five sample Control patients’ original grayscale lung CT scans is shown in Fig. 1, while a similar pattern for the COVID patients is shown in Fig. 2.

Fig. 1
figure 1

Five sample Control patients (representing five rows) showing original raw grayscale CT slices

Full size image
Fig. 2
figure 2

Five COVID sample patients (representing five rows) original grayscale images

Full size image

Baseline characteristics

The baseline characteristics of the Italian cohort’s COVID-19 data are presented in Table 1. We have utilized the MedCalc package to perform a t-test on the data, with the level of significance set to P < =0.05. The table shows the essential characteristic traits of CoP patients.

Table 1 Baseline characteristics of CoP and NCoP patients
Full size table

Lung CT segmentation

Several methods for lung CT segmentation have been developed by our group previously [11, 36, 37]. These methods were mainly for lung segmentation followed by risk stratification due to cancer. For simplicity, we used the following steps to segment the lung: (i) A lung mask creation tool was utilized from Neuroimaging Tools and resource collaboratory called “NIHLungSegmentation” tool for creating the masks of lungs in DICOM format using original DICOM CT scans. (ii) The original CT scans and masks in DICOM format were converted to PNG format using software called “XMedCon” [38]. (iii) The PNG masks were refined by using image processing closing operation to smoothen the masks. (iv) Smoothened masks were then used to segment lungs from original grayscale PNG formed in the previous step. Thus, using original CT scans, a lung mask for COVID and Control patients was generated. A sample grayscale image, its mask, and segmented lung are shown in Fig. 3. A grid of five sample Control and COVID patients’ masked lungs is shown in Figs. 4 and 5, respectively.

Fig. 3
figure 3

Sample Control patient’s a original grayscale image, b lung mask, c segmented lung; Sample COVID-19 patient’s d original grayscale image, e lung mask, f segmented lung

Full size image
Fig. 4
figure 4

Five sample Control patients (shown in five rows) with colored segmented lungs

Full size image
Fig. 5
figure 5

Five sample COVID patients (shown in five rows) with colored segmented lungs

Full size image

Deep learning architecture

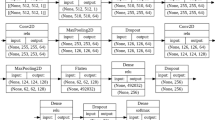
A deep-learning convolution neural network (CNN) was designed with an input convolution layer having 32 filters followed by max-pooling layer. This was adapted due to its simplicity. These were followed by another convolution layer of 16 filters followed by a max-pooling layer. In their succession was a flatten layer to convert the 2-D signal to 1-D and then another dense layer of 128 nodes. Finally, a softmax layer was present with two nodes for classification in two classes Control and COVID. The architecture of deep learning-based CNN thus has a total of 7 layers mainly adapting for simplicity. The diagrammatic view is shown in Fig. 6.

Fig. 6
figure 6

Deep learning architecture of CNN

Full size image

Transfer learning architectures

Transfer learning is a mechanism to use already trained networks on a certain dataset and further calibrate them for desired needs. For example, a person knowing to ride a bicycle can use the learning and learn riding motorbike using that learning. In this study five such pre-trained networks have been used namely, VGG16, DenseNet121, DenseNet169, DenseNet201, and MobileNet. These networks have been trained on famous ImageNet dataset and by adding an extra softmax layer of two nodes at the end of the network we can make them functional for our COVID classification. The architectures of these models are shown in Appendix I (Fig. 26, 27, 28 ,29 and 30). A comparison of different DL/TL models (1 DL and 5 TL) in terms of layers is shown in Table 2.

Table 2 A comparison of number of different layers in 5 TL models and 1 proposed CNN
Full size table

Machine learning architecture and experimental protocols

The ML-architecture for classification of COVID and Control patients is shown in Fig. 7. It consists of two parts: offline system and online system. The offline system consists of two main steps: (a) training feature extraction and (b) training classifier design to generate the offline coefficients (covered by dotted box on the left). The online system also consists of two main steps: (a) online feature extraction and (b) class prediction (Control or COVID). Such a system has been developed by our group before for tissue characterization for different applications such as liver cancer [39,40,41], thyroid cancer [42,43,44], ovarian cancer [45,46,47], atherosclerotic plaque characterization [48,49,50,51,52,53], and lung disease classification [37]. The classification of lungs into COVID and Control was implemented using three ML methods namely ANN, DT, and RF.

Fig. 7
figure 7

Machine learning architecture showing the offline and online system

Full size image

Experimental protocol

Protocol 1: Accuracy using K-fold cross-validation protocol

Different K-fold cross-validation protocols were executed to test the accuracy of the system. K-fold cross-validation uses run time split of data into training and testing based on a split ratio and the system was trained using the training part and later tested using the testing images. The system adapted five kinds of features that were used in training and testing ML classifiers namely Haralick [39], HOG, Hu-moments [47], LBP [54, 55], and GLRLM features. The features were added one-by-one at a time to run K-fold protocols: K2, K4, K5, and K10. The following set of mean parameters was further calculated to assess the system performance as given in Eq. 1, 2, 3, and 4.

$$ \overline{A}\left(\mathrm{c}\right)=\frac{\sum \limits_{\mathrm{f}}^{\mathrm{F}\ }\ \sum \limits_k^{\mathrm{K}\ }\ \sum \limits_i^{{\mathrm{C}}_{\mathrm{o}}}A\ \left(\mathrm{c},\kern0.75em \mathrm{f},\kern0.75em \mathrm{k},\kern0.75em \mathrm{i}\right)}{F\times K\times {C}_o} $$
(1)

Where, Ᾱ(c)is the accuracy for a classifier for a set of features (f) and different K-fold cross-validation protocols (k) and a combination number of K-fold protocol (i).

$$ \overline{A}\left(\mathrm{f}\right)=\frac{\sum \limits_{\mathrm{c}}^{{\mathrm{C}}_{\mathrm{l}}\ }\ \sum \limits_k^{\mathrm{K}\ }\ \sum \limits_i^{{\mathrm{C}}_{\mathrm{o}}}A\ \left(\mathrm{c},\kern0.75em \mathrm{f},\kern0.75em \mathrm{k},\kern0.75em \mathrm{i}\right)}{C_l\times K\times {C}_o\ } $$
(2)

Where Ᾱ(f)is the accuracy for a feature for a set of classifiers (c) and different K-fold cross-validation protocols (k) and the combination number of K-fold protocol (i).

$$ \overline{A}\left(\mathrm{k}\right)=\frac{\sum \limits_{\mathrm{c}}^{{\mathrm{C}}_{\mathrm{l}}\ }\ \sum \limits_{\mathrm{f}}^{\mathrm{F}\ }\ \sum \limits_i^{{\mathrm{C}}_{\mathrm{o}}}A\left(\mathrm{c},\kern0.75em \mathrm{f},\kern0.75em \mathrm{k},\kern0.75em \mathrm{i}\right)}{C_l\times F\times {C}_o} $$
(3)

Where Ᾱ(k)is the accuracy for any K-fold protocol for a set of classifiers (c) and different features (f) and the combination number of K-fold protocol (i).

$$ {\overline{A}}_{\mathrm{sys}}=\frac{\sum \limits_{\mathrm{c}}^{{\mathrm{C}}_{\mathrm{l}}\ }\ \sum \limits_{\mathrm{f}}^{\mathrm{F}\ }\ \sum \limits_k^{\mathrm{K}\ }\ \sum \limits_i^{{\mathrm{C}}_{\mathrm{o}}}A\left(\mathrm{c},\kern0.75em \mathrm{f},\kern0.75em \mathrm{k},\kern0.75em \mathrm{i}\right)}{C_l\times F\times K\times {C}_o} $$
(4)

Where Ᾱsys is the system mean accuracy for any set of classifiers (c), features (f), K-fold protocols (k), and combination number (i) Cl is the number of classifiers equal to 3, F is the feature set equal to 3, K is the number of partition protocols equal to 4 and Co is the number of combinations for a particular K-fold protocol. The symbol A is used for accuracy in Eqs. (1)–(4). The results were analyzed based on (a) accuracy, (b) area under the curve (AUC) and (c) diagnostics odds ratio (DOR), which will be discussed in performance evaluation section.

Results

DL and TL classification results

The deep learning architecture as explained in section 3.3 was used for classification of Control vs. COVID. The K10 cross-validation protocol was used that gave the accuracy of 99.41 ± 5.12%, with an AUC of 0.991 (p < 0.0001). We used five transfer learning methods namely VGG16, DenseNet121, DenseNet169, DenseNet201 and MobileNet as described in section 3.4. The best accuracy was obtained by DenseNet121: 91.56 ± 4.16% with an AUC of 0.913, p < 0.0001, followed by MobileNet: 90.93 ± 3.59%, with an AUC of 0.893, p < 0.0001, DenseNet201: 87.49 ± 0.66%, with an AUC of 0.871, p < 0.0001, DenseNet169: 85.93 ± 8.27%, with an AUC of 0.852, p < 0.0001, and VGG16: 71.87 ± 12.67%, with an AUC of 0.714, p < 0.0001. These results were obtained using the K10 cross-validation protocol. A plot of mean accuracy along with their standard deviations of five transfer learning models is shown in Fig. 8.

Fig. 8
figure 8

Mean accuracies of five different transfer learning models

Full size image

ML classification results

As detailed in section 3.5, three ML classifiers ANN, DT and RF were executed on the entire dataset using five features (i) LBP, (ii) Haralick, (iii) Histogram of oriented gradients (HOG), (iv) Hu-moments and (v) Gray Level Run Length Matrix (GLRLM). These 5 × 3 sets of feature combinations and classifiers were executed for four K-fold cross-validation protocols (K2, K4, K5, and K10) and mean accuracy was calculated for each combination with a K-fold protocol. The best K10 mean accuracy was noticed for the Random Forest model by including all the five features leading to 99.41 ± 0.62%, having an AUC of 0.988, (p < 0.0001) followed by DT including all the five features: 95.88 ± 1.30%, 0.948 (p < 0.0001). The accuracy of ANN was also best with all five features, 87.31 ± 4.79%, 0.861 (p < 0.0001). A comparison plot of ML, TL and DL accuracies is given in Fig. 9.

Fig. 9
figure 9

Comparison of 9 AI models with increasing order of classification accuracies. ML methods shown in green, TL methods are shown in red, and DL method shown in blue. K10 protocol was executed for these accuracies

Full size image

Mean accuracies of 3 ML classifiers based on Eqs. (1–4) are shown in Appendix II (Fig. 31, 32, 33 and 34).

COVID separation index

COVID Separation Index (CSI) is mathematically defined as:

$$ \mathrm{CSI}=\left(\frac{\left|\ {\upmu}_{\mathrm{COVID}}-{\upmu}_{\mathrm{Control}}\right|}{\upmu_{\mathrm{Control}}}\right)\times 100 $$
(5)

where μCOVID is the mean feature value for COVID block and μControl is the mean feature value for Control blocks. CSI for the different set of features is shown in Table 3. As seen in Table 3 all the features have similar CSI in range 35–50. If these values are high, this reflects the changes of higher classification accuracy.

Table 3 CSI for the different set of features
Full size table

Tissue characterization of COVID-19 disease

Characterization method-I: Block imaging

Spatial gridding process

Lungs infected due to SARS-CoV-2 shows regions of hyperintensity in certain regions. An effort was thus made to identify the lung region which was most affected. The segmented lungs were divided into 12 blocks consisting of 3 rows each having 4 blocks, spanning left and right lungs. The pictorial representation of this grid on the segmented lungs for the sample Control and COVID patient is shown in Fig. 10.

Fig. 10
figure 10

Division of segmented lungs into 12 blocks of a Control and b COVID patient

Full size image

Stacking concept mutually exclusive for each block

Figure 11 shows a conceptual stack of all blocks of a particular location of the grid (say for (3,1) shown in Fig. 20) for Control and COVID patients which is used to calculate K10 classification accuracy and CSI values. These values are used to calculate block score and finally its severity value in the form of a probability. Since there are 12 blocks in the grid, there will be 12 such vectors each corresponding to that grid location. This vector will be the stack of all the patients for Control and COVID combination, which will be used for feature extraction.

Fig. 11
figure 11

Process flow of calculating the probability of COVID severity for each blocks (Courtesy of AtheroPoint™, CA, USA)

Full size image

Scoring concept for each block and its probability computation

Given the ML accuracy and CSI values, one then computes the score for each block corresponding to the feature selected (f) and classifier selected (c). Points are assigned to each block depending upon the location in the 2 × 2 quadrant of the “classification accuracy vs. COVID separation index” plot. This is shown in Fig. 12, where values are assigned to each quadrant ranging from 1 to 4. The block values are then assigned colors depending upon the probability computed. Color changes are assigned from red, pink, orange, cream, yellow, light green, dark green as per the probability maps per block.

Fig. 12
figure 12

The division of classification accuracy vs. COVID separation index graph into 4 quadrants and points for each quadrant

Full size image

Overall architecture of the block imaging system

The overall system architecture of the Block imaging system for COVID severity computation is shown in Fig. 13. The two main blocks are (a) the probability map computation and (b) color coding. Note that, since there are four partition protocols, three sets of features, three set of classifiers, and a set of 12 blocks for Block imaging, therefore, there are 4× 12× 3× 3 (432) block points. Thus, for each combination of training protocol “k” and each set of classifier “c”, we get a probability map. Therefore, there will be 4 × 3 = 12 probability maps. Technically we get 36 block points for each combination of “k, c”.

Fig. 13
figure 13

Architecture design of the Block Imaging strategy for COVID disease characterization

Full size image

COVID severity computation algorithm

These individual blocks were passed through K-fold protocols to find the accuracy and COVID separation index (CSI) for all features and classifiers combinations. Based on these values a severity probability is calculated for each block and color code is given to each probability starting from red with the highest probability and green lowest. This type of graph was created for all 3 classifiers and the graph was divided into 4 quadrants with points being given to a block depending on the quadrant they lie.

The pseudo code for the block severity is shown as follows:

figure a

Results of accuracy vs. CSI computation on different blocks

The entire database of Controls and COVID was segmented into lung blocks and each block was analyzed in terms of K10 accuracy of RF, DT, and k-NN classifiers. Each block mean features were also calculated and the COVID separation index (CSI) was calculated for different sets of features using Eq. 5. The sets of features used were: Haralick with LBP, Hu-moments with Haralick and LBP with Hu-moments. A graph of accuracy vs. CSI was plotted for each classifier with one of 3 sets of features as shown in Fig. 14.

Fig. 14
figure 14

A plot of accuracy vs. CSI using RF classifier with Hu-moments and Haralick features for all blocks

Full size image

On giving points to each block in this way the final probabilities were calculated independently for each classifier and a color code was given to each block. The block with the highest probability was given a bright red color and then orange and then yellow and then green. The points and probability of each block for RF are given in Table 4. A sample diseased patient color-coded image for k-NN, DT, and RF is shown in Fig. 15. These clearly show that maximum COVID severity is in lower right lung regions. More figures of color-coded images for different classifiers and protocols are given in Appendix III (Fig. 35, 36, 37, 38, 40 and 41). The mean probability values for all blocks for different partition protocols are given in Appendix III (Table 10) and for different classifiers are given in Appendix III (Table 11).

Table 4 Points to each block and combined probability of each block
Full size table
Fig. 15
figure 15

a A sample grayscale diseased image, Color-coded blocks of diseased lung using b k-NN, c DT, and d RF

Full size image

Characterization method-II: Bispectrum analysis

The Bispectrum is a useful measure of the Higher-Order spectrum (HOS) for analyzing the non-linearity of a signal. Several applications of HOS have been published by our group for tissue characterization [44, 56,57,58,59].

COVID lungs have an extra white congestion area these pixels were separated and passed to Radon transform which was used as a signal for higher-order spectrum (HOS) based Bisprectrum (B) calculation. The Bispectrum are powerful tools to detect the non-linearity in the input signal [60, 61]. Radon transform becomes highly nonlinear when there is a sudden change in grayscale image density. Thus, COVID images are characterized with the help of higher B values. The equation for Bispectrum is as given in Eq. 6.

$$ \mathrm{Bispectrum}\left(\mathbf{B}\left(\mathrm{f}1,\mathrm{f}2\right)\right)=\mathrm{E}\left[\mathcal{F}\left(\mathrm{f}1\right)\times \mathcal{F}\left(\mathrm{f}2\right)\times \mathcal{F}\left(\mathrm{f}1+\mathrm{f}2\right)\right] $$
(6)

where, B is the Bispectrum value, \( \mathcal{F} \) is the Fourier transforms and E is the expectation operator. The region Ω of computation of bispectrum and bispectral features of a real signal is uniquely given by a triangle 0 < = f2 < = f1 < = f1 + f2 < = 1.

The images were found to have more diseased pixels in the range 20–40 intensity thus a radon transform of these pixels were taken to transform an image in the form of a signal which was passed to Bispectrum function and 2-D and 3-D plots were created for Control and COVID classes. As expected, the B-values for COVID class were much higher due to several diseased pixels in these images. The 2-D and 3-D plots of Bispectrum for two classes are shown in Figs. 16 and 17.

Fig. 16
figure 16

Comparison of Bispectrum 2-D plots for a Control and b COVID class

Full size image
Fig. 17
figure 17

Comparison of Bispectrum 3-D plots for a Control and b COVID class

Full size image

Characterization method-III: Block entropy

As explained in section 6.1 the lungs were divided into 12 blocks using a grid. The same blocks were used to compute the entropy of each block for Controls and COVID. This process was used to show that there is greater chaotic (or randomness) in certain parts of diseased lungs due to the presence of white regions of congestion. The equation for entropy is as given in Eq. 7.

$$ \mathrm{Entropy}=-{\sum}_{\mathrm{i}=0}^{\mathrm{N}}{\mathrm{p}}_{\mathrm{i}}\log \left({\mathrm{p}}_{\mathrm{i}}\right) $$
(7)

Where pi is the probability of any pixel intensity i in the input image and N is the total number of intensity levels in the grayscale image equal to 255. Entropy is a useful measure of showing the texture of images [37, 44, 60]. If the image has more roughness then it will have higher entropy [47, 62]. The entropy was calculated for each block as shown in Fig. 12. A plot was made for entropies of blocks of Control and COVID class as shown in Fig. 18. As seen the entropy of blocks of lower regions of lungs is higher than Control due to disease regions more prominent in the lower part of the lungs. The percentage increase in entropy for the COVID class is shown in Table 5.

Fig. 18
figure 18

Comparison of block-wise entropy for Control and COVID disease classes

Full size image
Table 5 The percent gain in entropy of disease lung shows higher values in the lower part of the lungs
Full size table

Validation of block imaging

The COVID severity was computed for each block in the grid and a mean was taken for all the blocks to find the overall COVID severity of a patient. All the slices of a particular patient were fed to an ML system trained on all patients except that patient and using Block Imaging algorithm described above its block-wise severity was calculated. Further, the mean of all blocks was computed. Evaluating in this fashion and comparing it with Ground Glass Opacity (GGO) values of CT scans of all patients it was found that the two series had a correlation coefficient of 0.9145 (p < 0.0001). Similarly, correlation of COVID severity with Bispectrum values (Bispectrum is explained in next section 5.2) for each patient was found to be 0.66 (p = 0.0001). The list of all patients COVID severity, Bispectrum strength, CONS (A pulmonary consolidation is a region of compressible lung tissue that has filled with fluid instead of air), and GGO values are shown in Table 12 (Appendix IV). The correlation and p values between variables of Table 12 (Appendix IV) are given in Table 6. The association between GGO and COVID severity is shown in Fig. 19, between GGO and Bispectrum strength is given in Fig. 20, and between COVID severity and Bispectrum strength is shown in Fig. 21. As seen the correlation between COVID severity and GGO values is quite high and similarly correlation between COVID severity and Bispectrum strength is also strong and further validates the COVID severity values.

Table 6 The correlation between GGO, CONS, COVID severity and Bispectrum
Full size table
Fig. 19
figure 19

Association between COVID severity and GGO values

Full size image
Fig. 20
figure 20

Association between Bispectrum and GGO values

Full size image
Fig. 21
figure 21

Association between Bispectrum and COVID Severity

Full size image

Performance evaluation

Diagnostics odds ratio

Diagnostic Odds Ratio (DOR) is used to discriminate subjects with a target disorder from subjects without it. DOR is calculated according to Eq. 8. DOR can take any value from 0 to infinity. A test with a more positive value means better test performance. A test with value 1 means it gives no information about the disease and with a value of less than 1 means it is in the wrong direction and predicts the opposite outcomes.

$$ \mathrm{DOR}=\frac{\mathrm{TP}/\mathrm{FN}}{\mathrm{FP}/\mathrm{TN}}=\frac{S_p\times {S}_e}{\left(1-{\mathrm{S}}_{\mathrm{p}}\right)\times \left(1-{\mathrm{S}}_{\mathrm{e}}\right)} $$
(8)

Where Se refers to the sensitivity and Sp refers to the specificity and is calculated using Eq. 9 and 10.

$$ \mathrm{Sensitivity}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}} $$
(9)
$$ \kern0.75em \mathrm{Specificity}=\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FP}} $$
(10)

where, TP, FP, TN, and FN represent true positive, false positive, true negative, false negative. The DOR values for all ML and TL methods are shown in Table 7. The variation of accuracy and DOR for three ML classifiers and five TL methods are shown in Fig. 22.

Table 7 Sensitivity, specificity with increasing order of DOR for the 3 ML and 5 TL systems
Full size table
Fig. 22
figure 22

Plot showing the relation between accuracy and DOR for 3 ML and 5 TL systems

Full size image

Receiver operating characteristics curve

Receiver Operating Characteristics curve shows the relationship between the false-positive rate (FPR) and the true-positive rate (TPR). The AUC validates our hypothesis. The ROC curves for 3 ML classifiers and 5 TL methods and 1 DL are given in Fig. 23. ROC curve is a plot between TPR (y-axis) and FPR (x-axis). The equation for TPR and FPR is given as Eq. 11 and 12.

$$ \mathrm{TPR}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}} $$
(11)
$$ \mathrm{FPR}=\frac{\mathrm{FP}}{\mathrm{FP}+\mathrm{TN}} $$
(12)
Fig. 23
figure 23

Plot showing ROC for 3 ML and 5 TL systems

Full size image

Performance evaluation metrics

Various performance evaluation metrics such as specificity, sensitivity, precision, recall, accuracy, F1-score, DOR, AUC and cohen kappa score of all ML and TL classifiers are presented in Table 8 in increasing order of accuracy.

Table 8 Performance evaluation metrics for all proposed AI methods
Full size table

Other statistical tests like Mann Whitney and paired -tests are described in Appendix V in Tables 13, 14, 15, 16 and 17.

Power analysis

We follow the standardized protocol for estimating the total samples needed for a certain threshold of the margin of error. The standardized protocol consisted of choosing the right parameters while applying the “power analysis” [63,64,65,66]. Adapting the margin of error (MoE) to be 3%, the confidence interval (CI) to be 97%, the resultant sample size (n) was computed using the following equation:

$$ \mathrm{n}=\left[{\left({\mathrm{z}}^{\ast}\right)}^2\times \left(\frac{\hat{\mathrm{p}}\left(1-\hat{\mathrm{p}}\right)}{{\mathrm{MoE}}^2}\right)\right] $$
(13)

where z∗ represents the z-score value (2.17) from the table of probabilities of the standard normal distribution for the desired CI, and p̂ represents the data proportion (705/(705 + 990) = 0.41). Plugging in the values, we obtain the number of samples 1265 (as a baseline). Since the total number of samples in the input cohort consisted of 1695 CT slices, we were 33.99% higher than the baseline requirements.

Discussion

This study used DL, TL, and ML-based methods for the classification of COVID-19 vs. Controls. The unique contribution of this study was to show three different strategies for COVID characterization of CT lung and the design of the COVID severity locator. Block imaging was implemented for the first time in a COVID framework and gave a unique probability map which ties with the existing studies. We further demonstrated the Bispectrum model and entropy models for COVID lung tissue characterization. All three methods showed consistent results while using 990 Control scans and 705 COVID scans.

The accuracy of proposed CNN was higher than other transfer learning-based models, this may be caused due to only 2 class classification problem. All the pre-trained models used in transfer learning were trained on a 1000 class ImageNet dataset and are winners of the ImageNet Large Scale Visual Recognition Challenge (ILSVRC) challenge. They are however designed with a huge number of hidden layers as shown in Table 2 and on training for only 2 class classification problems their accuracy is not highest. This may be due to a smaller number of output classes needing a smaller number of hidden layers and a smaller number of filters/nodes in these layers. In a similar way proposed CNN will not work well for a greater number of classes. The usage of pre-trained models leads to overfitting in which training accuracy starts showing 100% accuracy but testing accuracy is in range of 80–90%.

Pathophysiology pathway for ARDS due to of SAR-CoV-2

It is well established that SARS-CoV-2 uses the ACE2 receptor to grant cell access by binding to SPIKE protein (‘S’ protein) on the surface of cells [67,68,69] (see Fig. 24 showing the green color ACE2 receptor giving access to spike protein of SARS-CoV-2). Renin-Angiotensin-Aldosterone System” (RAAS) is the famous pathway where ACE2 and “angiotensin-converting enzyme 1” (ACE1) are homolog carboxypeptidase enzymes pathway [70] having different key functions. Note that ACE2 is well and widely expressed in (i) brain (as astrocytes) [71, 72], (ii) in heart (as myocardial cells) [70], (iii) lungs (as type 2 pneumocytes), and (iv) enterocytes. This leads to extra-pulmonary complications. Figure 24 shows a Hypoxia pathway (reduction in oxygen) showing the reduction of ACE2 levels once the SARS-CoV-2 enters the lung parenchyma cells. This causes a series of changes leading to “acute respiratory distress syndrome” (ARDS) [73]. This includes (a) accumulation of exaggerated neutrophil, (b) enhancement of vascular permeability, and finally, (c) the creation of diffuse alveolar and interstitial exudates. Due to oxygen and carbon dioxide mismatch in respiratory syndrome (ARDS), there is a severe abnormality in the blood-gas composition leading to low blood oxygen levels [74, 75]. This ultimately leads to myocardial ischemia and heart injury [76, 77]. Our results on COVID patients show clear damage to CT lungs, especially in inferior lobes, which is very consistent with the pathophysiological phenomenon of SARS-CoV-2.

Fig. 24.
figure 24

ARDS phenomenon due to SAR-CoV-2.

Full size image

Comparison of COVID lung severity location with other studies

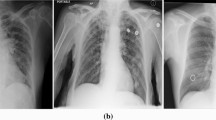
A very curial point to note here is that our system characterizes the lung region based on COVID severity. This characterization shows that all three classifiers (RF, DT, and k-NN) used in Block imaging have a more or less the same behavior in the sense that COVID severity is highest in the inferior lobe of the right lung and close to the base of the lung (near the diaphragm). This was well noted pathologically by several studies as well [2,3,4,5,6,7,8]. The images from existing research are shown in Fig. 25. The top row shows the COVID infected lung pointing out the COVID severity by black arrows ((a) Pan et al. [2] showing COVID severity more in the lower lung regions, (b) Wang et al. [16] similarly showing the severity of infection in lower lobes of lungs, (c) Tian et al. [5] chest CT also showing the point of infection near the lower part of the left lung). The middle row shows the chest X-ray scans of the Control and COVID patients ((d) Elasnaoui & Chawki [78] showing normal lung X-Ray, (e) Elasnaoui & Chawki [78] showing COVID lung X-Ray, (f) Aigner et al. [7] showing COVID CXR). The bottom image shows the color-coding of the probability map using Block imaging. The RED color is the highest COVID severity which matches the top row COVID severity locations (which is part of the inferior lobes, as shown in the anatomy as well).

Fig. 25
figure 25

a Pan et al. [2] showing COVID severity more in the lower lung regions, b Wang et al. [16] similarly showing the severity of infection in lower lobes of lungs, c Tian et al. [5] chest CT also shows the point of infection near the lower part of the left lung, d Elasnaoui & Chawki [78] showing normal lung X-Ray, e Elasnaoui & Chawki [78] showing COVID lung X-Ray, f Aigner et al. [7] showing COVID CXR, g image showing the anatomy of lungs, h original grayscale image from this study’s dataset with a white arrow pointing severity of infection at the bottom part of the right lung, i Block imaging showing most severity of infection in the right lower lobe of lung in RED color

Full size image

Benchmarking against previous studies

Table 9 presents the benchmarking table that compares five main studies for lung tissue classification (R1 to R5). Six different attributes are used for the comparison (shown from C1 to C6). This includes the year in which it was published (column 1), the technique used (such as ML vs. DL or TL in column 2), the data size adapted in the protocol (in column 3), classification accuracy (in column 4), COVID severity (column 5) and ability to characterize the lung tissue (in column 6). Note that the unique contribution of our study comes in the way we compute the COVID severity by designing the color map superimposed on the grayscale CT lung slice. Further, we developed three different kinds of strategies for tissue characterization for COVID lungs based on (a) Block imaging strategy, (b) Bispectrum using higher-order spectra, and (c) entropy analysis. Another important accomplishment of our work is the achievement of higher accuracy even with conventional classifiers like Random Forest, which is in the range close to 100% with AUC close to 1.0 (p < 0.0001), as shown in the box (R6, C4).

Table 9 Benchmarking of the proposed CADx study against the existing work in COVID classification and characterization
Full size table

Most of the methods which have been recently published use the transfer-learning paradigm, where the initial weights are taken from the natural images or animal data called the “ImageNet” dataset [79]. Three of the five techniques use “DenseNet” based on TL having accuracies in the low 80% or high 80% range (see row numbers: R2, R3, R4). Two of the five techniques used “ResNet-18” and “ResNet-50” (R1 and R5) having the accuracy in low 90% and one in a high 90% range. Even though we also use DL and TL, however, we do adopt a low number of features with the usage of the feature selection paradigm for ML methods.

Special note on transfer learning models

VGG16 is a pre-trained model with 13 convolution layers and 3 dense layers which gives the name VGG16 due to 13 + 3 = 16 main layers in the model. It gives the encouraging results on the ImageNet dataset and is thus use widely adapted for transfer learning in different image classification problems. The size of the weights file of VGG16 is however huge and thus to solve this problem MobileNet was introduced for deployment on mobile devices with reduced storage using width multiplier and resolution multiplier having almost a similar accuracy as VGG16. As seen from DenseNet architectures, the number of batch normalization layers gives the corresponding name of the DenseNet model. For each layer, the feature-maps of all preceding layers were used as inputs, and its own feature-maps were used as inputs into all subsequent layers. DenseNets have several advantages: they solve the vanishing-gradient problem, strengthen feature propagation, encourage feature reuse, and substantially reduce the number of parameters. The pre-trained models, however, are designed for 1000 class problems thus to design a CNN for only 2 class COVID classification problems a simpler model was needed with only 7 layers as shown in Fig. 6 and was found to give better results than pre-trained models.

Strengths, weakness, and extensions

Strengths

In the first part of the study, we compared one type of deep learning and 5 transfer learning-based methods of COVID classification and showed they performed with high accuracy using K10 protocol. ML classifiers were also experimented and they also showed comparable accuracy with DL models. The next part of the study demonstrated how the division of lung into blocks and carrying classification of individual blocks can help to identify the most severely affected area of the lung infected in COVID patients. This matches other research work which also tells that lower lung segments are most affected by COVID. Bispectrum after Radon transform of images also shows much higher values for COVID images, thus supporting the hypothesis of more visible areas of congestion in diseased lungs. Finally, block-wise entropy of lungs also showed more random texture in lower blocks of lungs of COVID as compared to Control patients. These three methods form a strong basis for characterizing the severity of COVID infection in affected patients. The COVID tissue characterization was validated against the ground glass opacity (GGO) values of CT scans and it was found COVID severity using block imaging showed high correlation with GGO values. Similarly, Bispectrum also showed high correlation with GGO values, thereby validating the characterization systems. Validation of classification results was also done using the Diagnostics Odds Ratio (DOR) and Receiver Operating Characteristics (ROC) curve.

Limitations

Although we used a limited size of the cohort it was demonstrated that 9 AI classification systems and 3 characterization systems gave a high performance in terms of accuracy and correlation with GGO values, ensuring that the system is reliable and foolproof. It is not unusual to see lesser cohort size in standardized journals [80, 81] and that uses AI-based technologies first time on newly acquired data sets [82,83,84,85,86]. Despite the novelty in CL lung characterization and classification paradigms on the Italian database, a more diversified CT lung dataset can be collected retrospectively from other parts of the world such as Asia, Europe, the Middle East, and South America for further validation of our models.

Extensions

Further, we can extend our models from ML to DL for classification and characterization of “mild COVID lung disease” vs. “other viral pneumonia lung disease”. The study can be extended for larger and diversified cohorts. We intend to bring viral pneumonia cases over time and for better multi-class ML models [87, 88]. More automated CT lung segmentation tools can be tried [11, 89, 90] as COVID data evolves and readily get available. Further, systems can undergo variability analysis in segmentation [91] and imaging different types of scanners [92]. To save time, transfer learning-based approaches can be appropriately tried in a big data framework [93]. Lastly, more sophisticated cross-modality validation can be conducted between PET and CT using registration algorithms [11, 94,95,96].

Conclusion

This study presented a CADx system that consisted of a two-stage system: (a) lung segmentation and (b) classification. The classification system consisted of one proposed CNN, five kinds of transfer learning methods and three different kinds of soft classifiers such as Random Forest, Decision Tree, and ANN. Further, the system also presented three kinds of lung tissue characterization systems such as Block imaging, Bispectrum analysis, and entropy analysis. Our performance evaluation criteria used diagnosis odds ratio, receiver operating characteristics, and statistical tests of the CADx system. The best performing soft classifier was proposed CNN and Random Forest having an accuracy of 99.41 ± 5.12% and AUC of 0.991 p < 0.0001 and 99.41 ± 0.62% and AUC of 0.988 p < 0.0001. The characterization system demonstrated the color-coded probability maps having the highest accuracy in the inferior lobes of the COVID lungs. Further, all three kinds of tissue characterization system gave consistent results on COVID severity locations. This is a pilot study and more aggressive data collection must be followed to further validate the system design. This pilot study was unique in its ability to perform best with limited data size and limited classes. We anticipate extending this system to multiple classes consisting of Control, mild COVID, and other viral pneumonia.