Introduction

The increasing amount of medical data stored in data sets is creating an urgent need for efficient algorithms for information retrieval. The bigger the databases are, the greater the chance that even a small relation or unobserved information at first sight will be found [24]. The types of data stored include not only plain text but also images, sounds and other types of digitalized information. While sophisticated methods for full-text retrieval have been created, the efficient retrieval of other types of data such as image, voice or video data remains a still open problem.

In the article, we present a method for fuzzy medical image retrieval (FMIR), concretely in mammography. In the medical area, there are some proposed approaches for image retrieval. Such as in [11] the authors proposed to use Wavelet transforms in a one and two-level decomposition for finding the normal regions and the regions containing the lesion, then they proposed using the coefficients obtained using the wavelet decomposition in a support vector machine classifier with a linear kernel. A very interesting approach is described in [50], the method enables the localization of the pathology area in medical images. The proposed approach utilizes the linguistic theory of pattern classification. The interpretation is built on cognitive processes, which is based on the human psychological processes of the understanding of the registered patterns in images. Our main inspiration was taken from information retrieval, document signatures, and NCD, the known approach is modified with the usage of vector quantization.

The article organisation is as follows: the workflow of the proposed FMIR method with respect to the necessity of the explanation of the theoretical principles of the proposed method. In the first part of this article, the theoretical principles of the methods used can be found. “Vector quantization” describes VQ, the following “TF-IDF” introduces TF-IDF. The next section explains signature files and the connection to fuzzy signatures and their organisation in computer memory (“Brief description of signature files” and “Fuzzy signatures”). The proposed method is compared to NCD, and it is defined in “Normalized compression distance”. The following “Fuzzy medical image retrieval” and “Experiments” describe the proposed FMIR method and the setup of the experiments. The results of FMIR method and NCD are summarized in “Results”. The last “Conclusion” sums up and concludes the experiment results.

Related work

Primarily, there are two ways how to search for similar images: querying the images is based on the keyword TBIR (Text-Base Image Retrieval) [45, 62] and based on the content CBIR (Content-Base Image retrieval) [13, 74].

The TBIR system can return the images with content that are not related to the request of querying since the nature of the keywords is independent of the content of the images. To overcome this problem, the CBIR system extracts the visual attributes of the images which are needed to query and then compare with the visual attributes of the other images. However, if the method of comparing the similarity of the content is ineffective, the results of querying put out the images with content which are not related to the requested query.

The similarity assessment method of images based on vector quantization, TF-IDF (Term Frequency–inverse Document Frequency), fuzzy signatures and the method of querying images based on the fuzzy S-tree (FS-tree), is built in the presented article. Vector quantization is used as a tool for the transformation of an image to a fuzzy signature and for creating the codebook. It was used in the past several times. A comparison of the vector quantization codebook was used for image retrieval in [58], Teng [67] uses vector quantization from image indexing and retrieval with the preservation of pixel position and Rahman et al. [55] uses vector quantization in fuzzy feature space for biomedical image retrieval. The proposed method is compared with the method, where Normalized Compression Distance (NCD) for similarity assessment is used.

NCD is based on Kolmogorov complexity. Calculation of Kolmogorov complexity requires high computing power. That is why in real applications it is approximated using compression algorithms [39]. The NCD has been used in text retrieval [21], text clustering, plagiarism detection [65], music clustering [21] and [49], music style modelling [17], automatic construction of the phylogeny tree based on whole mitochondrial genomes [42], the automatic construction of language trees [2] and [41], and the automatic evaluation of machine translations [16]. NCD has also been successfully applied in challenging areas, for example, spam detection [54] or EEG data for simple cognitive tasks [3]. The disadvantage of a method with NCD is that it is not able to capture the areas of interest in the image, which can help a physician. The distance for the assessment of the similarity of images is also proposed, which is used for the creation of the list of the similar images. This list is then utilized to determine if a medical finding is malignant or benign. This knowledge is obtained from the comparison of known cases and can be used for classification of the medical cases.

In the context of our search for new ways of looking at signature methods, we tried to apply a fuzzy approach to signature construction and manipulation. The result is the definition of fuzzy signatures which is presented. The side idea of the paper, which is going to be elaborated is to use fuzzy signatures to interface the TBIR and the CBIR.

The requirement for the widening of the palette of methods for image retrieval in our case is the growing usage of imaging methods in the medical area such as X-ray, computed tomography (CT), magnetic resonance imaging (MRI), ultrasonography (USG), positron emission tomography (PET) or single-photon emission computed tomography (SPECT) [29]. e.g. during the preoperative examination, during the surgery or the postoperative period, the amount of the picture, which needs to be assessed and compared is still rising [28, 70]. Nowadays, it is done using human power and requires a lot of time. One aspect of the power of the amount of images, which are stored in hospitals and research medical centers, is still neglected. In [73], the application of fuzzy signature for medical data is proposed. As fuzzy reasoning is used, the proposed method can be considered as bioinspired in a specific point of view.

Vector quantization (VQ) is a classical quantization technique which allows for the modeling of probability density functions through the distribution of prototype vectors. It was originally used for data compression. It works by dividing a large set of points (vectors) into groups with approximately the same number of points closest to them. Each group is represented by its centroid point, as in k-means or some other clustering algorithms. It has been used for image compression, CBIR, and image indexing for many years in many fields. In [1] Arya and Mount presented and compared three algorithms for nearest neighbor searching in high dimensions, within the framework of vector quantization. Two of the algorithms provide drastic reductions in complexity with a negligible deterioration in performance. The papers [9, 10] presented VQ for image processing. The authors presented a multitude of various approaches for codebook construction and its application in the field of image processing. Park in [51] proposed a new block-transform-based image compression scheme by combining vector quantization (VQ) and two transformations, discrete cosine transform (DCT) and vector-embedded Karhunen-Loève transform (VEKLT) [66]. The author’s proposed method performs better in peak signal-to-noise ratio if the bits per pixel (bpp) increase because the ratio of blocks which are processed by VQ and VEKLT increases. The visual quality of the proposed method is better than that of JPEG in high detail. The authors Huang and Harris in [25] investigated a performance comparison of several often-used VQ codebook generation algorithms. The discussed algorithms include the Linde-Buzo-Gray (LBG) binary splitting algorithm, the pairwise nearest neighbor algorithm, the simulated annealing algorithm, and the fuzzy c-means clustering analysis algorithm, and the new directed-search binary splitting method, which reduces the complexity of the LBG binary.

In [43], the authors presented an image indexing and retrieval scheme based on VQ. The results obtained by the authors show that it has a higher retrieval performance than the basic colour histogram based approach. In addition, it is computationally more efficient.

The increasing amount of digitally produced images in various areas, for example journalism, medicine, is requiring fast and effective ways of image accessing. The need for a fast and effective solution is growing. Deselaers et al. [15] discussed a large variety of features for image retrieval and a setup of five freely available databases. From the experiments conducted it can be deduced, which features perform well on which kind of task and which do not.

Vector quantization

Vector quantization has been used for image compression for many years. In this section, we will briefly review the basic concepts of VQ image compression. In most image compression techniques, the actual quantization or coding is done on scalars (e.g. on individual real value samples of waveforms or pixels of images). Transform coding does it by first taking the block transformation to a block of pixels and then individually coding the transform coefficients. Predictive coding does it by quantizing an error term formed as the difference between the new sample and a prediction of the new sample based on pasted coded outputs [67].

A fundamental result of Shannon’s rate-distortion theory [61], the branch of information theory devoted to data compression, is that a better performance can always be achieved by coding vectors (a group of values) instead of scalar (individual value). Thus, vector quantization can successfully be used for image and audio compression. A vector quantizer can be defined as a mapping Q of k-dimensional vector space \(\mathbb {R}^{k}\) into a finite subset \(\mathcal {C}\) of \(\mathbb {R}^{k}\), that is \(Q : \mathbb {R}^{k} \to C\), where \(\mathcal {C} = \{c_{1}, c_{2}, \ldots , c_{n}\}\). \(\mathcal {C}\) is the set of reproduction vectors and is called a codebook. \(|\mathcal {C}| = n\) is the number of vectors in \(\mathcal {C}\). At the encoder, each data vector x belonging to \(\mathbb {R}^{k}\) is matched or approximated with a codeword in the codebook and the address or index of that codeword is transmitted instead of the data vector itself. To find the best match codeword for a data vector, we can use Euclidean or Manhattan distance.

Vector quantization can be used for image transformation to fuzzy vector.

TF-IDF

TF-IDF [40], is a numerical statistic that is meant to reflect how important a word, n-gram or other term is to a document in a set of documents. TF-IDF is a weighting factor in text information retrieval and text mining applications. TF-IDF assigns a higher value of weight to terms which occurs rarely in the collection of documents. The terms with a higher occurrence frequency are evaluated with this lower weight. This means that these terms are less important in the documents.

TF-IDF is the product of two statistics values, TF and IDF. TF (Term Frequency) is a value that represents how often a particular term appears in a concrete document. The more frequent the term is in the document, the more important the term in the document is. The common terms in the collection, that appear in many documents, have the highest frequency. For example, the word ``patient” is frequently mentioned in medical documents, and its TF would be very high. In other documents, this word can rarely be found and its TF is low. Therefore, we need to control the importance of the word. This situation is adjusted by IDF (Inverse Document Frequency). DF (Document Frequency) is obtained by dividing the total number of documents by the number of documents containing the term. IDF is the inverse value of DF. TF-IDF is widely used in many text data mining and data analysis applications [40].

Brief description of signature files

In [34], an application of the signature for the more efficient processing of range queries is studied. This approach puts the signature into multi-dimensional data structures like R-tree [23] or UB-tree [56] but original functionalities are preserved, i.e. the range query algorithm for the general range query.

At first, we would like to introduce the basic principles of general signature methods. For example the details can be found in [4, 18, 30, 76]. As was mentioned, we used the inspiration in information and image retrieval [36, 37, 48]. For the usage of signatures for images, we inspired ourselves in the signatures of text documents, so the principle is going to be described, for easier understanding, on a text – document example.

The information retrieval methods are able to separate a finite set of all documents D={D 1,D 2,…,D k } into two subsets – a set of relevant documents and the rest of the documents. The extracted documents in the subset of relevant documents are determined for a given query Q. A certain required amount of work is needed before a query can be evaluated. During this work, auxiliary data structures are created. These structures are used for later evaluation of any given query. In methods where signatures are utilised, signatures are considered as auxiliary structures.

In general, a signature is a bit string s 1 s 2…s n , of a fixed length n. Each document has its own signature and is used for query evaluation. Both signatures, signature S i of a document D i and query signature S Q , have a length of n. Document D i is relevant only if its signature S i contains ones in all positions in which ones are encountered in the query signature S Q .

We can divide the ways of creating signatures into two main principles: superimposed coding and concatenation. In our article, we use superimposed coding and we will discuss this principle in more detail.

Every signature with superimposed coding is created in the following way. In the beginning, the bit string of signature S i = s 1 s 2…s n contains zeros in all positions. A document consists of a finite set of distinct words {w 1,w 2,…,w l }. For each word w i belongs m bit positions in the signature S i . These bit word positions should not overlap and should be distributed evenly throughout the full length of the signature. If the bit string contains zeros in these positions, they are replaced with ones. The word bit position is usually chosen as a result of a hash function which takes the word w j as an argument. The result of this method is the same as if a signature were created separately for each word w j . Also, this signature would contain up to m ones. The signature of the whole document is the result of superimposing all individual signatures \(S_{w_{1}}, S_{w_{2}}, \dots , S_{w_{l}}\). An example of signature superimposed coding is described in Algorithm 1.

figure a

Fuzzy signatures

Another issue to be resolved is the way fuzzy signatures are organized in the signature file. The simplest way would be to store the fuzzy signatures in sequential order. This method is not efficient if the time required for query evaluation is concerned. That is why we have modified the data structure called S-tree, which is traditionally used to store ordinary signatures. In the next section, we will present the modification which enables using this data structure to store fuzzy signatures.

In this chapter, we describe persistent data structures for searching efficiently, i.e., fast, for images similar to a query image within a large database. Mapping images to fuzzy signature is an elegant way how to solve the problem. Since we use fuzzy signatures to represent images we address the efficiency issue by proposing the use of an enhanced fuzzy signature tree (FS-tree) [52, 53, 63, 64].

Fuzzy signatures are hierarchical representations of data structuring into vectors of fuzzy values. A fuzzy signature is defined as a special multidimensional fuzzy data structure, which is a generalization of vector valued fuzzy sets. Vector valued fuzzy sets are special cases of L-fuzzy sets which were introduced in [19]. Fuzzy signatures are studied in [33, 69].

The weighted aggregation concept is proposed [46] to provide additional expert knowledge to the fuzzy signature structure by introducing the weighted relevance of each branch to its higher branches of the fuzzy signature structure. In [32], vector valued fuzzy sets are introduced as the generalization of the original concept of fuzzy sets [31, 75].

Definition 1

The fuzzy signature F is a vector f 1 f 2…f n , where f i ∈〈0;1〉 ∀i=1,2,…,n.

Provided that we have created fuzzy signatures for all documents in the set D and that we have the fuzzy signature F Q of the query Q, we can use the operation of conjunction to find the relevant documents. The operation is defined in the same way as in fuzzy logic.

Definition 2

The conjunction of fuzzy signatures F i and F j is the fuzzy signature

$$ F_{i} \otimes F_{j} = (f_{i_{1}} \otimes f_{j_{1}}) (f_{i_{2}} \otimes f_{j_{2}}) {\ldots} (f_{i_{n}} \otimes f_{j_{n}}). $$
(1)

The operation ⊗ could be defined as one of the possible functions of the family of the functions, which are called the operation of triangular norm (t-norm) see [20]. The example of the possible interpretation of the t-norm function is provided in Table 1.

Table 1 Example of possible interpretation of t-norms and t-conorms functions
Full size table

In order to find all documents relevant to the given query Q we have to find all documents D i which satisfy the formula F i ⊗F Q = F Q . This means that for a document to be relevant to the query, all the elements of its signature must be equal to or greater than all the corresponding elements in the query signature.

Definition 3

The disjunction of fuzzy signatures F i and F j is the fuzzy signature

$$ F_{i} \oplus F_{j} = (f_{i_{1}} \oplus f_{j_{1}}) (f_{i_{2}} \oplus f_{j_{2}}) {\ldots} (f_{i_{n}} \oplus f_{j_{n}}). $$
(2)

The operation ⊕ could also be chosen from the set of the functions, which are in this case called triangular co-norm – t-conorm or known as the s-norm [20] (Table 1).

These definitions of logical operations with fuzzy signatures reflect the t-norm and s-norm [20], the common definitions of logical operations in fuzzy logic.

We have described the method of evaluating a query by examining the fuzzy signatures of individual documents and the signature of the query itself, but we have not discussed how fuzzy signatures are constructed. We assume that the elements f i of the string F are degrees of membership of the sets M i . That is why using fuzzy signatures depend on determining the sets M i .

It is possible to construct these sets in the following way, so let the set A be the set of all distinct words that can appear in all the documents. Let δ be the distance on the set A. We can apply clustering methods to the set A using the distance δ. It will give a finite number of clusters which will become the sets M i . For each word w in the document D i , the degrees of membership in the sets \(M_{1},M_{2},\dots , M_{n}\) can be estimated using the distance δ and used as the elements of the fuzzy signature of this word. The fuzzy signature F i of the whole document D i is the disjunction of the fuzzy signatures of all the words.

$$ F_{i}=F_{w_{i1}} \oplus F_{w_{i2}} \oplus {\cdots} \oplus F_{w_{il}}. $$
(3)

We could use the set of all distinct words in the corpus of a natural language as the set A. We could try to apply some of the metrics used in linguistics which reflect relationships between words in the corpus. However, this concept of fuzzy signature construction has not yet been implemented.

Fuzzy S-tree

Deppisch, in [14] proposed a B-tree like structure to facilitate fast access to the records (which are signatures) in a signature file. The leaf of an S-tree consists of similar (i.e. with small distance) signatures along with the document identifiers. The OR-ing of these k document signatures forms the key of an entry in an upper level node, which serves as a directory for the leaves. Higher-level nodes are constructed recursively, in the same way. Like a B-tree, the S-tree is kept balanced: when a leaf node overflows, it is split into two groups of similar signatures; the father node is changed appropriately to reflect the new situation. Splits may propagate upwards.

S-tree is a balanced tree which uses similar principles as the well-known B-tree or its variation, the B +-tree. S-tree is a data structure which allows searching for, inserting and removing signatures [14, 47].

The modified S-tree [5] adds to the S-tree a third table (the count table) that stores, for each internal node, the number of leaves in its left subtree. The addition of the count table to the modified S-tree allows more efficient searches. In a modified S-tree, we can look up a given code without traversing the complete sequence, using the count values to jump forward in the sequence: if we want to go to the second child of a node, instead of traversing the complete first child we use the count to jump directly to the second child. It makes navigation faster but the space requirements are significantly higher.

The compact S-tree [6] is another variant of the S-tree that uses a single table (the linear-tree table) to represent the same information stored in the three tables of the modified S-tree. The compact S-tree is built from a bintree traversing the tree in preorder. For each internal node found, the number of leaves in its left subtree is added to the table. For each leaf node found, its color is added to the table. The final result is a sequence that contains a single symbol per node of the bintree: the number of leaves covered by each internal node and the color of each leaf node.

The major advantage of the S-tree structure is the reduction of the number of signatures which must be searched for during the evaluation of a query. In an ideal case, this number would be proportional to the height of the tree. However, this situation is very unlikely as we will explain in the section devoted to the splitting of tree pages.

FS-tree was introduced in [52, 63]. FS-tree is fuzzification of S-Tree [14, 68].

Fuzzy distance δ

$$ \delta (S,S^{\prime}) = \gamma (S\oplus S^{\prime}) - \gamma (S~\otimes S^{\prime}), $$
(4)

where S and \(S^{\prime }\) are signatures of the page and of the inserted document, and

$$ \gamma(S) = \sum\limits_{i=1}^{L}s_{i} $$
(5)

is the weight of the signature S, where L is the length of the signatures or instead of the weight function one of many aggregation functions could be used [20].

Normalized compression distance

NCD is a mathematical way of measuring the similarity of two documents D x and D y . The measuring of similarity is realized with the help of compression where repeating parts are suppressed by compression. NCD may be used for the comparison of different objects, such as images, music, texts or gene sequences. NCD has requirements to a compressor. The compressor meets the condition

$$ C(D_{x}D_{x}) = C(D_{x}), $$
(6)

within logarithmic bounds [59]. NCD can be used for the detection of plagiarism and visual data extraction [7, 71]. The resulting rate of the probability distance between two documents D x and D y is calculated by the following formula

$$ NCD\left( D_{x},D_{y}\right)=\frac{C\left( D_{x}D_{y}\right)-min\left( C\left( D_{x}\right),C\left( D_{y}\right)\right)}{max\left( C\left( D_{x}),C(D_{y}\right)\right)}, $$
(7)

where

  • C(D x ) is the length (size) of compression of document D x ,

  • C(D x D y ) is the length (size) of compression concatenation of documents D x and D y ,

  • m i n(C(D x ),C(D y )) is the minimum of values \(C\left (D_{x}\right )\) and \(C\left (D_{y}\right )\),

  • m a x(C(D x ),C(D y )) is the maximum of values \(C\left (D_{x}\right )\) and \(C\left (D_{y}\right )\).

The NCD value is in the interval 0≤N C D(D x ,D y )≤1 + 𝜖. If N C D(D x ,D y )=0, then documents D x and D y are equal. They have the highest difference when the result value of N C D(D x ,D y )=1 + 𝜖. The constant 𝜖 describes the inefficiency of the used compressor. The NCD is not a metric. NCD approximates the computable Normalized Information Distance [72] with difficulty. The computation of the NCD is a very efficient way of measuring a distance between two documents because we do not need to create the output of the compression algorithm.

Fuzzy medical image retrieval

The fuzzy medical image retrieval (FMIR) method is a novel method for medical image similarity assessment and content retrieval using VQ and fuzzy signatures in conjunction with the FS-tree. The workflow of the whole method is depicted in Fig. 1. The method can be divided into the following main parts/tasks:

  • Vector Quantization – in this block a codebook is created. The code book is used to convert medical images into vectors.

  • Creation of Fuzzy Signatures – in this step the images vectors are converted into fuzzy vector. Each image is represented as a single fuzzy vector – signature.

  • FS-tree – a data structure, which organizes fuzzy vectors – signatures in the tree form and allows to find similar fuzzy vectors to a given query.

Fig. 1
figure 1

The workflow diagram of FMIR

Full size image

The presented FMIR method is compared with the method using NCD, with utilized Bzip2 compression algorithm [60], instead of fuzzy signatures and FS-tree (Fig. 1). In the workflow, it can be seen that for the initialization and running phase the algorithm parts are the same. Both phases share the same codebook.

For the evaluation purposes, the experiments collection of medical images is divided into two groups of images. The first group is the training group of images \(\mathcal {X}=\{I_{1},\dots ,I_{i}\}\), (where I i is a medical image), which is used for creating the codebook \(\mathcal {C}=\{c_{1},\dots ,c_{n}\}\) by VQ and creating the FS-tree. The second group of images \(\mathcal {Y}\), is used for the evaluation of the proposed method. The second group of images can be newly obtained images or images from different patients.

In the proposed method, an image I is transformed into the series of blocks \(\mathcal {B}\) of s×s pixels using function \(f:I\to \{b_{1},\dots ,b_{m}\}\), where m is the number of obtained blocks in I. Each block b of I is represented as a vector \(b=(p_{11}, p_{12}, {\dots } , p_{1s}, p_{21}, \dots , p_{ss})\), where p i j ∈<0;1>, is the grayscaled value of a pixel on i-th row and j-th column. These blocks are used in both experiments – FMIR and NCD.

As was mentioned in the previous paragraph, the \(\mathcal {X}\) is transformed using the function f into a series of blocks \(\mathcal {B}\). These blocks are used to create the codebook \(\mathcal {C}\). The initial set of \(\mathcal {B}\) is used to construct the desired \(\mathcal {C}\) with the size n. To construct the \(\mathcal {C}\) we utilized k-Means clustering (Algorithm 2) algorithm with n clusters [44]. The output of the Algorithm 2 are the centroids of the n clusters. These centroids represent the codes \(c_{1},\dots ,c_{n}\) in the \(\mathcal {C}\). We are not limited to using k-Means, we can choose many ways of how to construct the codebook.

figure b

The obtained codebook \(\mathcal {C}\) is used to convert database images \(\mathcal {X}\) and query images \(\mathcal {Y}=\{I_{1},\dots ,I_{m}\}\) into fuzzy signatures. Using the function \(g(\{b_{1},\dots ,b_{m}\},\mathcal {C})\to \mathbb {R}^{n}\), where the function output is the fuzzy signature. This function maps each block b to a codec from the codebook \(\mathcal {C}\) and creates the fuzzy signature. We choose the code c with the shortest distance between block b and code c. The function g calculates the membership value for each code. The size of the vector is the same. In our proposed method TF-IDF (see “TF-IDF” for more details) is utilized. The TF-IDF suppresses the membership value of blocks that occur very frequently in the images from the database. For example, it can be blocks of the I, which consists only of black color or other frequent blocks in I. This kind of block has no significant information. To calculate TF-IDF, we need occurrences of codes in the codebook, These counts are stored in vector G. The individual steps are described in Algorithm 3. We are not limited to use the TF-IDF, many other ways of how to set the membership degree of the code can be chosen, i.e. Okapi BM25 [57].

The fuzzy signatures, which are obtained from the set of images \(\mathcal {X}\), are used to create the FS-tree. This tree-based data structure allows us to find similar fuzzy signatures in a short time. Similar images have similar fuzzy signatures and these fuzzy signatures are stored in close or the same nodes of the FS-tree.

The query images from \(\mathcal {Y}\) are processed in the same way as images from \(\mathcal {X}\). The function f converts the query image into blocks and assigns the code c to each block. Afterwards, the function g creates the fuzzy signature. As a result of a query to the FS-tree, the tree returns a list of similar medical images. The results are sorted from the shortest distance to longest. The shorter indicates the higher similarity between the query image and the resulting image.

figure c

Experiments

The main goal of these experiments is to assess if, using the proposed method, it is possible to find medical images with a high similarity to the given query image. And the next aim is to assess the nature of the query image – if it is of a benign or malign nature. This is done using the list of similar images and the number of benign and malign nature images on the list of a predefined length. In the first step, we created a codebook \(\mathcal {C}\) using VQ and k-Means clustering algorithm. The codebook was created using 1000 radiographs from the data set (500 benign and 500 cancer images) for both, CC and MLO views. The selected images belong to different patients and are of the same type. We set the size of the block to 8×8 pixels. This block size contains enough information to construct fuzzy signature that characterizes an image. In our experiment, we created a codebook \(\mathcal {C}\) of size 200 codes. The similarity of fuzzy signatures was measured using fuzzy distance, for more details see “Fuzzy signatures”. Some combination of t–norms and t–conorms was tested to define the fuzzy distance, so experiments taking into the account the different ways of fuzzy distance definition, are included. The discussion on whether it is possible to provide repeatability is also included.

Data description

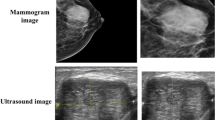
To test our method, we first decided to use QIN Breast DCE-MRI dataset [8, 26]. This collection of breast dynamic contrast-enhanced (DCE) MRI data contains images from a longitudinal study to assess breast cancer response to neoadjuvant chemotherapy [27]. This collection of MRI images is freely available to use. The value of this collection is to provide clinical imaging data for the development and validation of quantitative imaging methods for the assessment of breast cancer response to treatment. The images from this database show the big area of the body. The usage of this type of images was limited, because parts of the image with other parts of the human body than the area of interest, influenced the results too much.

So the other database – Image Retrieval in Medical Applications (IRMA) Version of Digital Database for Screening Mammography (DDSM) LJPEG Data, with image in PNG format, which was found as very useful, was used [38]. The IRMA DDSM database consists of 9.852 radiographs (X-ray images) of breast, where normal, cancer and benign cases are included [11]. The normal cases, from our point of view, are not interesting, because they can be assessed very easily, the interesting problem is to assess if the radiographs with some problematic areas are cancerous or benign. Overall, we used 4000 radiographs.

The size of the radiographs varies from 1024×300 pixels to 1024×800 pixels. However, for our application the size of the images is not significant and the rotation of the image is also not significant. The database is composed of two types of views of the breast, of craniocaudal (CC) and mediolateral (MLO) views [12]. For our experiments, the groups were separated and the method was proven for both groups separately.

Description of used computational equipment

The experiments were run on a computer with two Intel Xeon Processor E5-2680 v2 (25M Cache, 2.80 GHz, 20 threads) CPUs installed with 768 GB of main memory. The application is capable of using the maximal number threads of both CPUs. Most parts of the suggested method are parallelized. The parallelization helps to reduce the required time which is needed to create the codebook, code input images, compute fuzzy signatures, and to evaluate the query. All necessary information is stored, the fuzzy signature tree and TF-IDF information, in the computer memory, which helps to minimize the time of the query evaluation. The most complex part of the suggested method is the codebook creation. This step has to be done only once, then the codebook is loaded and used. The query evaluation is processed very quickly.

Results

In this section, the obtained results with discussion are mentioned. To evaluate FRIM (“Fuzzy medical image retrieval”) the data set described in “Data description” was used. The proposed FMIR method is compared to the method based on compression-based distance - NCD (Fig. 1). The approach with NCD takes into account the position of each block in the radiography image.

Results can be divided into two parts – the finding of similar pictures and picture classification.

Within the task of the finding of similar pictures, three picture sets are presented for illustration. The first two using FMIR – variant with Bold product & sum and Minimum & Maximum used for defining the fuzzy distance, the third one using the NCD. All images are rotated to the same side, because it could be hard for readers to assess the similarity of differently rotated images.

The assessment of classification efficiency is done for 2000 images – 1000 of the craniocaudal (CC) view (500 benign and 500 malign) images and 1000 of the mediolateral (MLO) view (500 benign and 500 malign) images, to be able to assess the repeatability. Experiments are performed in this way: first of all the query image is chosen (randomly). For the query image, the most similar pictures are found and presented as pictures. Then the classification, which is used to find the nature (malignity or benignity) of the query image was done. For every image in query, the list of the most similar images is written. The list is cut to 10, 20, 30 and 50 of the most similar images. Using this, we want to find the appropriate cut off of the list to be able to determine the membership in one of the classes of the query image - whether it is the malign or benign class. For every cut, the amount of the pictures of the benign and malign class are counted. The class (nature), which is bigger is significant for the assessment of the query image nature. If the ration of benign and malign pictures on the list is equal, the image is assessed as malign, because in breast cancer, it is more dangerous to determine an ill patient as a healthy patient, it means, that the smaller the false negativity is, the better. The fuzzy distance was defined in six ways, so experiments were repeated six times. All combinations of t–norms and t–conorms, which were used for the definition of the fuzzy distance, can be seen in Table 1. Only the combination listed in rows were used, but many other combinations can be defined and used.

For the classification part, one of the main tasks is to declare the repeatability for every variant of fuzzy distance definition and for every image class (benign and malign) 500 experiments were done, followed by the performing of the statistical assessment. As it is necessary to be able to confidently identify both image classes – benign and malign, the results are presented separately for benign and malign to be able easily assess if there are any differences in the classification of the images of both classes.

The classification results are depicted in Table 2 for the CC view and in Table 3 for the MLO view. As the proposed method is applied in the medical area, standard test parameters such as false positive rate, false negative rate, sensitivity, specificity and accuracy of tests are calculated [35, 77]. All data (except data indicated with *) comes from non-normal distribution, so the basic statistics were done using the median, lower and upper quartile and interquartile range (IQR) [22] for all experiments.

Table 2 Results obtained using the proposed method for image classification for craniocaudal view (CC view)
Full size table
Table 3 Results obtained using the proposed method for image classification for mediolateral view (MLO view)
Full size table

Results obtained by FMIR

For the illustrative example, the query image was randomly chosen, then the list of similar images was created. In the Figs. 2 and 3 the same query image with the six most similar images are depicted (six images with the smallest value of the fuzzy distance) for the FMIR variant using the CC view in comparison to method with NCD (Fig. 4). The resulting images are sorted by the fuzzy distance. All resulting images belong to different patients. According to the results in Table 2 the experiment for the variant of FMIR with the best and with the worst accuracy were chosen.

Fig. 2
figure 2

Example of results using FMIR, where fuzzy distance is defined using Bold (Lukasiewicz, Bounded) product & sum for CC view

Full size image
Fig. 3
figure 3

Example of results using FMIR, where fuzzy distance is defined using Minimum & Maximum for CC view

Full size image
Fig. 4
figure 4

Example of results using NCD for CC view

Full size image

The next part is dedicated to image classification – nature determination. The efficiency of FMIR in six variants was assessed, where fuzzy distance is defined in six ways and for the CC and MLO view separately. For the classification of radiographs with the CC view, the FMIR in the variant with Minimum & Maximum was found as the best one. And the same for the MLO view. The variant of FMIR with fuzzy distance defined with Minimum & Maximum shows the greatest accuracy with good false negativity. In the comparison with NCD, NCD gives better results with little difference between all cuts. But FMIR has a smaller false negativity in the variant with Minimum & Maximum, significantly (P-value=0.00578) for the MLO view in the 10 cut than NCD. Generally, 10 cuts give a better result, because the most similar images, should be on the list at the top.

Due to the usage of TF—IDF, FMIR can determine the areas of interest in the image. The Fig. 5 illustrates the position of the most important blocks, with the highest value of TF-IDF, in a radiograph. The top 20 most important blocks were chosen. In the Fig. 5a a benign image can be seen. The selected blocks occur on the edge of the breast. The situation is different on a cancer radiograph. In the cancer radiographs, Fig. 5b, the most important parts are located inside the breast. The meaning of the colors is as follows: the red colored blocks have the highest TF-IDF values and the blue colored block is to the 20-th highest TF-IDF value. The method with NCD does not provide this feature.

Fig. 5
figure 5

Example of the area of the interest in a benign and cancer radiographs for craniocaudal view

Full size image

Results Obtained by NCD

In this section, results obtained using a simpler method with NCD are presented. The process is similar, but with one difference. Instead of the FS-tree, we measure the similarity between two images using NCD (“Normalized compression distance”) with the utilized Bzip2 compression algorithm. Again, it was chosen randomly the query image and similar images were found. In Fig. 4 can be seen of the six most similar images to the same query image as in the cases with FMIR. The FMIR variant brought better results in both presented variants.

Classification results were presented and compared with the results of FMIR in 9.1.

Conclusion

In the article, the novel method fuzzy medical image retrieval (FMIR) for image retrieval and classification was presented. FMIR is based on vector quantization, fuzzy signatures and fuzzy S-trees. The proposed method was compared in six variants (six variants of fuzzy distance definition) with the method using NCD. It was demonstrated, that FMIR is useful for finding similar images and classification – determination of the nature of query image, if it is malign or benign. In comparison with NCD in classification, it gives us comparable, but a little bit worse results. But FMIR brings significantly smaller false negativity in variant with Minimum & Maximum in fuzzy distance definition, which is very dangerous in breast cancer. Moreover, FMIR has a useful feature, it is able to determine the areas of interest in the picture. FMIR use for finding the area of interest and for the finding of similar images and the method with NCD for classification.

The proposed methods are going to be parts of the complex decision support system to help determine appropriate health care according to the experiences obtained from similar, previous cases. The method was verified on medical data concretely on the breast cancer radiographs (X-ray images). According to the results of the experiments, it was found, that from the clinical point of view, the methods are more useful for finding pathological structures in the part of the body, which are more homogenous in the population such as the liver or other internal organs, where the influence of body shape, or other parts of human body is small. The usage of the proposed method is dependent upon the existence of a large dataset of images, the next work is going to be focused on the enabling and simplification of work with such a huge collection.