Abstract
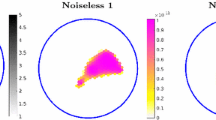
The size estimates approach for Electrical Impedance Tomography (EIT) allows for estimating the size (area or volume) of an unknown inclusion in an electrical conductor by means of one pair of boundary measurements of voltage and current. In this paper we show by numerical simulations how to obtain such bounds for practical application of the method. The computations are carried out both in a 2-D and a 3-D setting.
Similar content being viewed by others
References
Alessandrini, G.: Stable determination of conductivity by boundary measurements. Appl. Anal. 27, 153–172 (1988)
Mandache, N.: Exponential instability in an inverse problem for the Schrödinger equation. Inverse Probl. 17, 1435–1444 (2001)
Alessandrini, G., Vessella, S.: Lipschitz stability for the inverse conductivity problem. Adv. Appl. Math. 35, 207–241 (2005)
Friedman, A.: Detection of mines by electric measurements. SIAM J. Appl. Math. 47, 201–212 (1987)
Friedman, A., Gustafsson, B.: Identification of the conductivity coefficient in an elliptic equation. SIAM J. Math. Anal. 18, 777–787 (1987)
Friedman, A., Isakov, V.: On the uniqueness in the inverse conductivity problem with one measurement. Indiana Univ. Math. J. 38, 563–579 (1989)
Alessandrini, G., Isakov, V.: Analyticity and uniqueness for the inverse conductivity problem. Rend. Ist. Mat. Univ. Trieste 28, 351–370 (1996)
Fabes, E., Kang, H., Seo, J.K.: Inverse conductivity problem with one measurement: error estimates and approximate identification for perturbed disks. SIAM J. Math. Anal. 30, 699–720 (1999)
Alessandrini, G., Isakov, V., Powell, J.: Local uniqueness in the inverse conductivity problem with one measurement. Trans. Am. Math. Soc. 347, 3031–3041 (1995)
Isakov, V.: On uniqueness of recovery of a discontinuous conductivity coefficient. Commun. Pure Appl. Math. 41, 865–877 (1988)
Isakov, V.: Inverse Problems for Partial Differential Equations. Springer, New York (1998)
Di Cristo, M., Rondi, L.: Examples of exponential instability for inverse inclusion and scattering problems. Inverse Probl. 19, 685–701 (2003)
Alessandrini, G., Rosset, E.: The inverse conductivity problem with one measurement: bounds on the size of the unknown object. SIAM J. Appl. Math. 58, 1060–1071 (1998)
Kang, H., Seo, J.K., Sheen, D.: The inverse conductivity problem with one measurement: stability and estimation of size. SIAM J. Math. Anal. 28, 1389–1405 (1997)
Alessandrini, G., Rosset, E., Seo, J.K.: Optimal size estimates for the inverse conductivity problem with one measurement. Proc. Am. Math. Soc. 128, 53–64 (2000)
Alessandrini, G., Morassi, A., Rosset, E.: Size estimates. In: Alessandrini, G., Uhlmann, G. (eds.) Inverse Problems: Theory and Applications. Contemp. Math., vol. 333, pp. 1–33. American Mathematical Society, Providence (2003)
Ikehata, M.: Size estimation of inclusion. J. Inverse Ill-Posed Probl. 6, 127–140 (1998)
Alessandrini, G., Morassi, A., Rosset, E.: Detecting an inclusion in an elastic body by boundary measurements. SIAM Rev. 46, 477–498 (2004). Revised and updated version of SIAM J. Math. Anal. 3, 1247–1268 (2002)
Alessandrini, G., Bilotta, A., Formica, G., Morassi, A., Rosset, E., Turco, E.: Numerical size estimates of inclusions in elastic bodies. Inverse Probl. 21, 133–151 (2005)
Cheng, K.S., Isaacson, D., Newell, J.C., Gisser, D.G.: Electrode models for electric current computed tomography. IEEE Trans. Biomed. Eng. 36, 918–924 (1989)
Paulson, K., Breckon, W., Pidcock, M.: Electrode modelling in electrical impedance tomography. SIAM J. Appl. Math. 52, 1012–1022 (1992)
Somersalo, E., Cheney, M., Isaacson, D.: Existence and uniqueness for the electrode models for electric current computed tomography. SIAM J. Appl. Math. 52, 1023–1040 (1992)
Alessandrini, G., Rosset, E.: Volume bounds of inclusions from physical EIT measurements. Inverse Probl. 20, 575–588 (2004)
Aristodemo, M.: A high-continuity finite element model for two-dimensional elastic problems. Comput. Struct. 21, 987–993 (1985)
Bilotta, A., Formica, G., Turco, E.: Performances of a high-continuity finite element in three-dimensional elasticity. Report LabMeC No. 26, www.labmec.unical.it, 2003; submitted to Computer and Structures
Surowiec, A.J., Stuchly, S.S., Barr, J.R., Swarup, A.: Dielectric properties of breast carcinoma and the surrounding tissues. IEEE Trans. Biomed. Eng. 35, 257–263 (1988)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Alessandrini, G., Bilotta, A., Morassi, A. et al. Computing Volume Bounds of Inclusions by Eit Measurements. J Sci Comput 33, 293–312 (2007). https://doi.org/10.1007/s10915-007-9153-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-007-9153-9