Skip to main content
SpringerLink
Log in

The Shifted Box Scheme for Scalar Transport Problems

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

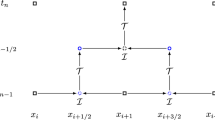
When solving certain scalar transport problems, it is important to use fast methods that do not produce any parasitic oscillating solutions, but still have good energy conservation properties. The well known box scheme has these properties, but the use is restricted by severe conditions on the sign of the coefficients. In order to avoid this restriction, we introduce a modified method, that we call the shifted box scheme. It is very efficient for initial-boundary value problems, since it does not require more work per time step than an explicit scheme, while still being unconditionally stable.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Al-Zanaidi M., Chawla M.A. (2002). A high-accuracy box scheme for first-order systems on hyperbolic conservation laws. Neural Parallel Sc. Comput. 10, 423–430

    MATH  MathSciNet  Google Scholar 

  2. Bradshaw P., Cebeci T., Whitelaw J.H. (1981). Engineering Calculation Methods for Turbulent Flow. Academic Press, New York, NY

    MATH  Google Scholar 

  3. Cebeci K.B., Chang T. (1980). Solution of a hyperbolic system of turbulence-model by the box scheme. Comput. Methods Appl. Mech. Eng. 22, 213–227

    Article  MATH  MathSciNet  ADS  Google Scholar 

  4. Cebeci K.H.B., T.W. PG (1979). Seperating boundary layer flow calculations. J. Comput. Phys. 31, 363–378

    Article  CAS  MATH  MathSciNet  ADS  Google Scholar 

  5. Hong Y., Liu J.L. (2004). Multisimplexity of centered box scheme for a class of Hamiltonian PDEs and an application to quasi-periodically solitary waves. Math. Comput. Modell. 39, 1035–1047

    Article  MATH  MathSciNet  ADS  Google Scholar 

  6. Keller H.B. (1971). A new difference scheme for parabolic problems. In: Hubbard B. (eds). Numerical solution of Partial Differential Equations, vol. 2, Academic, New York, pp. 327–350

    Google Scholar 

  7. Keller H.B. (1978). Numerical methods in boundary-layer theory. Ann. Rev. Fluid Mech. 10, 417–433

    Article  MATH  ADS  Google Scholar 

  8. Lam R.B.S., D.C.L (1976). Central differencing and the box scheme for diffusion convection problems. J. Comput. Phys. 22, 486–500

    Article  MATH  Google Scholar 

  9. Wendroff B. (1960). On centered difference equations for hyperbolic systems. J. Soc. Ind. Appl. Math. 8, 549–555

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Division of Scientific Computing, Uppsala University, Box 337, SE-75105, Uppsala, Sweden

    Bertil Gustafsson

  2. Institute of Computational Mathematics in Engineering (ICME), Stanford University, California, USA

    Bertil Gustafsson

  3. Department of Mechanical Engineering, Stanford University, California, USA

    Yaser Khalighi

Authors
  1. Bertil Gustafsson
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yaser Khalighi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bertil Gustafsson.

Additional information

Dedicated to David Gottlieb on the occasion of his 60th anniversary.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gustafsson, B., Khalighi, Y. The Shifted Box Scheme for Scalar Transport Problems. J Sci Comput 28, 319–335 (2006). https://doi.org/10.1007/s10915-006-9079-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-006-9079-7

Keywords

Search

Navigation