Skip to main content
SpringerLink
Log in

Building Blocks for Arbitrary High Order Discontinuous Galerkin Schemes

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

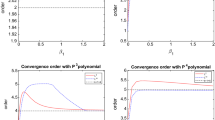
In this article we propose the use of the ADER methodology of solving generalized Riemann problems to obtain a numerical flux, which is high order accurate in time, for being used in the Discontinuous Galerkin framework for hyperbolic conservation laws. This allows direct integration of the semi-discrete scheme in time and can be done for arbitrary order of accuracy in space and time. The resulting fully discrete scheme in time does not need more memory than an explicit first order Euler time-stepping scheme. This becomes possible because of an extensive use of the governing equations inside the numerical scheme itself via the so-called Cauchy–Kovalewski procedure. We give an efficient algorithm for this procedure for the special case of the nonlinear two-dimensional Euler equations. Numerical convergence results for the nonlinear Euler equations results up to 8th order of accuracy in space and time are shown

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Arora M., and Roe P.L. (1997). A well-behaved TVD limiter for high-resolution calculations of unsteady flow. J. Comput. Phys. 132:3–11

    Article  MathSciNet  MATH  ADS  Google Scholar 

  2. Atkins H., and Shu C.W. (1998). Quadrature-free implementation of the discontinuous Galerkin method for hyperbolic equations. AIAA J 36:775–782

    Article  Google Scholar 

  3. Ben-Artzi M., and Falcovitz J. (1984). A second-order Godunov-type scheme for compressible fluid dynamics. J. Comput. Phys 55:1–32

    Article  ADS  MathSciNet  MATH  Google Scholar 

  4. Cockburn, B., Karniadakis, G. E., and Shu, C. W. (2000). Discontinuous Galerkin Methods. Lecture Notes in Computational Science and Engineering, Springer

  5. Cockburn B., and Shu C.W. (1989). TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws II: general framework. Math. Comput 52:411–435

    Article  MathSciNet  MATH  Google Scholar 

  6. Cockburn B., Lin S.Y., and Shu C.W. (1989). TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws III: one dimensional systems. J. Comput. Phys 84:90–113

    Article  MathSciNet  MATH  ADS  Google Scholar 

  7. Cockburn B., Hou S., and Shu C.W. (1990). The Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws IV: the multidimensional case. Math. Comput 54:545–581

    Article  MathSciNet  MATH  Google Scholar 

  8. Cockburn B., and Shu C.W. (1998). The Runge-Kutta discontinuous Galerkin method for conservation laws V: multidimensional systems. J. Comput. Phys 141:199–224

    Article  MathSciNet  MATH  ADS  Google Scholar 

  9. Dumbser M. (2005). Arbitrary High Order Schemes for the Solution of Hyperbolic Conservation Laws in Complex Domains. Shaker Verlag, Aachen

    Google Scholar 

  10. Dumbser M., and Munz C.D. (2005). Arbitrary high order discontinuous Galerkin schemes. Numerical methods for hyperbolic and kinetic problems, In Cordier, S., Goudon, T., Gutnic, M., and Sonnendrucker, E. (eds.), IRMA series in mathematics and theoretical physics, EMS Publishing House, pp. 295–333

  11. Dyson, R. W. (2001). Technique for very high order nonlinear simulation and validation. Technical Report TM-2001-210985, NASA

  12. Hu C., and Shu C.W. (1999). Weighted essentially non-oscillatory schemes on triangular meshes. J. Comput. Phys 150:97–127

    Article  ADS  CAS  MathSciNet  MATH  Google Scholar 

  13. Käser M.A., and Iske A. (2005). ADER schemes on adaptive triangular meshes for scalar conservation laws. J. Comput. Phys 205:486–508

    Article  ADS  MathSciNet  MATH  Google Scholar 

  14. Qiu J., Dumbser M., and Shu C.W. (2005). The discontinuous Galerkin method with Lax-Wendroff type time discretizations. Comput. Method Appl. M 194:4528–4543

    MathSciNet  MATH  Google Scholar 

  15. Qiu J., and Shu C.W. (2003). Hermite WENO schemes and their application as limiters for Runge-Kutta discontinuous Galerkin method: one-dimensional case. J. Comput. Phys 193:115–135

    Article  ADS  CAS  MathSciNet  Google Scholar 

  16. Schwartzkopff T., Dumbser M., and Munz C.D. (2004). Fast high order ADER schemes for linear hyperbolic equations. J. Comput. Phys 197:532–539

    Article  ADS  MATH  Google Scholar 

  17. Schwartzkopff T., Munz C.D., and Toro E.F. (2002). ADER: A high order approach for linear hyperbolic systems in 2D. J. Sci. Comput 17(1-4):231–240

    Article  MathSciNet  MATH  Google Scholar 

  18. Schwartzkopff T., Munz C.D., Toro E.F., and Millington R.C. (2001). The ADER approach in 2D. In: Sonar T (eds). Discrete Modelling and Discrete Algorithms on Continuum Mechanics. Logos Verlag, Berlin, pp. 207–216

    Google Scholar 

  19. Stroud A.H. (1971). Approximate Calculation of Multiple Integrals. Prentice-Hall Inc., Englewood Cliffs, New Jersey

    MATH  Google Scholar 

  20. Titarev V.A., and Toro E.F. (2002). ADER: Arbitrary high order Godunov approach. J. Sci. Comput 17(1-4):609–618

    Article  MathSciNet  MATH  Google Scholar 

  21. Titarev V.A., and Toro E.F. (2005). ADER schemes for three-dimensional nonlinear hyperbolic systems. J. Comput. Phys 204:715–736

    Article  ADS  MathSciNet  MATH  Google Scholar 

  22. Toro E.F. (1999). Riemann Solvers and Numerical Methods for Fluid Dynamics. Springer, second edition

  23. Toro, E. F., Millington, R. C., and Nejad, L. A. M. (2001). Towards very high order Godunov schemes. In Toro, E. F. (ed.), Godunov Methods. Theory and Applications, Kluwer/Plenum Academic Publishers. pp. 905–938

  24. Toro, E. F., and Titarev, V. A. (2002). Solution of the generalized Riemann problem for advection-reaction equations. Proc. Roy. Soc. London, pages 271–281

Download references

Author information

Authors and Affiliations

  1. Institut für Aerodynamik und Gasdynamik, University of Stuttgart, Pfaffenwaldring 21, D-70550, Stuttgart, Germany

    Michael Dumbser & Claus-Dieter Munz

Authors
  1. Michael Dumbser
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Claus-Dieter Munz
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Michael Dumbser.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dumbser, M., Munz, CD. Building Blocks for Arbitrary High Order Discontinuous Galerkin Schemes. J Sci Comput 27, 215–230 (2006). https://doi.org/10.1007/s10915-005-9025-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-005-9025-0

Keywords

Search

Navigation