Skip to main content
SpringerLink
Log in

Analytic approximation to delayed convection dominated systems through transforms

  • Original Paper
  • Published:
Journal of Mathematical Chemistry Aims and scope Submit manuscript

Abstract

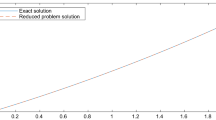
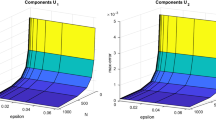
In this paper we consider a family of singularly perturbed delay differential equation of convection diffusion type. When the perturbation parameter is very small, the solution of the problem exhibits layer behavior. In the layer region the solution changes rapidly, while away from this region the change in the solution is moderate. This simultaneous presence of two different scales phenomena makes the problem stiff. In this work, the problem is solved by applying a new Liouville–Green transform and the asymptotic solutions are obtained. Application to multi-point boundary value problem is also illustrated. Several test examples are taken into account so as to test the efficiency of the proposed method. The method presented is compared with other existing numerical or asymptotic methods. It is observed that the method presented is very easy to implement and is capable of reducing the size of calculations significantly while still maintaining high accuracy of the solution.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. H.G. Roos, M. Stynes, L. Tobiska, Numerical Methods for Singularly Perturbed Differential Equations (Springer, Berlin, 1996)

    Book  Google Scholar 

  2. J.J.H. Miller, E. ORiordan, G.I. Shishkin, Fitted Numerical Methods for Singular Perturbation Problems, Error Estimates in the Maximum Norm for Linear Problems in One and Two Dimensions (World Scientific, Singapore, 1996)

    Book  Google Scholar 

  3. R.E. O’Malley, Singular Perturbation Methods for Ordinary Differential Equations, Applied Mathematical Sciences 89 (Springer, Berlin, 1990)

    Google Scholar 

  4. J.K. Knowles, R.E. Messick, On a class of singular perturbation problems. J. Math. Anal. Appl. 9, 42–58 (1964)

    Article  Google Scholar 

  5. R.R. Gold, Magnetohydrodynamic pipe flow. Part I. J. Fluid Mech. 13, 505–512 (1962)

    Article  Google Scholar 

  6. A. Kaushik, Singular perturbation analysis of bistable differential equation arising in the nerve pulse propagation. Nonlinear Anal. 09, 2106–2127 (2008)

    Article  Google Scholar 

  7. A. Kaushik, M.D. Sharma, Numerical analysis of a mathematical model for propagation of an electrical pulse in a neuron. Numer. Methods Partial Differ. Equ. 27, 1–18 (2008)

    Google Scholar 

  8. M.K. Kadalbajoo, K.K. Sharma, Numerical treatment of a mathematical model arising from a model of neuronal variability. J. Math. Anal. Appl. 307, 606–627 (2005)

    Article  Google Scholar 

  9. A. Kaushik, Nonstandard perturbation approximation and traveling wave solutions of non-linear reaction diffusion equations. Numer. Methods Partial Differ. Equ. 24, 217–238 (2008)

    Article  Google Scholar 

  10. R.E. O’Malley, Introduction to Singular Perturbations (Academic Press, New York, 1974)

    Google Scholar 

  11. J.J.H. Miller, Singular Perturbation Problems in Chemical Physics, Analytic and Computational Methods XCVII (Wiley, New York, 1997)

    Google Scholar 

  12. T. Lin\(\beta \), An upwind difference scheme on a novel Shishkin type mesh for a linear convection diffusion problem. J. Comput. Appl. Math. 110, 93–104 (1999)

  13. M.K. Kadalbajoo, K.K. Sharma, Numerical analysis of singularly perturbed delay differential equations with layer behavior. Appl. Math. Comput. 157, 11–28 (2004)

    Article  Google Scholar 

  14. M.K. Kadalbajoo, K.K. Sharma, Numerical analysis of boundary-value problems for singularly perturbed differential-difference equations: small shifts of mixed type with rapid oscillations. Commun. Numer. Methods in Eng. 20, 167–182 (2004)

    Article  Google Scholar 

  15. A. Kaushik, M. Sharma, Convergence analysis of weighted difference approximations on piecewise uniform grids to a singularly perturbed functional differential equations. J. Optim. Theory Appl. 155, 252–272 (2012)

    Article  Google Scholar 

  16. A. Kaushik, M. Sharma, A Robust numerical approach for singularly perturbed time delayed parabolic partial differential equations. Comput. Math. Model. 23, 96–106 (2012)

    Article  Google Scholar 

  17. V. John, J. Maubach, L. Tobiska, Nonconforming streamline diffusion finite element methods for convection diffusion problems. Numer. Math. 78, 165–188 (1997)

    Article  Google Scholar 

  18. F. Schieweck, L. Tobiska, A nonconforming finite element method of upstream type applied to the stationary Navier–Stokes equation. RAIRO Modél. Math. Anal. Numér. 23, 627–647 (1989)

    Google Scholar 

  19. D. Kay, D. Silvester, The reliability of local error estimators for convection diffusion equations. IMA J. Numer. Anal. 21, 107–122 (2001)

    Article  Google Scholar 

  20. A. Kaushik, V. Kumar, M. Sharma, Analysis of factorization method for elliptic differential equation. Comput. Math. Model. 22, 98–110 (2011)

    Article  Google Scholar 

  21. A. Kaushik, V. Kumar, A.K. Vashishth, An efficient mixed asymptotic-numerical scheme for singularly perturbed convection diffusion problems. Appl. Math. Comput. 118, 8645–8658 (2012)

    Article  Google Scholar 

  22. A. Kaushik, Iterative analytic approximation to nonlinear convection dominated systems. Comput. Phys. Commun. 184, 2061–2069 (2013)

    Article  CAS  Google Scholar 

  23. T. Lin\(\beta \), M. Stynes, A hybrid difference scheme on a Shishkin mesh for linear convection diffusion problems, APNUM. 31, 255–270 (1999)

  24. A. Kaushik, K.K. Sharma, M. Sharma, A parameter uniform difference scheme for parabolic partial differential equation with a retarded argument. Appl. Math. Model. 34, 4232–4242 (2010)

    Article  Google Scholar 

  25. J. Kevorkian, J.D. Cole, Perturbation Methods in Applied Mathematics (Springer, New York, 1981)

    Book  Google Scholar 

  26. A.H. Nayfeh, Perturbation Methods (Wiley, New York, 1979)

    Google Scholar 

  27. A. Andargie, Y.N. Reddy, Fitted fourth-order tridiagonal finite difference method for singular perturbation problems. Appl. Math. Comput. 192, 90–100 (2007)

    Article  Google Scholar 

  28. M.M. Chawla, A fourth-order tridiagonal finite difference method for general non-linear two-point boundary value problems with mixed boundary conditions. J. Inst. Maths Appl. 21, 83–93 (1978)

    Article  Google Scholar 

  29. M.M. Chawla, An efficient finite difference method for two-point boundary value problems. Neural Parallel Sci. Comput. 4, 384–396 (1996)

    Google Scholar 

  30. A. Andargie, Y.N. Reddy, An exponentially fitted special second-order finite difference method for solving singular perturbation problems. Appl. Math. Comput. 190, 1767–1782 (2007)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University Institute of Engineering and Technology, Panjab University, Chandigarh, 160014, UT, India

    Aditya Kaushik

  2. Department of Mathematics, KVA DAV College, Karnal, 132001, Haryana, India

    Manju Sharma

  3. Department of Mathematics, Honghe University, Mengzi, 661100, Yunnan, People’s Republic of China

    Chenglin Li

Authors
  1. Manju Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Aditya Kaushik
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chenglin Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Aditya Kaushik.

Additional information

The author greatfully acknowledges financial support from University Grants Commission (New Delhi, India) under Start-up Grant F.20-30(12)/2012(BSR).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sharma, M., Kaushik, A. & Li, C. Analytic approximation to delayed convection dominated systems through transforms. J Math Chem 52, 2459–2474 (2014). https://doi.org/10.1007/s10910-014-0394-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10910-014-0394-1

Keywords

Search

Navigation