Abstract
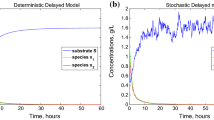
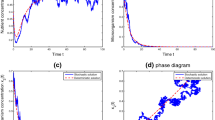
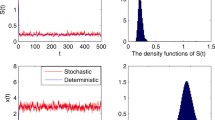
In this paper, we introduce an improved Chemostat model with Crowley–Martin type functional response and time delays. By constructing Lyapunov functionals, the global asymptotic stability of the equilibria is shown in the case of a single species. The conditions for the global asymptotical stability of the model with time delays are obtained via monotone dynamical systems in the case of two species. Our results demonstrate that the effects of predator interference may result in coexistence of two species.
Similar content being viewed by others
References
L. Chen, J. Chen, Nonlinear Biology Dynamics (Science Press, Beijing, 1993)
H.L. Smith, P. Waltman, The Theory of the Chemostat: Dynamics of Microbial Competition (Cambridge University Press, Cambridge, UK, 1995)
L. Wang, G.S.K. Wolkowicz, A delayed chemostat model with general non-monotone response functions and differential removal rates. J. Math. Anal. Appl. 321, 452 (2006)
G.S.K. Wolkowicz, Z. Lu, Global dynamics of a mathematical model of competition in the chemostat: general response functions and differential death rates. SIAM J. Appl. Math. 52, 222 (1992)
G.S.K. Wolkowicz, H. Xia, Global asymptotic behavior of a chemostat model with discrete delays. SIAM J. Appl. Math. 57, 1019 (1997)
S.F. Ellermeyer, Competition in the chemostat: global asymptotic behavior of a model with delayed response in growth. SIAM J. Appl. Math. 54, 456 (1994)
M. White, X. Zhao, A periodic Droop model for two species competition in a chemostat. Bull. Math. Biol. 71, 145 (2009)
Z. Yuan, Z. Qiu, The asymptotic behavior of chemostat model with the Beddington–DeAngelies functional responses. J. Southwest China Normal Uinv. 28, 193 (2009)
Z. Qiu, J. Yu, Y. Zou, The asymptotic behavior of a chemostat model with the Beddington–DeAngelis functional response. Math. Biosci. 187, 175 (2004)
G. Pang, L. Chen, Analysis of a Beddington–DeAngelis food chain chemostat with periodically varying substrate. J. Math. Chem. 44, 467 (2008)
G.T. Skalski, J.F. Gilliam, Functional response with redator interference: viable alternatives to the Holling type II model. Ecology 82, 3083 (2001)
P.H. Crowley, E.K. Martin, Functional responses and interference within and between year classes of a dragonfly population. J. North Am. Benthol. Soc. 8, 211 (1989)
R.K. Upadhyay, R.K. Naji, Dynamics of a three species food chain model with Crowley–Martin type functional response. Chaos Solitons Fractals 42, 1337 (2009)
X. Shi, X. Zhou, X. Song, Analysis of a stage-structured predator–prey model with Crowley–Martin function. J. Appl. Math. Comput. 36, 459 (2011)
S. Sun, R. Zhang, L. Zeng, Qualitative analysis on a chemostat model with the Crowley–Martain functional response. J. Biomath 26, 293 (2011)
Y. Kuang, Delay Differential Equations with Applications in Population Dynamics (Academic Press, San Diego, 1993)
S. Ruan, The dynamics of Chemostat models. J. Cent. China Normal Univ. (Nat. Sci.) 31, 377 (1997)
G. Fu, W. Ma, Chemostat dynamics models described by differential equations (I, II). Microbiology, 31(5), 136 (2004), 31(6), 128 (2004)
G. Huang, Y. Takeuchi, Global analysis on delay epidemiological dynamic models with nonlinear incidence. J. Math. Biol. 63, 125 (2011)
X. Zhang, R. Xu, L. XUE, Global stability for ratio-dependent chemostat model with time delay. J. Ordnance Eng. Coll. 21, 75 (2009)
W. Wang, L. Chen, A predator Cprey system with stage-structure for predator. Comput. Math. Appl. 33, 83 (1997)
Author information
Authors and Affiliations
Corresponding author
Additional information
The research is partially supported by NSFC(11071013), the Funds of the construction of high-level university in Shaanxi province (2012SXTS06) and the Funds of Yanan University (YD2012-03)
Rights and permissions
About this article
Cite this article
Dong, Q., Ma, W. & Sun, M. The asymptotic behavior of a Chemostat model with Crowley–Martin type functional response and time delays. J Math Chem 51, 1231–1248 (2013). https://doi.org/10.1007/s10910-012-0138-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10910-012-0138-z