Skip to main content
SpringerLink
Log in

Double hexagonal chains with minimal total π-electron energy

  • Published:
Journal of Mathematical Chemistry Aims and scope Submit manuscript

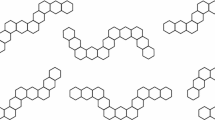
The total energy of all π-electrons in a conjugated hydrocarbon (within the framework of HMO approximation) is the sum of the absolute value of all the eigenvalues of its corresponding graph. In this paper, we consider “double hexagonal chains” as benzenoids constructed by successive fusions of successive naphthalenes along a zig–zag sequence of triples of edges as appear on opposite sides of each naphthalene unit. It is shown that if the fusions are such as to give a polyaceacene then the total π-electron energy is the minimum from among all the double hexagonal chains with the same number of naphthalene units.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Gutman I., Polansky O.E. (1986). Mathematical concepts in organic chemistry. Springer, Berlin

    Google Scholar 

  2. Gutman I., Cyvin S.J. (eds) (1990). Advances in the Theory of benzenoid hydrocarbons. Topi. Curr. Chem., Vol. 153. Springer, Berlin

  3. Gutman I. (eds) (1992). Advances in the Theory of benzenoid hydrocarbons I. Top. Curr. Chem., Vol. 162. Springer, Berlin

  4. Gutman I. (1977). Theoret. Chim. Acta (Berlin) 45: 79

    Article  CAS  Google Scholar 

  5. Gutman I., Hou Y. (2001). MATCH – Commun. Math. Comput. Chem. 43: 17

    CAS  Google Scholar 

  6. Hou Y. (2001). J. Math. Chem. 29: 163

    Article  CAS  Google Scholar 

  7. Hou Y. (2002). Lin. Multilin. Algebra 49: 347

    Article  Google Scholar 

  8. Li H. (1999). J. Math. Chem. 25: 145

    Article  Google Scholar 

  9. Zhang F., Li H. (1999). Discrete Appl. Math. 92: 71

    Article  Google Scholar 

  10. Zhang F., Li Z., Wang L. (2001). Chem. Phys. Lett. 337: 125

    Article  CAS  Google Scholar 

  11. Zhang F., Li Z., Wang L. (2001). Chem. Phys. Lett. 337: 131

    Article  CAS  Google Scholar 

  12. Seitz W.A., Klein D.J. (eds) (1985). Chem. Phys. Lett. 115: 139.

  13. Klein D.J., Schmalz T.G. (eds) (1985). Chem. Phys. Lett. 120: 367.

  14. Cvetkovic D.M., Doob M., Gutman et al. I. (1988). Ann. Discrete Math. 36: 50

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Qinghai Normal University, Xining, Qinghai, 810008, P.R. China

    Haizhen Ren

  2. School of Mathematical Sciences, Xiamen University, Xiamen, Fujian, 361005, P.R. China

    Fuji Zhang

Authors
  1. Haizhen Ren
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fuji Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Haizhen Ren.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ren, H., Zhang, F. Double hexagonal chains with minimal total π-electron energy. J Math Chem 42, 1041–1056 (2007). https://doi.org/10.1007/s10910-006-9159-9

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10910-006-9159-9

Keywords

AMS subject classification

Search

Navigation