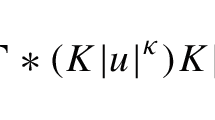Abstract
We revisit the problem of the calculation of zero-temperature properties for the dilute two-dimensional Bose gas. By using Popov’s hydrodynamic approach and perturbation theory on the two-loop level, we recover not only the known expansion for the ground-state energy but also calculate for the first time the condensate density and Tan’s contact.

Similar content being viewed by others
References
A. Posazhennikova, Phys. Rev. Mod. 78, 1111 (2006)
Z. Hadzibabic, J. Dalibard, Riv. Nuovo Cim. 34, 389 (2011)
Z. Hadzibabic, P. Kruger, M. Cheneau, B. Battelier, J. Dalibard, Nature 441, 1118 (2006)
P. Cladé, C. Ryu, A. Ramanathan, K. Helmerson, W.D. Phillips, Phys. Rev. Lett. 102, 170401 (2009)
T. Yefsah, R. Desbuquois, L. Chomaz, K.J. Günter, J. Dalibard, Phys. Rev. Lett. 107, 130401 (2011)
R. Desbuquois, L. Chomaz, T. Yefsah, J. Leonard, J. Beugnon, C. Weitenberg, J. Dalibard, Nat. Phys. 8, 645 (2012)
M.S. Mashayekhi, J.-S. Bernier, D. Borzov, J.-L. Song, F. Zhou, Phys. Rev. Lett. 110, 145301 (2013)
L. Salasnich, Phys. Rev. Lett. 118, 130402 (2017)
S.R. Beane, Eur. Phys. J. D 72, 55 (2018)
M. Schick, Phys. Rev. A 3, 1067 (1971)
V.N. Popov, Theor. Math. Phys. 11, 565 (1972)
Yu.E. Lozovik, V.I. Yudson, Physica A 93, 493 (1978)
E.B. Kolomeisky, J.P. Straley, Phys. Rev. B 46, 11749 (1992)
A.A. Ovchinnikov, J. Phys. Condens. Matter. 5, 8665 (1993)
A.Yu. Cherny, A.A. Shanenko, Phys. Rev. E 64, 027105 (2001)
J.O. Andersen, Eur. Phys. J. B 28, 389 (2002)
C. Mora, Y. Castin, Phys. Rev. A 67, 053615 (2003)
C. Mora, Y. Castin, Phys. Rev. Lett. 102, 180404 (2009)
G.E. Astrakharchik, J. Boronat, I.L. Kurbakov, Yu.E. Lozovik, F. Mazzanti, Phys. Rev. A 81, 013612 (2010)
S.R. Beane, Phys. Rev. A 82, 063610 (2010)
L. Pricoupenko, Phys. Rev. A 84, 053602 (2011)
B. Abdelâali, Phys. Rev. A 86, 043608 (2012)
G.E. Astrakharchik, J. Boronat, J. Casulleras, I.L. Kurbakov, Yu.E. Lozovik, Phys. Rev. A 79, 051602(R) (2009)
L.-C. Ha, C.-L. Hung, X. Zhang, U. Eismann, S.-K. Tung, C. Chin, Phys. Rev. Lett. 110, 145302 (2013)
F. Mazzanti, A. Polls, A. Fabrocini, Phys. Rev. A 71, 033615 (2005)
S. Pilati, J. Boronat, J. Casulleras, S. Giorgini, Phys. Rev. A 71, 023605 (2005)
C.C. Chien, J.H. She, F. Cooper, Ann. Phys. 347, 192 (2014)
A.G. Volosniev, H.-W. Hammer, N.T. Zinner, Phys. Rev. A 92, 023623 (2015)
P. Konietin, V. Pastukhov, J. Low Temp. Phys. 190, 256 (2018)
V.N. Popov, Functional Integrals and Collective Excitations (Cambridge University Press, Cambridge, 1987)
E. Braaten, A. Nieto, Eur. Phys. J. B 11, 143 (1999)
V. Pastukhov, J. Low Temp. Phys. 186, 148 (2017)
R. Combescot, F. Alzetto, X. Leyronas, Phys. Rev. A 79, 053640 (2009)
M. Valiente, N.T. Zinner, K. Mølmer, Phys. Rev. A 84, 063626 (2011)
S. Tan, Ann. Phys. 323, 2952 (2008)
E. Braaten, L. Platter, Phys. Rev. Lett. 100, 205301 (2008)
V. Pastukhov, Ann. Phys. 372, 149 (2016)
V. Pastukhov, Phys. Rev. A 95, 023614 (2017)
N.M. Hugenholtz, D. Pines, Phys. Rev. 116, 489 (1959)
A.M.J. Schakel, arXiv:1007.3452
F. Werner, Y. Castin, Phys. Rev. A 86, 053633 (2012)
Acknowledgements
We thank Prof. A. Rovenchak for stimulating discussions. This work was partly supported by Project FF-30F (No. 0116U001539) from the Ministry of Education and Science of Ukraine.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendices
1.1 A
The explicit analytic expressions for the diagrams determining corrections to the partition function logarithm \(-\beta \Delta E\) and presented in Fig. (1) are the following
(recall that \(|\mathbf{k}|,|\mathbf{q}|, |\mathbf{s}|<\varLambda \) and \(\alpha _k=E_k/\varepsilon _k\)), where the frequency sums in the diagrams b and c
and in e and d
were evaluated with the help of residue theorem in the zero-temperature limit.
1.2 B
In this section, we present some details of calculation of integrals determining constants in the ground-state energy (17), condensate depletion (18) and contact (20). We will not stop on the evaluation of variational derivatives \(\left( \frac{\delta E}{\delta \varepsilon _k}\right) _{n,\mathcal {T}}\), \(\left( \frac{\delta E}{\delta \mathcal {T}_k}\right) _{n}\) with the following integration in \(\mathbf{k}\)-space and only give the dimensionless expressions written in terms of triple integrals. After elimination of the explicit dependence on cutoff parameter \(\varLambda \) for \(\text {const}_E\), we obtained
here and below
The second-order correction to condensate density is determined by the following constant
Finally, \(\text {const}_{\mathcal {C}}\) after some rearrangements is given by
The results of numerical calculations of these integrals are presented in main text.
Rights and permissions
About this article
Cite this article
Pastukhov, V. Ground-State Properties of a Dilute Two-Dimensional Bose Gas. J Low Temp Phys 194, 197–208 (2019). https://doi.org/10.1007/s10909-018-2082-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10909-018-2082-1