Kinematics of the Doped Quantum Vortices in Superfluid Helium Droplets

Abstract

Recent observation of quantum vortices in superfluid $^{4}$He droplets measuring a few hundreds of nanometers in diameter involved decoration of vortex cores by clusters containing large numbers of Xe atoms, which served as X-ray contrast agents. Here, we report on the study of the kinematics of the combined vortex–cluster system in a cylinder and in a sphere. Equilibrium states, characterized by total angular momentum, L, were found by minimizing the total energy, E, which sums from the kinetic energy of the liquid due to the vortex and due to orbiting Xe clusters, as well as solvation energy of the cluster in the droplet. Calculations show that, at small mass of the cluster, the equilibrium displacement of the system from the rotation axis is close to that for the bare vortex. However, upon decrease in L beyond certain critical value, which is larger for heavier clusters, the displacement bifurcates toward the surface region, where the motion of the system is governed by the clusters. In addition, at even smaller L, bare orbiting clusters become energetically favorable, opening the possibility for the vortex to detach from the cluster and to annihilate at the droplet’s surface.

Appendix

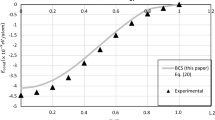
In order to calculate $E_{\mathrm{vort}}$, $L_{\mathrm{vort}}$, and $\omega = {\mathrm{d}E}/{\mathrm{d}L}$, of a bare curved vortex with different core size in spherical He droplets, Eqs. (3) and (4) are used. Numeric calculations of the angular momentum via Eq. (3) is straightforward. On the other hand, the energy calculation takes a much longer time. To expedite the calculations, a summation method can be utilized by dividing a certain two-dimensional area of the integration, close to the vortex into smaller discrete areas. However, even then the values of energy show some noise, since the smaller discrete areas of integration are still much larger than the required infinitesimal areas of integration. On the other hand, we found that, the results of the LIA calculations of the $E_{\mathrm{vort}}$ and $L_{\mathrm{vort}}$ versus r / R for a bare vortex could be well-fitted by a function

$$\begin{aligned} f \left( \frac{r}{R}\right) =1-a+a\cdot \cos \left( {\frac{\pi \cdot \frac{r}{R}}{b}} \right) . \end{aligned}$$

(A.1)

The parameters a and b have been obtained from a limited number of high accuracy calculations of $E_{\mathrm{vort}}$ and $L_{\mathrm{vort}}$ at different displacement for 0.1, 2.5, 5 and 10 nm. Table 1 gives the obtained parameters. The resulting fitted dependencies are presented in Fig. 5 and were used to obtain the continuous outcome curves presented in Fig. 3. In Fig. 5, the $E_{\mathrm{vort}}$ and $L_{\mathrm{vort}}$ are expressed in units of the corresponding values for central rectilinear vortex with the core radius of $\xi$, which are given by Eqs. (11, 12). It is seen that the reduced values of energy, angular momentum and angular velocity for bare vortices with different core sizes are very similar.

Table 1 Parameters a and b in Eq. (A.1) used to fit $E_{\mathrm{vort}}$ and $L_{\mathrm{vort}}$ versus r / R

Fig. 5

Reduced energy, reduced angular momentum in panel (a) and angular velocity in panel (b) of a bare vortex with core radius of $\xi = 0.1, 2.5, 5$ and 10 nm versus the reduced displacement from the droplet’s center in the droplet having $R= 100\,\hbox {nm}$ (Color figure online)