Skip to main content
SpringerLink
Log in

Quantum Turbulence in Coflow of Superfluid \(^{4}\)He

  • Published:
Journal of Low Temperature Physics Aims and scope Submit manuscript

Abstract

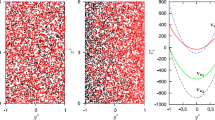
We study numerically nonuniform quantum turbulence of coflow in a square channel by the vortex filament model. Coflow means that superfluid velocity \(\varvec{v}_\mathrm{s}\) and normal fluid velocity \(\varvec{v}_\mathrm{n}\) flow in the same direction. Quantum turbulence for thermal counterflow has been long studied theoretically and experimentally. In recent years, experiments of coflow have been performed to observe different features from thermal counterflow. By supposing that \(\varvec{v}_\mathrm{s}\) is uniform and \(\varvec{v}_\mathrm{n}\) takes the Hagen–Poiseuille profile, simulations find that quantized vortices are distributed inhomogeneously. Vortices like to accumulate on the surface of a cylinder with \(\varvec{v}_\mathrm{s} \simeq \varvec{v}_\mathrm{n}\). Consequently, the vortex configuration becomes degenerate from three-dimensional to two-dimensional.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. E. Varga, S. Babuin, L. Skrbek, Phys. Fluids 27, 065101 (2015)

    Article  ADS  Google Scholar 

  2. R.J. Donnelly, Quantized Vortices in Helium II (Cambridge University Press, Cambridge, 1995), pp. 42–45

    Google Scholar 

  3. R.P. Feynman, Progress in Low Temperature Physics, vol. 1 (Elsevier, Amsterdam, 1955)

    Google Scholar 

  4. K.W. Schwarz, Phys. Rev. B 38, 2398 (1988)

    Article  ADS  Google Scholar 

  5. H. Adachi, S. Fujiyama, M. Tsubota, Phys. Rev. B 81, 104511 (2010)

    Article  ADS  Google Scholar 

  6. K.W. Schwarz, Phys. Rev. B 31, 5782 (1985)

    Article  ADS  Google Scholar 

  7. R.W. Johnson, The Handbook of Fluid Dynamics (CRC, Boca Raton, 1998)

    MATH  Google Scholar 

  8. S. Yui, M. Tsubota, Phys. Rev. B 91, 184504 (2015)

    Article  ADS  Google Scholar 

Download references

Acknowledgments

M. T. was supported by JSPS KAKENHI Grant No. 26400366 and MEXT KAKENHI ”Fluctuation & Structure” Grant No. 26103526.

Author information

Authors and Affiliations

  1. Department of Physics, Osaka City University, Sugimoto 3-3-138, Sumiyoshi-ku, Osaka, 558-8585, Japan

    S. Ikawa & M. Tsubota

  2. The OCU Advanced Research Institute for Natural Science and Technology (OCARINA), Osaka, Japan

    M. Tsubota

Authors
  1. S. Ikawa
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Tsubota
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Ikawa.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ikawa, S., Tsubota, M. Quantum Turbulence in Coflow of Superfluid \(^{4}\)He. J Low Temp Phys 183, 230–237 (2016). https://doi.org/10.1007/s10909-016-1578-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10909-016-1578-9

Keywords

Search

Navigation