Flux Dynamics, ac Losses, and Activation Energies in (Ba$_{0.6}$K$_{0.4})$Fe$_{2}$As$_{2}$ Bulk Superconductor

Abstract

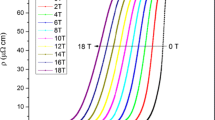
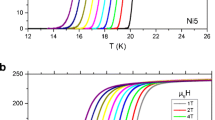
Flux pinning and thermally assisted flux flow are studied in a (Ba$_{0.6}$K$_{0.4})$Fe$_{2}$As$_{2}(T_\mathrm{c}$=38.3 K) bulk samples in magnetic fields up to 18 T via ac susceptibility measurements. Ac susceptibility curves shift to higher temperatures as the frequency is increased from 75 to 1,997 Hz in all fields. The frequency ($f)$ shift of the susceptibility curves is modeled by the Anderson-Kim Arrhenius law $f = f_{0}\mathrm{exp}(-E_\mathrm{a}{ /kT})$ to determine flux activation energy $E_\mathrm{a}/k$ as a function of ac field $H_\mathrm{ac}$ and dc magnetic flux density $\mu$ $_\mathrm{0} H_\mathrm{dc}$. $E_\mathrm{a}/k$ ranges from 8,822 K (761 meV) at $\mu$ $_{0} H_{dc}$ = 0 T to 1,100 K (95 meV) at 18 T for $H_\mathrm{ac}=$80 A/m (1 Oe). The energies drop very quickly in a non-linear manner as $\mu$ $_{0} H_\mathrm{dc}$ increases from 0 to 1 T, and more gradually, in a linear-like manner, as $\mu$ $_{0} H_\mathrm{dc}$ increases further to 18 T, suggesting some kind of vortex transition. For ac fields of 400 A/m (5 Oe) and higher, the Arrhenius model starts breaking down, at around $\mu$ $_{0} H_{ \mathrm dc}$ = 2 T. As the dc magnetic flux density increases further, this breakdown becomes significant for $\mu _{0} H_\mathrm{dc}$ = 15 and 18 T at ac fields of 400 A/m and higher. Extensive mapping of the de-pinning, or irreversibility, lines shows broad dependence on the magnitude of the ac field, frequency, in addition to the dc magnetic flux density.