Skip to main content
SpringerLink
Log in

Vortex Interaction with Mesoscopic Surface Cavities in Superconductors

  • Published:
Journal of Low Temperature Physics Aims and scope Submit manuscript

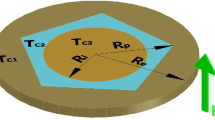
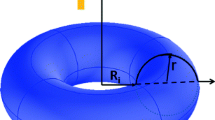
The conformal mapping method is used to study the problem of flux line interaction with surface cavities having cylindrical profile and characteristic size \({\ell < < \lambda}\) , i.e., within mesoscopic scale, where λ is the penetration length. It is shown that the metastable states are achieved when the dimensions of the surface irregularities do not exceed the coherence length ξ. Our study shows that the surface barrier may vanish at some weak point at which the surface irregularities have mesoscopic scales. On the other hand, a remarkable decrease in the surface barrier occurs when the surface defects size \({\ell > > \lambda}\) . Our results are compared with the available experimental data and theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Chen D.X., Hermando A., Conde F., Ramfrez J., Gonzalez-Calbet J.M., Vallet M. (1994). J. Appl. Phys. 75: 2578

    Article  ADS  Google Scholar 

  2. Konczykowski M., Burlachkov L.I., Holtzberg F. (1991). Phys. Rev. B 43: 13703

    Article  ADS  Google Scholar 

  3. Konczykowski M., Burlachkov L.I., Yeshurum Y., Holtzberg F. (1992). Physica C 194: 155

    Article  ADS  Google Scholar 

  4. Kopylov V.N., Koshelev A.E., Schegolev I.F. (1990). Phys. C 170: 291

    Article  ADS  Google Scholar 

  5. Baelus B.J., Peeters F.M. (2002). Phys. Rev. B 65: 104515

    Article  ADS  Google Scholar 

  6. Baelus B.J., Kadowaki K., Peeters F.M. (2005). Phys. Rev. B 71: 024514

    Article  ADS  Google Scholar 

  7. Singha Deo P., Schweigert V.A., Peeters F.M.(1999). Phys. Rev. B 59: 6039

    Article  ADS  Google Scholar 

  8. Ulmaier H.A., Gauster W.F.(1966). J. Appl. Phys. 37: 4519

    Article  ADS  Google Scholar 

  9. Ulmaier H.A.(1966). Phys. Stat. Sol. (b) 17: 631

    Google Scholar 

  10. Campbell A.M., Evetts I.E., Dew-Hughas D. (1968). Philos. Mag. 18: 313

    Google Scholar 

  11. Morozov N., Zedov E., Konczykowski M., Doyle R.A. (1997). Phys. C 291: 113

    Article  ADS  Google Scholar 

  12. Bean C.P., Livingston J.D. (1964). Phys. Rev. Lett. 12: 14

    Article  ADS  Google Scholar 

  13. G. de Gennes Superconductivity of Metals and Alloys, Benjamin, New York (1966), Chapt. 3.

  14. Ternovskii F.F., Shehata L.N.(1972). Sov. Phys. JETP 35: 1202

    Google Scholar 

  15. J. R. Clem, In Low Temp. Phys.-LT-13, K. D. Timmerhaus, W. J. O’Sullivan, and E. F. Hammel, eds., (Plenum Pub. Corp., New York, (1974) Vol. 3 p. 102.

  16. Shehata L.N.(1980). Phys. Stat. Sol. (b) 97: 641

    Google Scholar 

  17. Vodolazov D.Yu.(2000). Phys. Rev. B 62: 8691

    Article  ADS  Google Scholar 

  18. Vodolazov P.Y., Maksimov I.L., Brandt E.H.(2003). Phys. C 384: 211

    Article  ADS  Google Scholar 

  19. P. Galiako, Ekspt. Teoret. Fiz. 50, 717 (1966) [Sov. Phys. JETP 23, 475 (1966)].

  20. Gurevich A.V., Kovachev V.T.(1988). Phys. Stat. Sol. (b) 145: K47

    Google Scholar 

  21. Chikumoto N., Konczykowski M., Motohira N., Kishio K., Kitazawa K. (1991). Phys. C 185–189: 1835

    Article  Google Scholar 

  22. Bussiere J.F.(1976). Phys. Lett. A. 58: 343

    Article  ADS  Google Scholar 

  23. Bussiere J.F., Suenaga M. (1976). J. Appl. Phys. 47: 707

    Article  ADS  Google Scholar 

  24. Bussiere J.F., Kavachev V.T. (1978). J. Appl. Phys. 49: 2526

    Article  ADS  Google Scholar 

  25. Bass F., Freilikher V.D., Shapiro B.Ya., Shvartser M.(1996). Phys. C 260: 231

    Article  ADS  Google Scholar 

  26. Geim A.K., Dubonos S.V., Grigorieva I.V., Novoselov K.S., Peeters F.M., Schweigert V.A.(2000). Nature 407: 55

    Article  ADS  Google Scholar 

  27. Peeters F.M., Schweigert V.A., Baelus B.J.(2002). Phys. C 369: 158

    Article  ADS  Google Scholar 

  28. A. A. Abrikosov, J. Ekspt. Teoret. Fiz. 32, 1442 (1957) [Sov. Phys. JETP 5, 1174 (1957)]; and 46, 1464 (1964) [Sov. Phys. JETP 19, 988 (1964)].

  29. G. S. Mkrchyan and V. V. Schmidt, J. Ekspt. Teoret. Fiz. 61, 367 (1971) [Sov. Phys. JETP 34, 195 (1972)].

    Google Scholar 

  30. Nordborg H., Vinokur V.M. (2000). Phys. Rev. B 62: 12408

    Article  ADS  Google Scholar 

  31. Schmidt V.V., Mkrchyan G.S. (1974). Sov. Phys. Usp. 17: 170

    Article  ADS  Google Scholar 

  32. V. V. Schmidt, J. Ekspt. Teoret. Fiz. 61, 398 (1971) [Sov. Phys. JETP 34, 211 (1972)].

  33. Van de Vondel J., de Souza Silva C.C., Zhu B.Y., Morello M., Moshchalkov V.V.(2005). Phys. Rev. Lett. 94: 057003

    Article  ADS  Google Scholar 

  34. Berdiyorov G.R., Cabral L.R.E., Peeters F.M. (2005). J. Math. Phys. 46: 095105

    Article  MathSciNet  Google Scholar 

  35. Schweigert V.A., Peeters F.M. (1999). Phys. Rev. Lett. 83: 2409

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Theoretical Physics, Atomic Energy Authority, P.O. Box 9516, Nasr City, Cairo, Egypt

    L. N. Shehata & A. Y. Afram

Authors
  1. L. N. Shehata
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Y. Afram
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to L. N. Shehata.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Shehata, L.N., Afram, A.Y. Vortex Interaction with Mesoscopic Surface Cavities in Superconductors. J Low Temp Phys 147, 601–613 (2007). https://doi.org/10.1007/s10909-007-9339-4

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10909-007-9339-4

Keywords

Search

Navigation