Skip to main content
SpringerLink
Log in

Coexistence of Vortex Liquid and Solid in Rotating Bose-Einstein Condensate

  • Original Article
  • Published:
Journal of Low Temperature Physics Aims and scope Submit manuscript

No Heading

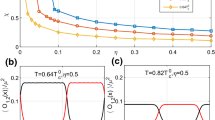
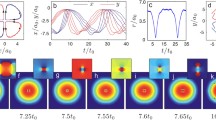
We perform computer simulations for the Gross-Pilaevskii equation with a tiny damping in order to study the condensate wave-function in 3-D rotating Bose-Einstein condensate under the trapping potential. We find that the wave-function is divided into two kinds of phases in terms of its coherent feature. The first one is a coherent phase which is characterized by the static vortex lattice located close to the center of the trapping potential, and the second one is an incoherent one which lies outside the first coherent phase and shows vortex liquid like behaviors. The boundary between the two phases is quite sharp like the phase interface as seen in the first-order phase transition. This result suggests that the melting seen in type II superconductors spatially occurs in the rotating Bose-Einstein condensate since the wave-function amplitude decreases with departing from the center of the trap and its coherent feature is overcome by intrinsic fluctuations at a certain distance.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. 1. K.W.Madison, F. Chevy, V.Bretin, and D.Dalibard, Phys. Rev. Lett., 86, 4443(2001).

    Google Scholar 

  2. 2. P.C.Haljan, I.Coddington, P.Engels, and E.A.Cornell, Phys.Rev.Lett., 87, 210403(2001).

    Google Scholar 

  3. 3. C.Raman, J.R.Abo-Shaeer, J.M.Vogels, K.Xu, and W.Ketterle, Phys.Rev.Lett., 87, 210402(2001).

    Google Scholar 

  4. 4. M.Tsubota, K.Kasamatsu, and M.Ueda, Phys.Rev.A 65, 023603 (2002).

    Google Scholar 

  5. 5. A.A.Penckwitt, R.J.Ballagh, and C.W.Gardiner, Phys.Rev.Lett., 89, 260402(2002).

    Google Scholar 

  6. 6. G.Blatter, M.V.Feigelman, V.B.Geshkenbein, A.I.Larkin, and V.M.Vinokur, Rev.Mod.Phys., 66, 1125(1994).

    Google Scholar 

  7. 7. M.Machida, A.Tanaka, and M.Tachiki, Physica C 288, 199(1997).

    Google Scholar 

  8. 8. B.M.Herbst, F.Varadi, and M.J.Ablowitz, Math. Comput. Simulation 37, 353(1994).

    Google Scholar 

  9. 9. T.B.Taha and M.J.Ablowitz, J. Comp. Phys., 55, 203 (1984).

    Google Scholar 

  10. 10. D.A.Butts and D.S.Rokhsar, Nature, 397, 327(1999).

    Google Scholar 

  11. 11. C.Lobo, A.Sinatra, and Y.Castin, Phys.Rev.Lett., 92, 020403(2004).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. CCSE, Japan Atomic Energy Research Institute, 6-9-3 Higashi-Ueno, 110-0015, Taito-ku, Tokyo

    Masahiko Machida & Narimasa Sasa

  2. Institute of Physics, University of Tsukuba, 1-1-1 Tennodai, 305-8571, Tsukuba, Ibaraki, Japan

    Hideki Matsumoto

Authors
  1. Masahiko Machida
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Narimasa Sasa
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hideki Matsumoto
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

PACS numbers: 03.75.Lm, 03.75.Kk, 74.25.Qt, 74.40.+k

Rights and permissions

Reprints and permissions

About this article

Cite this article

Machida, M., Sasa, N. & Matsumoto, H. Coexistence of Vortex Liquid and Solid in Rotating Bose-Einstein Condensate. J Low Temp Phys 138, 623–628 (2005). https://doi.org/10.1007/s10909-005-2271-6

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10909-005-2271-6

Keywords

Search

Navigation