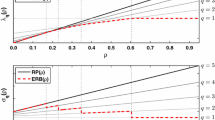
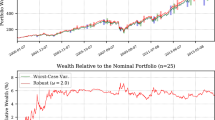
Abstract
The risk parity solution to the asset allocation problem yields portfolios where the risk contribution from each asset is made equal. We consider a generalized approach to this problem. First, we set an objective that seeks to maximize the portfolio expected return while minimizing portfolio risk. Second, we relax the risk parity condition and instead bound the risk dispersion of the constituents within a predefined limit. This allows an investor to prescribe a desired risk dispersion range, yielding a portfolio with an optimal risk–return profile that is still well-diversified from a risk-based standpoint. We add robustness to our framework by introducing an ellipsoidal uncertainty structure around our estimated asset expected returns to mitigate estimation error. Our proposed framework does not impose any restrictions on short selling. A limitation of risk parity is that allowing of short sales leads to a non-convex problem. However, we propose an approach that relaxes our generalized risk parity model into a convex semidefinite program. We proceed to tighten this relaxation sequentially through the alternating direction method of multipliers. This procedure iterates between the convex optimization problem and the non-convex problem with a rank constraint. In addition, we can exploit this structure to solve the non-convex problem analytically and efficiently during every iteration. Numerical results suggest that this algorithm converges to a higher quality optimal solution when compared to the competing non-convex problem, and can also yield a higher ex post risk-adjusted rate of return.




Similar content being viewed by others
Notes
Short selling pertains to taking negative positions on our investments. ‘Long-only’ refers to portfolios where we can only take non-negative positions.
An estimated covariance matrix of financial assets has the useful property of being symmetric and positive semidefinite, provided sufficient data is used for estimation.
References
Bai, X., Scheinberg, K., Tütüncü, R.H.: Least-squares approach to risk parity in portfolio selection. Quantitative Finance 16(3), 357–376 (2016)
Best, M.J., Grauer, R.R.: On the sensitivity of mean-variance-efficient portfolios to changes in asset means: some analytical and computational results. Rev. Financ. Stud. 4(2), 315–342 (1991)
Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J., et al.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends ® in Mach. Learn. 3(1), 1–122 (2011)
Broadie, M.: Computing efficient frontiers using estimated parameters. Ann. Oper. Res. 45(1), 21–58 (1993)
Bruder, B., Roncalli, T., et al.: Managing Risk Exposures Using the Risk Budgeting Approach. Tech. rep., University Library of Munich, Germany (2012)
Chen, G., Teboulle, M.: A proximal-based decomposition method for convex minimization problems. Math. Program. 64(1–3), 81–101 (1994)
Chopra, V.K., Ziemba, W.T.: The effect of errors in means, variances, and covariances on optimal portfolio choice. J. Portf. Manag. 19(2), 6–11 (1993)
Costa, G., Kwon, R.H.: Risk parity portfolio optimization under a markov regime-switching framework. Quant. Finance 19(3), 453–471 (2019)
Delage, E., Ye, Y.: Distributionally robust optimization under moment uncertainty with application to data-driven problems. Oper. Res. 58(3), 595–612 (2010)
Dunning, I., Huchette, J., Lubin, M.: Jump: a modeling language for mathematical optimization. Soc. Ind. Appl. Math. 59(2), 295–320 (2017). https://doi.org/10.1137/15M1020575
Eckstein, J., Bertsekas, D.P.: On the Douglas–Rachford splitting method and the proximal point algorithm for maximal monotone operators. Math. Program. 55(1–3), 293–318 (1992)
Eckstein, J., Fukushima, M.: Some reformulations and applications of the alternating direction method of multipliers. In: Hager, W.W., Hearn, D.W., Pardalos, P.M. (eds.) Large Scale Optimization, pp. 115–134. Springer, Boston (1994)
Fabozzi, F.J., Kolm, P.N., Pachamanova, D.A., Focardi, S.M.: Robust portfolio optimization. J. Portf. Manag. 33(3), 40 (2007)
Fama, E.F., French, K.R.: Common risk factors in the returns on stocks and bonds. J. Financ. Econ. 33(1), 3–56 (1993)
Feng, Y., Palomar, D.P.: SCRIP: Successive convex optimization methods for risk parity portfolio design. IEEE Trans. Signal Process. 63(19), 5285–5300 (2015)
Fortin, M., Glowinski, R.: On decomposition-coordination methods using an augmented Lagrangian. In: Fortin, M., Glowinski, R. (eds.) Augmented Lagrangian Methods: Applications to the Solution of Boundary-Value Problems, vol. 15. Elsevier, Amsterdam (1983)
Fukushima, M.: Application of the alternating direction method of multipliers to separable convex programming problems. Comput. Optim. Appl. 1(1), 93–111 (1992)
Gabay, D.: Applications of the method of multipliers to variational inequalities. In: Fortin, M., Glowinski, R. (eds.) Augmented Lagrangian Methods: Applications to the Solution of Boundary-Value Problems, vol. 15, pp. 299–331. Elsevier, Amsterdam (1983)
Gabay, D., Mercier, B.: A dual algorithm for the solution of non linear variational problems via finite element approximation. Institut de recherche d’informatique et d’automatique 2, 17–40 (1975)
Ghadimi, E., Teixeira, A., Shames, I., Johansson, M.: Optimal parameter selection for the alternating direction method of multipliers (ADMM): quadratic problems. IEEE Trans. Autom. Control 60(3), 644–658 (2015)
Glowinski, R., Marroco, A.: Sur l’approximation, par éléments finis d’ordre un, et la résolution, par pénalisation-dualité d’une classe de problèmes de dirichlet non linéaires. Revue française d’automatique, informatique, recherche opérationnelle. Analyse numérique 9, 41–76 (1975)
Goldfarb, D., Iyengar, G.: Robust portfolio selection problems. Math. Oper. Res. 28(1), 1–38 (2003)
Goldstein, T., O’Donoghue, B., Setzer, S., Baraniuk, R.: Fast alternating direction optimization methods. SIAM J. Imaging Sci. 7(3), 1588–1623 (2014)
Haugh, M., Iyengar, G., Song, I.: A generalized risk budgeting approach to portfolio construction. J. Comput. Finance 21(2), 29–60 (2017)
He, B., Yang, H., Wang, S.: Alternating direction method with self-adaptive penalty parameters for monotone variational inequalities. J. Optim. Theory Appl. 106(2), 337–356 (2000)
Jorion, P.: Bayes-Stein estimation for portfolio analysis. J. Financ. Quant. Anal. 21(3), 279–292 (1986)
Kapsos, M., Christofides, N., Rustem, B.: Robust risk budgeting. Ann. Oper. Res. 266, 1–23 (2017)
Ledoit, O., Wolf, M.: Improved estimation of the covariance matrix of stock returns with an application to portfolio selection. J. Empir. Finance 10(5), 603–621 (2003)
Lintner, J.: The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. Rev. Econ. Stat. 47, 13–37 (1965)
Lobo, M.S., Boyd, S.: The worst-case risk of a portfolio. Technical report. Available from http://web.stanford.edu/~boyd/papers/pdf/risk_bnd.pdf (2000)
Maillard, S., Roncalli, T., Teïletche, J.: The properties of equally weighted risk contribution portfolios. J. Portf. Manag. 36(4), 60–70 (2010)
Markowitz, H.: Portfolio selection. J. Finance 7(1), 77–91 (1952)
Merton, R.C.: On estimating the expected return on the market: an exploratory investigation. J. Financ. Econ. 8(4), 323–361 (1980)
Mossin, J.: Equilibrium in a capital asset market. Econom. J. Econom. Soc. 34, 768–783 (1966)
Nesterov, Y.: Introductory Lectures on Convex Optimization: A Basic Course, vol. 87. Springer, New York (2013)
Qian, E.: Risk parity portfolios: Efficient portfolios through true diversification. Panagora Asset Management White Paper (2005)
Qian, E.: On the financial interpretation of risk contribution: risk budgets do add up. J. Invest. Manag. 4(4), 41–51 (2006)
Quandl.com: Wiki—various end-of-day stock prices (2017). https://www.quandl.com/databases/WIKIP/usage/export. [Online; Accessed 07-Nov-2017]
Raghunathan, A.U., Di Cairano, S.: Alternating direction method of multipliers for strictly convex quadratic programs: Optimal parameter selection. In: American Control Conference (ACC), pp. 4324–4329. IEEE (2014)
Sharpe, W.F.: Capital asset prices: a theory of market equilibrium under conditions of risk. J. Finance 19(3), 425–442 (1964)
Sharpe, W.F.: The sharpe ratio. J. Portf. Manag. 21(1), 49–58 (1994)
Tseng, P.: Applications of a splitting algorithm to decomposition in convex programming and variational inequalities. SIAM J. Control Optim. 29(1), 119–138 (1991)
Tütüncü, R.H., Koenig, M.: Robust asset allocation. Ann. Oper. Res. 132(1–4), 157–187 (2004)
Wang, S., Liao, L.: Decomposition method with a variable parameter for a class of monotone variational inequality problems. J. Optim. Theory Appl. 109(2), 415–429 (2001)
You, S., Peng, Q.: A non-convex alternating direction method of multipliers heuristic for optimal power flow. In: 2014 IEEE International Conference on Smart Grid Communications (SmartGridComm), pp. 788–793. IEEE (2014)
Funding
Funding was provided by Natural Sciences and Engineering Research Council of Canada (Grant Number 455963).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Costa, G., Kwon, R.H. Generalized risk parity portfolio optimization: an ADMM approach. J Glob Optim 78, 207–238 (2020). https://doi.org/10.1007/s10898-020-00915-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10898-020-00915-x