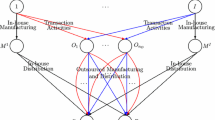
Abstract
In this paper, we develop a multitiered competitive supply chain network game theory model, which includes the supplier tier. The firms are differentiated by brands and can produce their own components, as reflected by their capacities, and/or obtain components from one or more suppliers, who also are capacitated. The firms compete in a Cournot–Nash fashion, whereas the suppliers compete a la Bertrand since firms are sensitive to prices. All decision-makers seek to maximize their profits with consumers reflecting their preferences through the demand price functions associated with the demand markets for the firms’ products. We construct supply chain network performance measures for the full supply chain and the individual firm levels that assess the efficiency of the supply chain or firm, respectively, and also allow for the identification and ranking of the importance of suppliers as well as the components of suppliers with respect to the full supply chain or individual firm. The framework is illustrated through a series of numerical supply chain network examples.



Similar content being viewed by others
References
Bertrand, J.: Theorie mathematique de la richesse sociale. Journal des Savants, 67, 499–508 (1883)
Bertsekas, D.P., Tsitsiklis, J.N.: Parallel and Distributed Computation—Numerical Methods. Prentice Hall, Englewood Cliffs, New Jersey (1989)
Chen, Z., Teng, C., Zhang, D., Sun, J.: Modelling inter-supply chain competition with resource limitation and demand disruption. Int. J. Syst. Sci. (2014). doi:10.1080/00207721.2014.942499
Chopra, S., Sodhi, M.S.: Managing risk to avoid supply-chain breakdown. MIT Sloan Manag. Rev. 46(1), 53–61 (2004)
Clendon, L., Bird, L.: 5th Annual Survey Supply Chain Resilience. Business Continuity Institute, Caversham, United Kingdom (2013)
Cournot, A.A.: Researches into the Mathematical Principles of the Theory of Wealth, English translation. MacMillan, London, England (1838)
Cruz, J.M.: Dynamics of supply chain networks with corporate social responsibility through integrated environmental decision-making. Eur. J. Oper. Res. 184, 1005–1031 (2008)
Cruz, J.M.: The effects of network relationships on global supply chain vulnerability. In: Wu, T., Blackhurst, J. (eds.) Managing Supply Chain Risk and Vulnerability: Tools and Methods for Supply Chain Decision Makers, pp. 113–140. Springer, Berlin, Germany (2011)
Cruz, J.M., Nagurney, A., Wakolbinger, T.: Financial engineering of the integration of global supply chain networks and social networks with risk management. Nav. Res. Logist. 53, 674–696 (2006)
Dupuis, P., Nagurney, A.: Dynamical systems and variational inequalities. Ann. Oper. Res. 44, 9–42 (1993)
Gabay, D., Moulin, H.: On the uniqueness and stability of Nash equilibria in noncooperative games. In: Bensoussan, A., Kleindorfer, P., Tapiero, C.S. (eds.), Applied Stochastic Control in Econometrics and Management Science. North-Holland, Amsterdam, The Netherlands, pp. 271-294 (1980)
Gupta, D.: The \((Q, r)\) inventory system with an unreliable supplier. INFOR 34, 59–76 (1996)
Kinderlehrer, D., Stampacchia, G.: An Introduction to Variational Inequalities and their Applications. Academic Press, New York (1980)
Lee, D., Pierson, D.: Disaster in Japan exposes supply chain flaw. Los Angeles Times, (2011)
Liu, Z., Cruz, J.M.: Supply chain networks with corporate financial risks and trade credits under economic uncertainty. Int. J. Prod. Econ. 137, 55–67 (2012)
Liu, Z., Nagurney, A.: An integrated electric power supply chain and fuel market network framework: theoretical modeling with empirical analysis for New England. Nav. Res. Logist. 56, 600–624 (2006)
Liu, Z., Nagurney, A.: Supply chain networks with global outsourcing and quick-response production under demand and cost uncertainty. Ann. Oper. Res. 208(1), 251–289 (2013)
Mukherjee, A.S.: The Spider’s Strategy: Creating Networks to Avert Crisis, Create Change, and get Ahead. FT Press, Upper Saddle River, New Jersey (2008)
Nagurney, A.: Network Economics: A Variational Inequality Approach. Kluwer Academic Publishers, Dordrecht, The Netherlands (1999)
Nagurney, A.: Supply Chain Network Economics: Dynamics of Prices, Flows, and Profits. Edward Elgar Publishing, Cheltenham, England (2006)
Nagurney, A.: Formulation and analysis of horizontal mergers among oligopolistic firms with insights into the merger paradox: a supply chain network perspective. Comput. Manag. Sci. 7, 377–410 (2010)
Nagurney, A., Cruz, J., Dong, J., Zhang, D.: Supply chain networks, electronic commerce, and supply side and demand side risk. Eur. J. Oper. Res. 26, 120–142 (2005)
Nagurney, A., Dhanda, K.K.: Marketable pollution permits in oligopolistic markets with transaction costs. Oper. Res. 48(3), 424–435 (2000)
Nagurney, A., Dong, J., Zhang, D.: A supply chain network equilibrium model. Transp. Res. E 38, 281–303 (2002)
Nagurney, A., Dupuis, P., Zhang, D.: A dynamical systems approach for network oligopolies and variational inequalities. Ann. Reg. Sci. 28, 263–283 (1994)
Nagurney, A., Li, D.: A supply chain network game theory model with product differentiation, outsourcing of production and distribution, and quality and price competition. Ann. Oper. Res. 228(1), 479–503 (2015)
Nagurney, A., Li, D., Nagurney, L.S.: Pharmaceutical supply chain networks with outsourcing under price and quality competition. Int. Trans. Oper. Res. 20(6), 859–888 (2013)
Nagurney, A., Qiang, Q.: A network efficiency measure with application to critical infrastructure networks. J. Glob. Optim. 40, 261–275 (2008)
Nagurney, A., Qiang, Q.: Fragile Networks: Identifying Vulnerabilities and Synergies in an Uncertain World. Wiley, Hoboken, New Jersey (2009)
Nagurney, A., Zhang, D.: Projected Dynamical Systems and Variational Inequalities with Applications. Kluwer Academic Publishers, Boston, Massachusetts (1996)
Nash, J.F.: Equilibrium points in n-person games. Proc. Natl. Acad. Sci. USA 36, 48–49 (1950)
Nash, J.F.: Noncooperative games. Ann. Math. 54, 286–298 (1951)
Parlar, M.: Continuous review inventory problem with random supply interruptions. Eur. J. Oper. Res. 99, 366–385 (1997)
Parlar, M., Perry, D.: Inventory models of future supply uncertainty with single and multiple suppliers. Nav. Res. Logist. 43, 191–210 (1996)
Payne, J.W., Bettman, J.R., Luce, M.F.: When time is money: decision behavior under opportunity-cost time pressure. Organ. Behav. Hum. Decis. Process. 66(2), 131–152 (1996)
Qiang, Q.: The closed-loop supply chain network with competition and design for remanufactureability. J. Clean. Prod. 105, 346–356 (2015)
Qiang, Q., Ke, K., Anderson, T., Dong, J.: The closed-loop supply chain network with competition, distribution channel investment, and uncertainties. Omega 41(2), 186–194 (2013)
Qiang, Q., Nagurney, A.: A bi-criteria indicator to assess supply chain network performance for critical needs under capacity and demand disruptions. Transp. Res. A 46(5), 801–812 (2012)
Qiang, Q., Nagurney, A., Dong, J.: Modeling of supply chain risk under disruptions with performance measurement and robustness analysis. In: Wu, T., Blackhurst, J. (eds.) Managing Supply Chain Risk and Vulnerability: Tools and Methods for Supply Chain Decision Makers, pp. 91–111. Springer, Berlin, Germany (2009)
Sandoval-Chavez, D.A., Beruvides, M.G.: Using opportunity costs to determine the cost of quality: a case study in a continuous-process industry. Eng. Econ. 43, 107–124 (1998)
Stevenson, A., Lindberg, C.A. (eds.): New Oxford American Dictionary, 3rd edn. Oxford University Press, England (2010)
Tang, C.S., Zimmerman, J.D., Nelson, J.I.: Managing new product development and supply chain risks: The Boeing 787 case. Supply Chain Forum 10(2), 74–86 (2009)
Tomlin, B.T.: On the value of mitigation and contingency strategies for managing supply chain disruption risks. Manag. Sci. 52, 639–657 (2006)
Toyasaki, F., Daniele, P., Wakolbinger, T.: A variational inequality formulation of equilibrium models for end-of-life products with nonlinear constraints. Eur. J. Oper. Res. 236, 340–350 (2014)
Wu, T., Blackhurst, J. (eds.): Managing Supply Chain Risk and Vulnerability: Tools and Methods for Supply Chain Decision Makers. Springer, Berlin, Germany (2009)
Wu, T., Blackhurst, J., Chidambaram, V.: The model for inbound supply risk analysis. Comput. Ind. 57, 350–365 (2006)
Yang, J.: Worst Thai floods in 50 years hit Apple, Toyota supply chain. Bloomberg (2011)
Acknowledgments
This research was supported by the National Science Foundation (NSF) Grant CISE #1111276, for the NeTS: Large: Collaborative Research: Network Innovation Through Choice project awarded to the University of Massachusetts Amherst. This support is gratefully acknowledged. The authors acknowledge two anonymous reviewers and the Editor for their careful reading of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Li, D., Nagurney, A. Supply chain performance assessment and supplier and component importance identification in a general competitive multitiered supply chain network model. J Glob Optim 67, 223–250 (2017). https://doi.org/10.1007/s10898-015-0371-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10898-015-0371-7