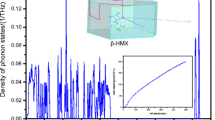
An analysis of the existing approximations used for describing the dependence of heat capacity at a constant volume on the temperature of a molecular crystal has been carried out. It is shown that the considered Debye and Einstein approximations do not enable one to adequately describe the dependence of heat capacity at a constant volume on the temperature of the molecular crystals of nitro compounds. This inference requires the development of special approximations that would describe both low-frequency and high-frequency parts of the vibrational spectra of molecular crystals. This work presents a universal dependence allowing one to describe the dependence of heat capacity at a constant volume on temperature for a number of molecular crystals of nitro compounds.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. N. Zharkov and V. A. Kalinin, Equations of State at High Temperatures and Pressures [in Russian], Nauka, Moscow (1968).
Yu. M. Kovalev, Equations of state and of the temperature of shock compression of crystalline explosives, Fiz. Goreniya Vzryva, 20, No. 2, 102–107 (1984).
Yu. M. Kovalev, Mathematical simulation of the thermal component of the equation of state of molecular crystals, Vestn. Yuzhno-Uralsk. Gos. Univ., 6, No. 1, 34−42 (2013).
V. F. Kuropatenko, Models of the Continuous Medium Mechanics [in Russian], Izd. Chelyabinsk. Gos. Univ., Chelyabinsk (2007).
V. F. Kuropatenko, Equations of state in mathematical models of the mechanics and physics, Mat. Modelir., 4, No. 12, 112−136 (1992).
D. Stall, E. Westram, and G. Zinke, The Chemical Thermophysics of Organic Compounds [Russian translation], Mir, Moscow (1971).
N. B. Vargaftik, Handbook of Thermotechnical Properties of Gases and Liquids [in Russian], Nauka, Moscow (1972).
Tsyan Sye-sen, Physical Mechanics [Russian translation], Mir, Moscow (1965).
V. G. Shchetinin, Calculation of the heat capacity of organic substances in shock and detonation waves, Khim. Fiz., 18, No. 5, 90–95 (1999).
B. M. Dobrats and P. C. Crawford, LLNL Explosives Handbook. Properties of Chemical Explosives and Explosive Simulants, University of California, Livermore, California (1985).
T. R. Gibbs and A. Popolato, Last Explosive Property Data. Los Alamos Series on Dynamic Material Properties, University of California Press, Berkeley−Los Angeles−London (1980).
L. A. Girifalco, Statistical Physics of the Solid [Russian translation], Mir, Moscow (1975).
A. I. Kitaigorodskii, Molecular Crystals [in Russian], Nauka, Moscow (1971).
Yu. M. Kovalev and A. V. Belik, Determination of the thermal component of the equation of state of molecular crystals, Chelyabinsk. Fiz.-Mat. Zh., No. 9 (300), 5−10 (2013).
T. Clark, Handbook of Computational Chemistry [Russian translation], Mir, Moscow (1990).
N. F. Stepanov and Yu. V. Novakovskaya, Quantum chemistry today, Ross. Khim. Zh., LI, No. 5, 5–17 (2007).
P. J. Miller, S. Block, and G. J. Piermarini, Effect of pressure on the vibration spectra of liquid nitromethane. J. Phys. Chem., 93, 462–466 (1989).
Author information
Authors and Affiliations
Corresponding author
Additional information
V. F. Kuropatenko is deceased.
Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 91, No. 2, pp. 297–306, March–April, 2018.
Rights and permissions
About this article
Cite this article
Kovalev, Y.M., Kuropatenko, V.F. Determination of the Temperature Dependence of Heat Capacity for Some Molecular Crystals of Nitro Compounds. J Eng Phys Thermophy 91, 278–287 (2018). https://doi.org/10.1007/s10891-018-1747-6
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10891-018-1747-6