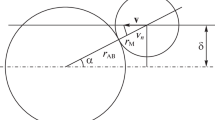
Unsteady nonisothermal traverse flow of an impurity-containing viscous fluid past a rotating circular cylinder has been investigated with account of the mechanical and thermal interaction of the carrier and dispersed phases. The processes occurring have been described mathematically with the Lagrange approach. The influence of the impurity on the flow pattern has been analyzed; the dependences of the drag coefficient, the lifting-force amplitude, and the Nusselt number of the cylinder on the relative rotational velocity of its surface have been determined.
Similar content being viewed by others
References
N. Ya. Fabrikant (ed.), Current State of the Hydroaerodynamics of a Viscous Fluid. Review of Theories and Experimental Works on the Problems of a Boundary Layer, Turbulent Motion, and Motion in a Wake [in Russian], Vol. 1, Gos. Izd. IL, Moscow (1948).
N. Ya. Fabrikant, Aerodynamics. A General Course [in Russian], Nauka, Moscow(1964).
L. A. Dorfman, Hydrodynamic Resistance and Heat Transfer of Rotating Bodies [in Russian], Gos. Izd. Fiz.-Mat. Lit., Moscow (1960).
S. S. Kutateladze, Heat Transfer and Hydrodynamic Resistance: A Reference Book [in Russian], Énergoatomizdat, Moscow (1990).
G. H. Hu, D. J. Sun, X. Y. Yin, and B. G. Tong, Hopf bifurcation in wake behind a rotating and translating circular cylinder, Phys. Fluids, 8, No. 7, 1972–1974 (1996).
S. Kang, H. Choi, and S. Lee, Laminar flow past circular cylinder, Phys. Fluids, 11, No. 11, 3312–3321 (1999).
F. J. Barnes, Vortex shedding in the wake if a rotating circular cylinder at low Reynolds numbers, J. Phys. D: Appl. Phys., No. 33, 141–144 (2000).
D. Stojkovic, M. Breuer, and F. Durst, Effect of high rotation rates on the laminar flow around a circular cylinder, Phys. Fluids, 14, No. 9, 3160–3178 (2002).
S. Mittal and B. Kumar, Flow past a rotating cylinder, J. Fluid Mech., 476, 303–334 (2003).
I. V. Morenko and A. B. Mazo, Numerical simulation of the viscosity of the separated flow past a rotating circular, in: Proc. Second Int. Summer Scientific School "High Speed Hydrodynamics," June 27–July 3 2004, Cheboksary (2004), pp. 307–311.
A. B. Mazo and I. V. Morenko, Interaction of a viscous-fluid flow and a rotating circular cylinder, in: Continuum-Mechanics Models. Proc. N. I. Lobachevskii Math. Center [in Russian], Vol. 27, Izd. Kazansk. Matem. Obshch., Kazan (2004), pp. 161–171.
R. Akoury, M. Braza, R. Perrin, et al., The three-dimensional transition in the flow around a rotating cylinder, J. Fluid Mech., 607, 1–11 (2008).
Y. T. Yan and Y. Q. Zu, Numerical simulation of heat transfer and fluid flow past a rotating isothermal cylinder — A LBM approach, Int. J. Heat Mass Transf., No. 51, 2519–2536 (2008).
J. Ghazanfarian and M. R. H. Nobari, A numerical study of convective heat transfer from a rotating cylinder with crossflow oscillation, Int. J. Heat Mass Transf., No. 52, 5402–5411 (2009).
A. A. Prikhod′ko and D. A. Redchits, Numerical simulation of unsteady detached flow of an incompressible viscous fluid past a rotating cylinder, Izv. Ross. Akad. Nauk, Mekh. Zhidk. Gaza, No. 6, 32–39 (2009).
R. I. Nigmatulin, Dynamics of Multiphase Media [in Russian], Part I, Nauka, Moscow (1987).
A. N. Volkov and Yu. M. Tsirkunov, Influence of a dispersed impurity on the structure of an unsteady two-phase wake of the cylinder in transverse flow at moderate Reynolds numbers, Mat. Model., 15, No. 7, 98–110 (2003).
I. V. Morenko and V. L. Fedyaev, Peculiaritiesoftwo-phaseflowpastacylinder, Ékol. Vestn. Nauch. Tsentr. Chernomorsk. Ékon. Sotr., No. 4, 52–58 (2010).
I. V. Morenko and V. L. Fedyaev, Nonisothermalflow of a monodisperse mixture past a circular cylinder, Teplov. Protsessy Tekh., 3, No. 6, 242–252 (2011).
G. F. Al-Sumaily, A. Nakayama, J. Sheridan, and M. C. Thompson, The effect of porous media particle size on forced convection from a circular cylinder without assuming local thermal equilibrium between phases, Int. J. Heat Mass Transf., No. 55, 3366–3378 (2012).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 87, No. 3, pp. 549–555, May–June, 2014.
Rights and permissions
About this article
Cite this article
Morenko, I.V., Fedyaev, V.L. Laminar Nonisothermal Flow of a Viscous Fluid with Solid Particles Past a Rotating Circular Cylinder. J Eng Phys Thermophy 87, 566–572 (2014). https://doi.org/10.1007/s10891-014-1046-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10891-014-1046-9