Skip to main content
SpringerLink
Log in

On localization of contact surfaces in multifluid hydrodynamics

  • Published:
Journal of Engineering Physics and Thermophysics Aims and scope

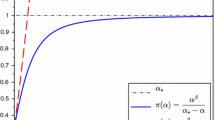
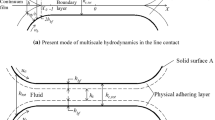
Within the framework of the unified-equilibrium model of a multicomponent mixture that accounts for the forces of interfractional interaction, the problem of localization of contact surfaces is solved numerically in Euler variables. A finite-volume conservative scheme with the approximate Riemann solver HLLC was used in the calculations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J. Glimm, J. Grove, X. Li, and D. Tan, Robust computational algorithms for dynamic interface tracking in three dimensions, SIAM J. Sci. Comput., 21, No. 6, 2240–2276 (2000).

    Article  MATH  MathSciNet  Google Scholar 

  2. R. Scardovelli and S. Zaleski, Direct numerical simulation of free-surface and interfacial flow, Annu. Rev. Fluid Mech., 31, 567–598 (1999).

    Article  MathSciNet  Google Scholar 

  3. S. Osher and R. P. Fedkiw, A level set method: An overview and some recent results, J. Comput. Phys., 169, 463–502 (2001).

    Article  MATH  MathSciNet  Google Scholar 

  4. S. M. Bakhrakh, Yu. P. Glagoleva, M. S. Samigulin, et al., Calculation of gasdynamic flows based on the method of concentrations, Dokl. Akad. Nauk SSSR, 257, No. 3, 566–569 (1981).

    Google Scholar 

  5. Yu. A. Bondarenko and Yu. V. Yanilkin, Calculation of the thermodynamic parameters of mixed cells in gas dynamics, Mat. Modelir., 15, No. 6, 63–81 (2002).

    Google Scholar 

  6. R. Abgrall and S. Karni, Computations of compressible multifluids, J. Comput. Phys., 169, 594–623 (2001).

    Article  MATH  MathSciNet  Google Scholar 

  7. Keh-Ming Shyue, A fluid-mixture type algorithm for compressible multicomponent flow with Van der Waals equation of state, J. Comput. Phys., 156, 43–88 (1999).

    Article  MATH  MathSciNet  Google Scholar 

  8. Keh-Ming Shyue, A fluid-mixture type algorithm for compressible multicomponent flow with Mie–Gruneisen equation of state, J. Comput. Phys., 171, 678–707 (2001).

    Article  MATH  MathSciNet  Google Scholar 

  9. I. É. Ivanov and I. A. Kryukov, Numerical simulation of flows of a multicomponent gas with strong discontinuities of the mixture properties, Mat. Modelir., 19, No. 12, 89–100 (2007).

    MathSciNet  Google Scholar 

  10. G. Allaire, S. Clerc, and S. Kokh, A five-equation model for the simulation of interfaces between compressible fluids, J. Comput. Phys., 181, 577–616 (2002).

    Article  MATH  MathSciNet  Google Scholar 

  11. A. Murrone and H. Guillard, A five-equation reduced model for compressible two-phase flow problems, J. Comput. Phys., 202, 664–698 (2005).

    Article  MATH  MathSciNet  Google Scholar 

  12. V. S. Surov, Single-velocity model of a heterogeneous medium with a hyperbolic adiabatic core, Zh. Vych. Mat. Mat. Fiz., 48, No. 6, 1111–1125 (2008).

    MATH  Google Scholar 

  13. A. G. Kulikovskii, N. V. Pogorelov, and A. Yu. Semenov, Mathematical Problems of Numerical Solution of Hyperbolic Systems of Equations [in Russian], Fizmatlit, Moscow (2001).

    Google Scholar 

  14. V. S. Surov, Concerning a means of approximate solution of the Riemann problem for a single-velocity multicomponent mixture, Inzh.-Fiz. Zh., 83, No. 2, 351–356 (2010).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. South Urals State University, 76 Lenin Ave., Chelyabinsk, 454080, Russia

    V. S. Surov

Authors
  1. V. S. Surov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. S. Surov.

Additional information

Translated from Inzhenerno-Fizicheskii Zhurnal, Vol. 83, No. 3, pp. 518–527, May–June, 2010.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Surov, V.S. On localization of contact surfaces in multifluid hydrodynamics. J Eng Phys Thermophy 83, 549–559 (2010). https://doi.org/10.1007/s10891-010-0376-5

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10891-010-0376-5

Keywords

Search

Navigation