Abstract
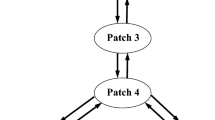
In this paper, we show the existence of a Hopf bifurcation in a delayed single population model with patch structure. The effect of the dispersal rate on the Hopf bifurcation is considered. Especially, if each patch is favorable for the species, we show that when the dispersal rate tends to zero, the limit of the Hopf bifurcation value is the minimum of the “local” Hopf bifurcation values over all patches. On the other hand, when the dispersal rate tends to infinity, the Hopf bifurcation value tends to that of the “average” model.







Similar content being viewed by others
References
Allen, L.J.S., Bolker, B.M., Lou, Y., Nevai, A.L.: Asymptotic profiles of the steady states for an SIS epidemic patch model. SIAM J. Appl. Math. 67(5), 1283–1309 (2007)
Busenberg, S., Huang, W.: Stability and Hopf bifurcation for a population delay model with diffusion effects. J. Differ. Equ. 124(1), 80–107 (1996)
Chen, S., Lou, Y., Wei, J.: Hopf bifurcation in a delayed reaction-diffusion-advection population model. J. Differ. Equ. 264(8), 5333–5359 (2018)
Chen, S., Shi, J.: Stability and Hopf bifurcation in a diffusive logistic population model with nonlocal delay effect. J. Differ. Equ. 253(12), 3440–3470 (2012)
Chen, S., Shi, J., Shuai, Z., Wu, Y.: Spectral monotonicity of perturbed quasi-positive matrices with applications in population dynamics (Submitted)
Chen, S., Wei, J., Zhang, X.: Hopf bifurcation for a delayed diffusive logistic population model in the advective heterogeneous environment. J. Dyn. Differ, Equ (2019)
Chen, S., Yu, J.: Stability and bifurcations in a nonlocal delayed reaction-diffusion population model. J. Differ. Equ. 260(1), 218–240 (2016)
Crandall, M.G., Rabinowitz, P.H.: Bifurcation from simple eigenvalues. J. Funct. Anal. 8, 321–340 (1971)
Guo, S.: Stability and bifurcation in a reaction-diffusion model with nonlocal delay effect. J. Differ. Equ. 259(4), 1409–1448 (2015)
Guo, S.: Spatio-temporal patterns in a diffusive model with non-local delay effect. IMA J. Appl. Math. 82(4), 864–908 (2017)
Guo, S., Yan, S.: Hopf bifurcation in a diffusive Lotka-Volterra type system with nonlocal delay effect. J. Differ. Equ. 260(1), 781–817 (2016)
Hale, J.: Theory of Functional Differential Equations. Applied Mathematical Sciences, vol. 3, 2nd edn. Springer, New York (1977)
Hu, R., Yuan, Y.: Spatially nonhomogeneous equilibrium in a reaction-diffusion system with distributed delay. J. Differ. Equ. 250(6), 2779–2806 (2011)
Kuang, Y.: Delay Differential Equations with Applications in Population Dynamics, volume 191 of Mathematics in Science and Engineering. Academic Press Inc, Boston (1993)
Liao, K.-L., Lou, Y.: The effect of time delay in a two-patch model with random dispersal. Bull. Math. Biol. 76(2), 335–376 (2014)
Lou, Y.: On the effects of migration and spatial heterogeneity on single and multiple species. J. Differ. Equ. 223(2), 400–426 (2006)
Memory, M.C.: Bifurcation and asymptotic behavior of solutions of a delay-differential equation with diffusion. SIAM J. Math. Anal. 20(3), 533–546 (1989)
Shi, Q., Shi, J., Song, Y.: Hopf bifurcation and pattern formation in a delayed diffusive logistic model with spatial heterogeneity. Discrete Contin. Dyn. Syst. Ser. B 24(2), 467–486 (2019)
Smith, H.L., Waltman, P.: The theory of the chemostat, volume 13 of Cambridge Studies in Mathematical Biology. Cambridge University Press, Cambridge (1995). Dynamics of microbial competition
Su, Y., Wei, J., Shi, J.: Hopf bifurcations in a reaction–diffusion population model with delay effect. J. Differ. Equ. 247(4), 1156–1184 (2009)
Su, Y., Wei, J., Shi, J.: Hopf bifurcation in a diffusive logistic equation with mixed delayed and instantaneous density dependence. J. Dyn. Differ. Equ. 24(4), 897–925 (2012)
Yan, X.-P., Li, W.-T.: Stability of bifurcating periodic solutions in a delayed reaction-diffusion population model. Nonlinearity 23(6), 1413–1431 (2010)
Yan, X.-P., Li, W.-T.: Stability and Hopf bifurcations for a delayed diffusion system in population dynamics. Discrete Contin. Dyn. Syst. Ser. B 17(1), 367–399 (2012)
Yoshida, K.: The Hopf bifurcation and its stability for semilinear diffusion equations with time delay arising in ecology. Hiroshima Math. J. 12(2), 321–348 (1982)
Zhao, X.-Q., Jing, Z.-J.: Global asymptotic behavior in some cooperative systems of functional-differential equations. Can. Appl. Math. Quart. 4(4), 421–444 (1996)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research is supported by the National Natural Science Foundation of China (No. 11771109) and Shandong Provincial Natural Science Foundation of China (No. ZR2020YQ01).
Rights and permissions
About this article
Cite this article
Chen, S., Shen, Z. & Wei, J. Hopf Bifurcation of a Delayed Single Population Model with Patch Structure. J Dyn Diff Equat 35, 1457–1487 (2023). https://doi.org/10.1007/s10884-021-09946-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10884-021-09946-8