Geometric Desingularization of a Cusp Singularity in Slow–Fast Systems with Applications to Zeeman’s Examples

Abstract

The cusp singularity—a point at which two curves of fold points meet—is a prototypical example in Takens’ classification of singularities in constrained equations, which also includes folds, folded saddles, folded nodes, among others. In this article, we study cusp singularities in singularly perturbed systems for sufficiently small values of the perturbation parameter, in the regime in which these systems exhibit fast and slow dynamics. Our main result is an analysis of the cusp point using the method of geometric desingularization, also known as the blow-up method, from the field of geometric singular perturbation theory. Our analysis of the cusp singularity was inspired by the nerve impulse example of Zeeman, and we also apply our main theorem to it. Finally, a brief review of geometric singular perturbation theory for the two elementary singularities from the Takens’ classification occurring for the nerve impulse example—folds and folded saddles—is included to make this article self-contained.

Appendices

Fenichel’s Theorem—Review

Consider a singularly perturbed equation

$$\begin{aligned} x'&=\varepsilon f(x,y) \nonumber \\ y'&=g(x,y), x\in \mathbb{R }^k, y\in \mathbb{R }^m, 0<\varepsilon \ll 1. \end{aligned}$$

Recall the constraining manifold (or critical manifold) $S_0$ defined by

$$\begin{aligned} S_0=\{(x,y) | g(x,y)=0\}. \end{aligned}$$

Suppose $\tilde{S}_0$ is an open subset of $S_0$. Then $\tilde{S}_0$ is normally hyperbolic if for every $(x,y)\in \mathrm{cl}\, (\tilde{S}_0)$ the matrix $D_y g$ has no eigenvalues on the imaginary axis.

Theorem 5

(Fenichel)[6, 7] If $\tilde{S}_0$ is normally hyperbolic then, for $\varepsilon >0$ and sufficiently small, there exists a locally invariant manifold $S_\varepsilon$ close to $\tilde{S}_0$ in the $C^1$ topology. The manifold $S_\varepsilon$ is diffeomorphic to $\tilde{S}_0$, and the flow on $S_\varepsilon$ is close to the flow of the reduced (constrained) equation on $\tilde{S}_0$.

Folds and Folded Saddles for $\varepsilon >0$—Review

1.1 Simple Folds

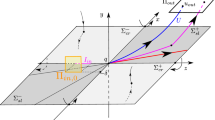
In this article, we need the description of the dynamics for folds with one fast and one slow variable (for the heartbeat model) and for folds with one fast and two slow variables (for the nerve impulse model). We begin by stating the result for the case of one slow variable and then introduce the theorem for two slow variables as its generalization. The result we state is Theorem 2.1 of [10]. We consider the equation

$$\begin{aligned}&x'=\varepsilon f(x, y, \varepsilon ), \nonumber \\&y'=g(x, y, \varepsilon ),\quad x,y \in \mathbb{R }\nonumber \\&\varepsilon '=0 \end{aligned}$$

(56)

and assume that

$$\begin{aligned} g(0, 0, 0)=0,\qquad \frac{\partial g}{\partial y} (0, 0, 0)=0. \end{aligned}$$

(57)

Further, we make non-degeneracy assumptions

$$\begin{aligned} \frac{\partial ^2 g}{\partial y^2}(0, 0, 0) \ne 0, \quad \frac{\partial g}{\partial x}(0, 0, 0) \ne 0, \quad f(0, 0, 0) \ne 0. \end{aligned}$$

(58)

In particular, we assume that

$$\begin{aligned} \frac{\partial ^2 g}{\partial y^2}(0, 0, 0) > 0, \quad \frac{\partial g}{\partial x}(0, 0, 0) > 0, \quad f(0,0,0)<0. \end{aligned}$$

These assumptions may be made without loss of generality, and the latter assumption determines that the direction of the flow is towards the fold (the fold point is a jump point). The information above is summarized in Fig. 19.

Fig. 19

Critical manifold, slow manifolds, and sections for a simple fold

We define the following sections of the flow:

$$\begin{aligned} \Sigma ^{in}=\{(\rho ^2, y), y\in R\} \end{aligned}$$

and

$$\begin{aligned} \Sigma ^{out}=\{(x, \rho ), x\in \mathbb{R }\} \end{aligned}$$

Also, we let $\Pi \, :\,\Sigma ^{in}\rightarrow \Sigma ^{out}$ be the transition map for the flow of (56).

Theorem 6

(simple fold with one slow variable) [10] For system (56) with assumptions (57) and (58), there exist $\varepsilon _0 >0$ and a neighborhood $U$ of $(0,0)$ such that the following assertions hold for $\varepsilon \in (0,\varepsilon _0]$:

• 1. The manifold $S_{a,\varepsilon }$ passes through $\Sigma ^{out}$ at a point $(h(\varepsilon ),\rho )$ where $h(\varepsilon ) = O(\varepsilon ^{2/3})$.

• 2. The transition map $\Pi \; : \Sigma ^{in}\cap U\rightarrow \Sigma ^{out}$ is a contraction with contraction rate $O(e^{-c/\varepsilon })$, where $c$ is a positive constant.

1.2 Simple Folds in Problems with Two Slow Dimensions

Consider the equation

$$\begin{aligned} x'&=\varepsilon f_1(x,y,z,\varepsilon ) \nonumber \\ y'&=\varepsilon f_2(x,y,z,\varepsilon ) \nonumber \\ z'&=g(x,y,z,\varepsilon ), x, y, z \in \mathbb{R }^1, 0<\varepsilon \ll 1. \end{aligned}$$

(59)

Let $S_0$ be the critical manifold, and define the fold line

$$\begin{aligned} F=\{(x,y,z)\in S_0 \; |\; \frac{\partial g}{\partial z}(x,y,z,0)\ne 0\}. \end{aligned}$$

Suppose that $(0,0,0)\in F$ and conditions (B) and (C) are satisfied. Further, we assume without loss of generality that

$$\begin{aligned} \frac{\partial ^2 g}{\partial z^2}(0,0,0,0) > 0, \quad \frac{\partial g}{\partial x}(0,0,0,0) > 0. \end{aligned}$$

(60)

We define the sections of the flow analogously as in the case of a simple fold. Namely, we introduce

$$\begin{aligned} \Sigma ^{in}=\{(x,y,z)\; | \; (x,y,z)=(\rho ^2, y, z), (y,z)\in \mathbb{R }^2\} \end{aligned}$$

and

$$\begin{aligned} \Sigma ^{out}=\{(x,y,z)\; | \; (x,y,z)=(x,y,\rho ), (x,y)\in \mathbb{R }^2\}. \end{aligned}$$

Theorem 7

(simple folds in problems with two slow variables) [14] For system (59) with the general nondegenracy conditions (A), (B), and (C), as well as with condition (60), there exist $\varepsilon _0 >0$ and a neighborhood $U$ of $(0,0,0)$ such that the following assertions hold for $\varepsilon \in (0,\varepsilon _0]$:

• (i) The transition map $\Pi \; :\; \Sigma ^{in}\cap U\rightarrow \Sigma ^{out}$ induced by the flow of (59) is a diffeomorphism mapping a neighborhood of $S_0\cap U$ into $\Sigma ^{out}$. Any trajectory starting at $S_{a,\varepsilon }\cap \Sigma ^{in}$ passes through $\Sigma ^{out}$ at a point whose distance to the set $\{(x,y,z+\rho )\; | \ (x,y,z)\in F\cap U\}$ is $O(\varepsilon ^{2/3})$.

• (ii) The map $\Pi$ is exponentially contracting in the $z$ direction. More precisely,

  $$\begin{aligned} \left\| \frac{\partial \Pi }{\partial z}\right\| =O(e^{-c/\varepsilon }), \end{aligned}$$

  where $c$ is a positive constant.

• (iii) The contraction/expansion of $\Pi$ in the direction of the fold is uniformly bounded; namely, if $v$ is the tangent vector to the fold at some point $(x,y,z)\in F\cap U$ then there exists a constant $K>0$ such that

  $$\begin{aligned} \frac{1}{K}\le \left| \mathrm{grad}\; \Pi (x,y,z)\cdot v \right| \le K. \end{aligned}$$

Remark 1

In [14], the statement of the fold Theorem (Theorem 1) is preceded by transformation to a “normal form,” which has the effect of straightening some of the manifolds. We have chosen to state the theorem without the preliminary transformation. Our result can be obtained by a combination of Theorem 1 of [14] and their result on the preliminary transformation.

We have purposely weakened the statement of item (iii) as the estimate we give is sufficient for the purposes of this article and the statement becomes simpler. We refer the reader to [14] for sharper estimates.

1.3 Folded Saddles

We use the notation and definition of the sections of the flow as in Sect. 8.2, as well as the hypotheses there, with one difference. Namely, we assume that (B) is violated, that is we assume

$$\begin{aligned} f(0,0,0,0)\cdot \mathrm{grad}\; g(0,0,0,0)=0. \end{aligned}$$

(61)

The defining condition for a folded saddle is stated using the desingularized Eq. (15) derived in Sect. 2.3. Note that condition (61) implies that $(0,0)$ is an equilibrium of (15). Then, $(0,0,0,0)$ is a folded saddle and $(0,0)$ is a saddle type equilibrium of (15). Further, a non-degeneracy condition is needed on the function

$$\begin{aligned} F_c(x,y,z,\varepsilon )=f(x,y,z,\varepsilon )\cdot g(x,y,z,\varepsilon ); \end{aligned}$$

namely, if $v$ is a tangent vector to the fold line $F$ at $(0,0,0,0)$ then

$$\begin{aligned} \mathrm{grad}\; F_c(0,0,0,0)\cdot v\ne 0. \end{aligned}$$

(62)

Note that, for $\rho$ sufficiently small, $\Sigma ^{in}$ is now naturally divided into the following two regions:

$$\begin{aligned}&\Sigma ^{in}_+ =\{(x,y,z)\in \Sigma ^{in}\; |\; F_c(x,y,z,\varepsilon )>0\}\quad \text{ and }\\&\Sigma ^{in}_- =\{(x,y,z)\in \Sigma ^{in}\; |\; F_c(x,y,z,\varepsilon )<0\} \end{aligned}$$

Then, we have the following theorem:

Theorem 8

(Folded saddle) [13, 14] For system (59) with the general assumptions (A) and (C), as well as (61) and (62), there exist $\varepsilon _0 >0$, a neighborhood $U$ of $(0,0,0)$, and open sets $U_1, U_2$ and $U_3$ such that the following assertions hold for $\varepsilon \in (0,\varepsilon _0]$:

• (i) $U=U_1\cup U_2\cup U_3, U_1\cap U_3=\emptyset , U_1\cup U_2\subset \Sigma ^{in}_+$ and $U_2$ is exponentially thin, i.e. there exists $c>0$ such that for every point $p\in U_2$ the length of the line segment $\{q\in U_2\; q=p+sv\quad \text{ for } \text{ some }\quad s\in \mathbb{R }\}$ is bounded by $e^{-c/\varepsilon }$.

• (ii) The transition map $\Pi : \Sigma ^{in}\cap U_1\rightarrow \Sigma ^{out}$ induced by the flow of (59) is a diffeomorphism mapping a neighborhood of $S_0\cap U$ into $\Sigma ^{out}$. Any trajectory starting at $S_{a,\varepsilon }\cap \Sigma ^{in}$ passes through $\Sigma ^{out}$ at a point whose distance to the set $\{(x,y,z+\rho )\; |\ (x,y,z)\in F\cap U\}$ is $O(\varepsilon ^{2/3})$.

• (iii) The map $\Pi$ is exponentially contracting in the $z$ direction. More precisely,

  $$\begin{aligned} \left\| \frac{\partial \Pi }{\partial z}\right\| =O(e^{-\tilde{c}/\varepsilon }), \end{aligned}$$

  where $\tilde{c}$ is a positive constant.

• (iv) The contraction/expansion of $\Pi$ in the direction of the fold is algebraic in $\varepsilon$, namely there exists a constant $\alpha >0$ such that if $v$ is the tangent vector to the fold at some point $(x,y,z)\in F\cap U$ then

  $$\begin{aligned} \varepsilon ^{\alpha }\le \left\| \hbox {grad}\; \Pi (x,y,z)\cdot v)\right\| \le \frac{1}{\varepsilon ^\alpha }. \end{aligned}$$

• (v) Trajectories starting in $U_2$ turn around before reaching $\Sigma ^{out}$ and return to $S_{a,\varepsilon }$.

The sets $U_1, U_2$ and $U_3$ are shown in Fig. 20.

Fig. 20

Dynamics in chart $K_\mathrm{ex}$

Sketch of the proof

Theorem 8 (or a similar version) is not stated in either [13] or [14], but it follows closely from the results and arguments given in these articles. In this article, we sketch the proof of the result, referring the reader to [13, 14]. Let $S_0$ be the critical manifold for (59) and let

$$\begin{aligned} S^a_0=\{(x,y,z)\in S_0\; |\; \frac{\partial g}{\partial z}(x,y,z,0)<0\} \end{aligned}$$

and

$$\begin{aligned} S^r_0=\{(x,y,z)\in S_0\; |\; \frac{\partial g}{\partial z}(x,y,z,0)>0\}. \end{aligned}$$

Removing a small neighborhood of the fold, we construct normally hyperbolic (Fenichel) slow manifolds $S^a_\varepsilon$ and $S^r_{\varepsilon }$. In [13], it is proved that for a fixed choice of the Fenichel manifolds $S^{a}_\varepsilon$ and $S^{r}_\varepsilon$ there exists a unique canard solution, i.e. a solution connecting from $S^a_\varepsilon$ to $S^{r}_\varepsilon$. The canard solution divides $S^a_\varepsilon$ into regions with two types of dynamics: on one side solutions pass to $\Sigma ^{out}$ and continue on along the fast direction and on the other side solutions return to $S^a_\varepsilon$. These regions correspond to $U_1$ and $U_3$. In between there is an exponentially thin region centered at the canard solution consisting of trajectories that follow $S^r_\varepsilon$ in a similar way as in classical canard phenomenon (canard explosion), see for example [11]. This region corresponds to $U_2$. We note that the flow in the direction of the fold line is more complicated due to the saddle structure, which accounts for the weaker version of statement (iii) in comparison to Theorem 7. $\square$