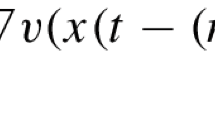Abstract
For a certain class of delay equations with piecewise constant nonlinearities we prove the existence of a rapidly oscillating stable periodic solution and a rapidly oscillating unstable periodic solution. Introducing an appropriate Poincaré map, the dynamics of the system may essentially be reduced to a two dimensional map, the periodic solutions being represented by a stable and a hyperbolic fixed point. We show that the two dimensional map admits a one dimensional invariant manifold containing the two fixed points. It follows that the delay equations under consideration admit a one parameter family of rapidly oscillating heteroclinic solutions connecting the rapidly oscillating unstable periodic solution with the rapidly oscillating stable periodic solution.
Similar content being viewed by others
References
Aschwanden A., Schulze-Halberg A., Stoffer D.: Stable periodic solutions for delay equations. Discrete Contin. Dyn. Syst. 14(4), 721–236 (2006)
Ivanov A.F., Losson J.: Stable rapidly oscillating solutions in delay differential equations with negative feedback. Diff. Integral Equat. 13, 811–832 (1999)
Krisztin, T., Walther, H.-O., Wu, J.: Shape, Smoothness and Invariant Stratification of an Attracting Set for Delayed Monotone Positive Feedback. Fields Institute Monographs, vol. 11. American Mathematical Society, Providence, RI (1999)
Mallet-Paret, J., Walther, H.-O.: Rapid oscillations are rare in scalar systems governed by monotone negative feedback with a time delay. Preprint (1994)
Nipp, K., Stoffer, D.: Invariant manifolds. In preparation
Rupflin, M.: Existenz schnellschwingender periodischer Lösungen bei steifen Differentialgleichungen mit konstanter Verzögerung. Diploma Thesis (2006). http://www.math.ethz.ch/~mrupflin/Diplomarbeit.pdf. Accessed 8 Aug 2008
Stoffer, D.: Delay equations with rapidly oscillating stable periodic solutions. J. Dynam. Diff. Equat. 20(1), 201–238 (2008)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Rupflin, M. Heteroclinic Connection of Periodic Solutions of Delay Differential Equations. J Dyn Diff Equat 21, 45–71 (2009). https://doi.org/10.1007/s10884-008-9123-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10884-008-9123-4