Skip to main content
SpringerLink
Log in

Hyperbolicity singularities in Rarefaction Waves

  • Published:
Journal of Dynamics and Differential Equations Aims and scope Submit manuscript

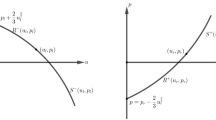
For mixed-type systems of conservation laws, rarefaction waves may contain states at the boundary of the elliptic region, where two characteristic speeds coincide, and the Lax family of the wave changes. Such contiguous rarefaction waves form a single fan with a continuous profile. Different pairs of families may appear in such rarefactions, giving rise to novel Riemann solution structures. We study the structure of such rarefaction waves near regular and exceptional points of the elliptic boundary and describe their effect on Riemann solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Anosov, D. V., and Arnold, V. I., eds. (1988). Dynamical Systems. I. Ordinary Differential Equations and Smooth Dynamical Systems. Springer, Berlin

    MATH  Google Scholar 

  2. Arnold V.I. (1983). Geometrical Methods in the Theory of Ordinary Differential Equations. Springer, New York

    MATH  Google Scholar 

  3. Azevedo, A. V., and Marchesin, D. (1990). Multiple viscous profile Riemann solutions in mixed elliptic-hyperbolic models for flow in porous media. In Nonlinear Evolution Equations that Change Type, IMA Vol. Math. Appl. 27, Springer, New York.

  4. Azevedo A.V., Marchesin D., Plohr B. and Zumbrun K. (2002). Capillary instability in models for three-phase flow. Angew, Z.,. Math. Phys. 53: 713–746

    Article  MATH  MathSciNet  Google Scholar 

  5. Bell J.B., Trangenstein J.A. and Shubin G.R. (1986). Conservation laws of mixed type describing three-phase flow in porous media. SIAM J. Appl. Math. 46: 1000–1017

    Article  MATH  MathSciNet  Google Scholar 

  6. Dara L. (1975). Singularités génériques des équations différentielles multiformes. Bol. Soc. Brasil. Mat. 6: 95–128

    Article  MATH  MathSciNet  Google Scholar 

  7. Eschenazi C. (1995). Rarefaction fields in systems of three conservation laws. Mat. Contemp. 8: 151–176

    MATH  MathSciNet  Google Scholar 

  8. Eschenazi C. and Palmeira C.F.B. (1998). Local topology of elementary waves for systems of two conservation laws. Mat. Contemp. 15: 127–144

    MATH  MathSciNet  Google Scholar 

  9. Isaacson E.L., Marchesin D., Palmeira C.F. and Plohr B.J. (1992). A global formalism for nonlinear waves in conservation laws. Comm. Math. Phys. 146: 505–552

    Article  MATH  MathSciNet  Google Scholar 

  10. Isaacson E.L., Marchesin D. and Plohr B.J. (1990). Transitional waves for conservation laws. SIAM J. Math. Anal. 21: 837–866

    Article  MATH  MathSciNet  Google Scholar 

  11. Keyfitz B.L. (1995). A geometric theory of conservation laws which change type. Z. Angew. Math. Mech. 75: 571–581

    MATH  MathSciNet  Google Scholar 

  12. Mailybaev A.A. (2000). Transformation of families of matrices to normal forms and its application to stability theory. SIAM J. Matrix Anal. Appl. 21: 396–417

    Article  MathSciNet  Google Scholar 

  13. Mailybaev A.A. (2001). Transformation to versal deformations of matrices. Linear Algebra Appl. 337: 87–108

    Article  MATH  MathSciNet  Google Scholar 

  14. Marchesin D. and Palmeira C.F.B. (1994). Topology of elementary waves for mixed-type systems of conservation laws. J. Dynam. Differ. Eq. 6: 427–446

    Article  MATH  MathSciNet  Google Scholar 

  15. Marchesin D. and Plohr B. (2001). Wave structure in WAG recovery. Soc. Petroleum Eng. J, 6: 209–219

    Google Scholar 

  16. Matos, V. M. M. (2004). Riemann Problem for Two Conservation Laws of Type IV with Elliptic Region, Ph.D. Thesis, IMPA, Riode Janeiro (in Portuguese).

  17. Palmeira, C. F. B. (1988). Line fields defined by eigenspaces of derivatives of maps from the plane to itself, Proceedings of the Sixth International Colloquium on Differential Geometry (Santiago de Compostela), pp 177–205.

  18. Pego L.R. and Serre D. (1988). Instabilities in Glimm’s scheme for two systems of mixed type. SIAM J. Numer. Anal. 25: 965–988

    Article  MATH  MathSciNet  Google Scholar 

  19. Radicchi, R. (2005). On implicit ordinary differential equations in three dimensions, Ph.D Thesis, Universidade Federal de Minas Gerais, Minas Gerais (Brazil).

  20. Schaeffer D.G. and Shearer M. (1987). The classification of 2 ×  2 systems of nonstrictly hyperbolic conservation laws, with application to oil recovery. Comm. Pure Appl. Math. 40: 141–178

    Article  MATH  MathSciNet  Google Scholar 

  21. Schaeffer D.G. and Shearer M. (1987). Riemann problems for nonstrictly hyperbolic 2 × 2 systems of conservation laws. Trans. Amer. Math. Soc. 304: 267–306

    Article  MATH  MathSciNet  Google Scholar 

  22. Schecter S., Plohr B.J. and Marchesin D. (2001). Classification of codimension-one Riemann solutions. J. Dynam. Differ. Eq. 13: 523–588

    Article  MATH  MathSciNet  Google Scholar 

  23. Schulte W. and Falls A. (1992). Features of three-component, three-phase displacement in porous media. SPE Reservoir Eng. 7: 426–432

    Google Scholar 

  24. Seyranian A.P. and Mailybaev A.A. (2003). Multiparameter Stability Theory with Mechanical Applications. World Scientific, Singapore

    MATH  Google Scholar 

  25. Shearer M. and Trangenstein J. (1989). Loss of Real Characteristics for Models of Three-Phase Flow in Porous Media. Transport in Porous Media. 4: 499–525

    Article  Google Scholar 

  26. Smoller J. (1983). Shock Waves and Reaction-Diffusion Equations. Springer, New York

    MATH  Google Scholar 

  27. Tang Z.J. and Ting T.C.T. (1987). Wave curves for the Riemann problem of plane waves in isotropic elastic solids, Internat. J. Engrg. Sci. 25: 1343–1381

    Article  MATH  MathSciNet  Google Scholar 

  28. Xin Z.P. (1989). Asymptotic stability of rarefaction waves for 2 × 2 viscous hyperbolic conservation laws—the two-modes case. J. Differ. Eq. 78: 191–219

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Mechanics, Moscow State Lomonosov University, Michurinsky pr. 1, 119192, Moscow, Russia

    Alexei A. Mailybaev

  2. Instituto Nacional de Matemática Pura e Aplicada – IMPA, Estrada Dona Castorina, 110, 22460-320, Rio de Janeiro, RJ, Brazil

    Dan Marchesin

Authors
  1. Alexei A. Mailybaev
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dan Marchesin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alexei A. Mailybaev.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mailybaev, A.A., Marchesin, D. Hyperbolicity singularities in Rarefaction Waves. J Dyn Diff Equat 20, 1–29 (2008). https://doi.org/10.1007/s10884-007-9070-5

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10884-007-9070-5

Keywords

Search

Navigation