Stabilization of One-Dimensional Schrödinger Equation Under Joint Feedback Control with Delayed Observation

Abstract

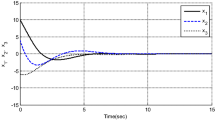
In this paper, we consider a one-dimensional Schrödinger equation under a joint linear feedback control at an arbitrary internal point $\xi (0<\xi <1)$. It is shown that the pointwise control system is asymptotically stable if $\xi$ is either an irrational number or a rational number satisfying $\xi \neq 2l/(2m-1)$ for any positive integers $l, m (1\leq l \leq m-1)$; further, the system is exponentially stable if $\xi$ is a rational number satisfying $\xi \neq 2l/(2m-1)$ for any positive integers $l, m (1\leq l \leq m-1)$. Moreover, we consider the Schrödinger equation under a joint feedback control where the observation is suffered from a given time delay. A Luenberger observer is designed at the time interval when the observation signal is available, while a predictor is designed at the time interval when the observation signal is not available. A natural control law is constructed based on the estimated state. The closed-loop system is shown to be exponentially stable for the smooth initial value. Finally, numerical simulations demonstrate effectiveness of the dynamic output feedback controller.