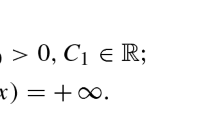Skip to main content
SpringerLink
Log in

Hierarchical Control for the One-dimensional Plate Equation with a Moving Boundary

  • Published:
Journal of Dynamical and Control Systems Aims and scope Submit manuscript

A Correction to this article was published on 22 August 2018

This article has been updated

Abstract

In this paper, we investigate the controllability for the one-dimensional plate equation in intervals with a moving boundary. This equation models the vertical displacement of a point x at time t in a bar with uniform cross section. We assume the ends of the bar with small and uniform variations. More precisely, we have introduced functions α(t) and β(t) modeling the motion of these ends. We present the following results: the existence and uniqueness of Nash equilibrium, the approximate controllability with respect to the leader control, and the optimality system for the leader control.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

Change history

References

  1. Nash J. Noncooperative games. Ann Math 1951;54:286–295.

    Article  MathSciNet  MATH  Google Scholar 

  2. Pareto V. Cours d’économie politique. Switzerland: Rouge; 1896.

    Google Scholar 

  3. Stackelberg H. Marktform Und gleichgewicht. Berlin: Springer; 1934.

    Google Scholar 

  4. Lions J-L. Hierarchic control. Math Sci Proc Indian Acad Sci 1994;104:295–304.

    Article  MathSciNet  MATH  Google Scholar 

  5. Jesus I. Hierarchical control for the wave equation with a moving boundary. J Optim Theory Appl 2016;171:336–350.

    Article  MathSciNet  MATH  Google Scholar 

  6. Hörmander L, Vol. 116. Linear partial differential operators Die Grundlehren der mathematischen Wissenschaften Bd. New York: Academic Press Inc., Publishers; 1963.

    Google Scholar 

  7. Lions J-L. Contrôle de Pareto de systèmes distribués. Le cas d’ évolution. CR Acad Sc Paris, Sér I 1986;302(11):413–417.

    MATH  Google Scholar 

  8. Lions J-L. Some remarks on Stackelberg’s optimization. Math Models Methods Appl Sci 1994;4:477–487.

    Article  MathSciNet  MATH  Google Scholar 

  9. Díaz J, Lions J-L. On the approximate controllability of Stackelberg-Nash strategies. Ocean circulation and pollution control mathematical and numerical investigations. In: Díaz JI, editors. Berlin: Springer; 2005. p. 17–27.

  10. Díaz J. On the von Neumann problem and the approximate controllability of Stackelberg-Nash strategies for some environmental problems. Rev R Acad Cien, Ser A Math 2002;96(3):343–356.

    MathSciNet  MATH  Google Scholar 

  11. Glowinski R, Ramos A, Periaux J. Nash equilibria for the multi-objective control of linear differential equations. J Optim Theory Appl 2002;112(3):457–498.

    Article  MathSciNet  MATH  Google Scholar 

  12. Glowinski R, Ramos A, Periaux J. Pointwise control of the Burgers equation and related Nash equilibrium problems: computational approach. J Optim Theory Appl 2002;112(3):499–516.

    Article  MathSciNet  MATH  Google Scholar 

  13. González G, Lopes F, Rojas-Medar M. On the approximate controllability of Stackelberg-Nash strategies for Stokes equations. Proc Amer Math Soc 2013;141(5): 1759–1773.

    Article  MathSciNet  MATH  Google Scholar 

  14. Limaco J, Clark H, Medeiros LA. Remarks on hierarchic control. J Math Anal Appl 2009;359:368–383.

    Article  MathSciNet  MATH  Google Scholar 

  15. Araruna FD, Fernández-Cara E, Santos M. Stackelberg-Nash exact controllability for linear and semilinear parabolic equations, ESAIM : Control. Optim Calc Var 2015;21(3):835–856.

    Article  MathSciNet  MATH  Google Scholar 

  16. Araruna FD, Fernández-cara E, Guerrero S, Santos M. New results on the Stackelberg-Nash exact control of linear parabolic equations. Syst Control Lett 2017; 104:78–85.

    Article  MathSciNet  MATH  Google Scholar 

  17. Ramos A, Roubicek T. Nash equilibria in noncooperative Predator-Prey games. Appl Math Optim 2007;56(2):211–241.

    Article  MathSciNet  MATH  Google Scholar 

  18. Araruna FD, Antunes GO, Medeiros LA. Exact controllability for the semilinear string equation in non cylindrical domains. Control Cybern 2004;33:237–257.

    MathSciNet  MATH  Google Scholar 

  19. Cui L, Song L. 2014. Exact controllability for a wave equation with fixed boundary control. Boundary Value Problems. https://doi.org/10.1186/1687-2770-2014-47.

  20. Bardos C, Chen G. Control and stabilization for the wave equation. Part III: domain with moving boundary. SIAM J Control Optim 1981;19:123–138.

    Article  MathSciNet  MATH  Google Scholar 

  21. Cui L, Liu X, Gao H. Exact controllability for a one-dimensional wave equation in non-cylindrical domains. J Math Anal Appl 2013;402:612–625.

    Article  MathSciNet  MATH  Google Scholar 

  22. Milla Miranda M. Exact controlllability for the wave equation in domains with variable boundary. Rev Mat Univ Complut Madr 1996;9:435–457.

    MathSciNet  MATH  Google Scholar 

  23. Milla Miranda M. HUM and the wave equation with variable coefficients. Asymptot Anal 1995;11:317–341.

    MathSciNet  MATH  Google Scholar 

  24. Jesus I. Approximate controllability for a one-dimensional wave equation with the fixed endpoint control. J Differ Equ 2017;263:5175–5188.

    Article  MathSciNet  Google Scholar 

  25. Caldas C, Limaco J, Barreto R, Gamboa P. Exact controllability for the equation of the one dimensional plate in domains with moving boundary. Divulg Mat 2003;11:19–38.

    MathSciNet  MATH  Google Scholar 

  26. Aubin J. L’analyse non linéaire et ses Motivations Économiques. Paris: Masson; 1984.

    MATH  Google Scholar 

  27. Lions J-L. Contrôle optimal des systèmes gouvernés par des équations aux dérivées partielles. Paris: Dunod; 1968.

    MATH  Google Scholar 

  28. Rockafellar R. Convex Analysis. Princeton: Princeton University Press; 1969.

    Google Scholar 

  29. Brezis H. Functional analysis, Sobolev spaces and partial differential equations. Berlin: Springer-Verlag; 2010.

    Book  Google Scholar 

  30. Ekeland I, Temam R. analyse convexe et problèmes variationnels. Paris: Dunod, Gauthier-Villars; 1974.

    MATH  Google Scholar 

Download references

Acknowledgments

We would like to thank the professor L. A. Medeiros by gentle suggestion of this problem and also to professor Marcos Travaglia for his comments on the manuscript. Moreover, the authors are grateful to the anonymous referees for their constructive comments and suggestions, which helped in improving the original manuscript significantly.

Author information

Authors and Affiliations

  1. Universidade Federal do Piauí, DM, Teresina, PI, Brazil

    I. P. de Jesus & M. R. Clark

  2. Universidade Federal Fluminense, IME, Niterói, RJ, Brazil

    J. Limaco

Authors
  1. I. P. de Jesus
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. Limaco
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. R. Clark
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to I. P. de Jesus.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

de Jesus, I.P., Limaco, J. & Clark, M.R. Hierarchical Control for the One-dimensional Plate Equation with a Moving Boundary. J Dyn Control Syst 24, 635–655 (2018). https://doi.org/10.1007/s10883-018-9413-z

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10883-018-9413-z

Keywords

Mathematics Subject Classification (2010)

Search

Navigation