Abstract
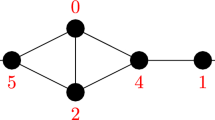
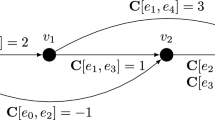
We study the maximum flow problem subject to binary disjunctive constraints in a directed graph: A negative disjunctive constraint states that a certain pair of arcs in a digraph cannot be simultaneously used for sending flow in a feasible solution. In contrast to this, positive disjunctive constraints force that for certain pairs of arcs at least one arc has to carry flow in a feasible solution. It is convenient to represent the negative disjunctive constraints in terms of a so-called conflict graph whose vertices correspond to the arcs of the underlying graph, and whose edges encode the constraints. Analogously we represent the positive disjunctive constraints by a so-called forcing graph.
For conflict graphs we prove that the maximum flow problem is strongly \(\mathcal{NP}\)-hard, even if the conflict graph consists only of unconnected edges. This result still holds if the network consists only of disjoint paths of length three. For forcing graphs we also provide a sharp line between polynomially solvable and strongly \(\mathcal{NP}\)-hard instances for the case where the flow values are required to be integral. Moreover, our hardness results imply that no polynomial time approximation algorithm can exist for both problems. In contrast to this we show that the maximum flow problem with a forcing graph can be solved efficiently if fractional flow values are allowed.


Similar content being viewed by others
Notes
A preliminary, short version of this paper appeared as Pferschy and Schauer (2011).
References
Ahuja RK, Magnanti TL, Orlin JB (1993) Network flows: theory, algorithms, and applications. Prentice Hall, New York
Ausiello G, Protasi M, Marchetti-Spaccamela A, Gambosi G, Crescenzi P, Kann V (1999) Complexity and approximation: combinatorial optimization problems and their approximability properties. Springer, Berlin
Bodlaender HL, Jansen K (1993) On the complexity of scheduling incompatible jobs with unit-times. In: MFCS ’93: proceedings of the 18th international symposium on mathematical foundations of computer science. Springer, Berlin, pp 291–300
Darmann A, Pferschy U, Schauer J, Woeginger GJ (2011) Paths, trees and matchings under disjunctive constraints. Discrete Appl Math 159(16):1726–1735
Garey MR, Johnson DS (1979) Computers and intractability: a guide to the theory of NP-completeness. Freeman, New York
Goossens DR, Spieksma FCR (2009) The transportation problem with exclusionary side constraints. 4OR 7(1):51–60
Gusfield D, Naor D (1990) Efficient algorithms for generalized cut trees. In: SODA ’90: proceedings of the first annual ACM-SIAM symposium on discrete algorithms. SIAM, Philadelphia, pp 422–433
Hamacher HW, Picard J-C, Queyranne M (1984) Ranking the cuts and cut-sets of a network. Ann Discrete Math 19:183–200
Jansen K (1999) An approximation scheme for bin packing with conflicts. J Comb Optim 3:363–377
Jansen K, Öhring S (1997) Approximation algorithms for time constrained scheduling. Inf Comput 132(2):85–108
Papadimitriou CH, Yannakakis M (1991) Optimization, approximation, and complexity classes. J Comput Syst Sci 43(3):425–440
Pferschy U, Schauer J (2009) The knapsack problem with conflict graphs. J Graph Algorithms Appl 13(2):233–249
Pferschy U, Schauer J (2011) The maximum flow problem with conflict and forcing conditions. In: INOC. Lecture notes in computer science, vol 6701. Springer, Berlin, pp 289–294
Picard J-C, Queyranne M (1980) On the structure of all minimum cuts in a network and applications. Math Program Stud 13:8–16
Zhang R, Kabadi SN, Punnen AP (2011) The minimum spanning tree problem with conflict constraints and its variations. Discrete Optim 8(2):191–205
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Pferschy, U., Schauer, J. The maximum flow problem with disjunctive constraints. J Comb Optim 26, 109–119 (2013). https://doi.org/10.1007/s10878-011-9438-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10878-011-9438-7